ЛАБОРАТОРНЫЙ ПРАКТИКУМ К ГЛАВЕ 3
Лабораторная работа 3.1.
Решение системы линейных алгебраических уравнений
методом Гаусса
Задание.
Решить СЛАУ методом Гаусса.
Варианты задания.
где
– номер факультета;
– номер группы;
– номер студента по журналу.
Пример выполнения лабораторной работы.
Дана система уравнений
Ручной счет.
Расширенная матрица системы имеет вид:
.
Выполним прямой ход метода Гаусса.
На первом шаге прямого хода из второй
строки вычитаем первую, умноженную на
коэффициент
,
а из третьей строки вычитаем первую,
умноженную на
.
В результате после первого шага будем
иметь:
.
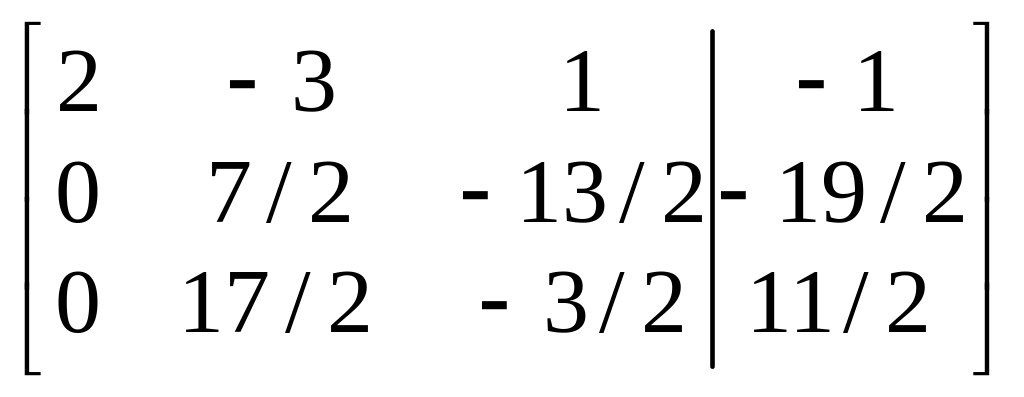На втором шаге прямого хода из третьей
строки вычитаем вторую, умноженную на
.
В результате после второго шага будем
иметь:
.
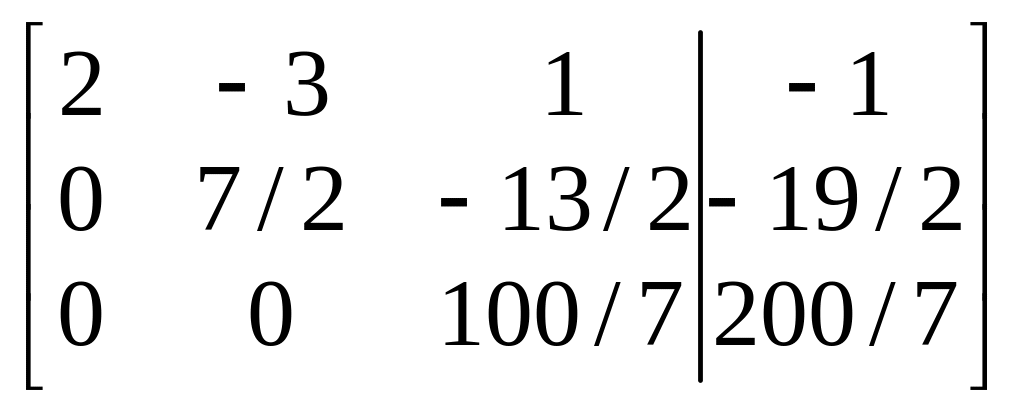Выполним теперь обратный ход метода Гаусса.
Эквивалентная система с треугольной матрицей может быть записана следующим образом:
Из третьего уравнения находим:
.
Из второго уравнения находим:
.
Из первого уравнения находим:
.
Итак, решение рассматриваемой СЛАУ следующее:
.
Выполнение работы на ЭВМ.
Пример программы на Фортране:
program lab_3_1 ! Требуется подключить файл integer(4), parameter :: n=3 ! simq.for, содержащий real(4), dimension(n,n) :: A,b(n) ! подпрограмму SIMQ из integer(4) :: i,j,ier ! математической библиотеки SSP print *,’ Vvedite matritsu A i vector b’ read *,((A(i,j),j=1,n),b(i),i=1,n) print *,’ Iskhodnaya systema’ do i=1,n print 1,(A(i,j),j=1,n),b(i) end do 1 format(10f8.2) call SIMQ(A,b,n,ier) print *,’ Kod oshibki ier=’,ier print 2,b 2 format(8x,’Reshenie’/10f8.2) end |
К программе необходимо подключить стандартную подпрограмму SIMQ.
Результаты расчета:
Iskhodnaya systema
2.00 -3.00 1.00 -1.00
1.00 2.00 -6.00 -10.00
5.00 1.00 1.00 3.00
Kod oshibki ier= 0
Reshenie
0.00 1.00 2.00
Коэффициенты системы вводятся строками расширенной матрицы.
Лабораторная работа 3.2. Вычисление обратной матрицы и определителя методом Гаусса
Задание.
Для заданной матрицы
вычислить обратную матрицу и определитель.
Варианты задания.
,
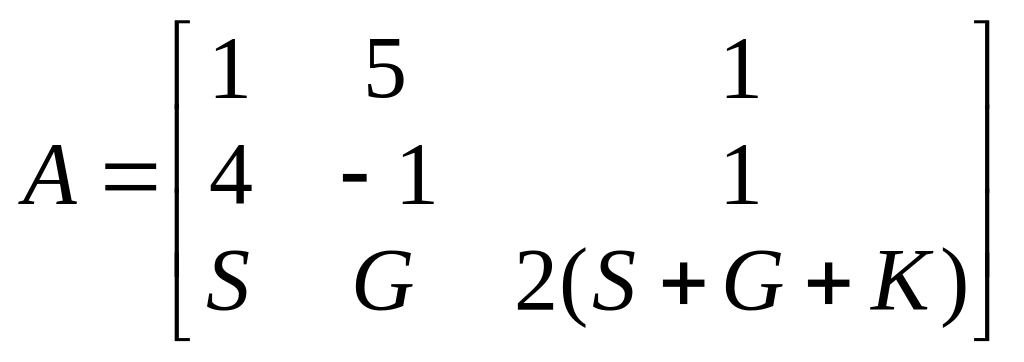где – номер факультета; – номер группы; – номер студента по журналу.
Пример выполнения лабораторной работы.
Пусть задана матрица
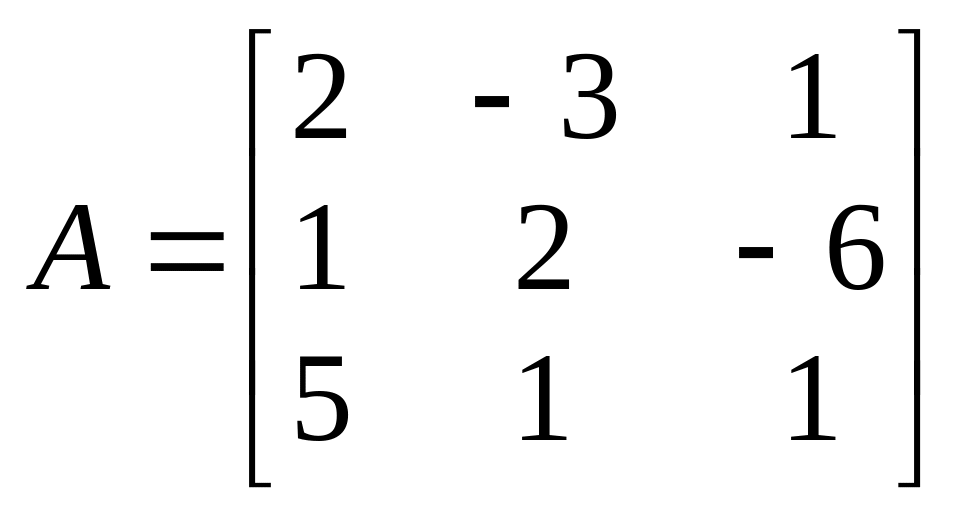
Ручной счет.
Соответствующая расширенная матрица:
.
Выполним прямой ход метода Гаусса по всей расширенной матрице.
После первого шага получим:
.
После второго шага получим:
.
Вычисляем определитель матрицы:
.
Для вычисления элементов обратной матрицы выполним теперь обратный ход по каждой правой части расширенной матрицы.
Вычисляем элементы первого столбца обратной матрицы:
– из третьего уравнения
;
– из второго уравнения
;
– из первого уравнения
.
Вычисляем элементы второго столбца обратной матрицы:
– из третьего уравнения
;
– из второго уравнения
;
– из первого уравнения
.
Вычисляем элементы третьего столбца обратной матрицы:
– из третьего уравнения
;
– из второго уравнения
;
– из первого уравнения
.
Итак, искомая обратная матрица имеет вид:
.
Выполнение работы на ЭВМ.
Пример программы на Фортране:
program lab_3_2 ! Требуется подключить файл integer(4), parameter :: n=3 ! minv.for, содержащий real(4), dimension(n,n) :: A ! подпрограмму MINV из integer(4), dimension(n) :: l,m ! математической библиотеки SSP real(4) :: d integer(4) :: i,j print*,’ Vvedite matritsu A’ read *,((A(i,j),j=1,n),i=1,n) print *,’ Iskhodnaya matritsa’ do i=1,n print 1,(A(i,j),j=1,n) end do 1 format(10f8.4) call MINV(A,n,D,L,M) print *,’ Obratnaya matritsa’ do i=1,n print 1,(A(i,j),j=1,n) end do print 2,D 2 format(8x,’Opredelitel matritsi D=’,f8.2) end |
К программе необходимо подключить стандартную подпрограмму MINV.
Результаты расчета:
Iskhodnaya matritsa
2.00 -3.00 1.00
1.00 2.00 -6.00
5.00 1.00 1.00
Obratnaya matritsa
0.08 0.04 0.16
-0.31 -0.03 0.13
-0.09 -0.17 0.07
Opredelitel matritsi D= 100.00
Лабораторная работа 3.3. Решение систем линейных алгебраических уравнений итерационными методами
Задание.
1. Для заданной СЛАУ сделать 3 шага по итерационным схемам ме-
тодов простой итерации и Зейделя.
2. Решить СЛАУ на ЭВМ методом простой итерации и/или методом Зейделя (по указанию преподавателя).
Варианты задания.
где – номер факультета; – номер группы; – номер студента по журналу.
Пример выполнения лабораторной работы.
Дана система уравнений
Выполним проверку выполнения достаточного условия сходимости.
Проверяем условие диагонального преобладания.
первое уравнение: 4>1+1=2 – выполняется;
второе уравнение: 2<1+5=6 – не выполняется;
третье уравнение: |–1|<1+6=7 – не выполняется.
Таким образом, условие диагонального преобладания для исходной системы уравнений не выполняется и поэтому не может быть гарантирована сходимость итерационных методов к решению. Для данной системы можно добиться выполнения этого условия перестановкой второго и третьего уравнений:
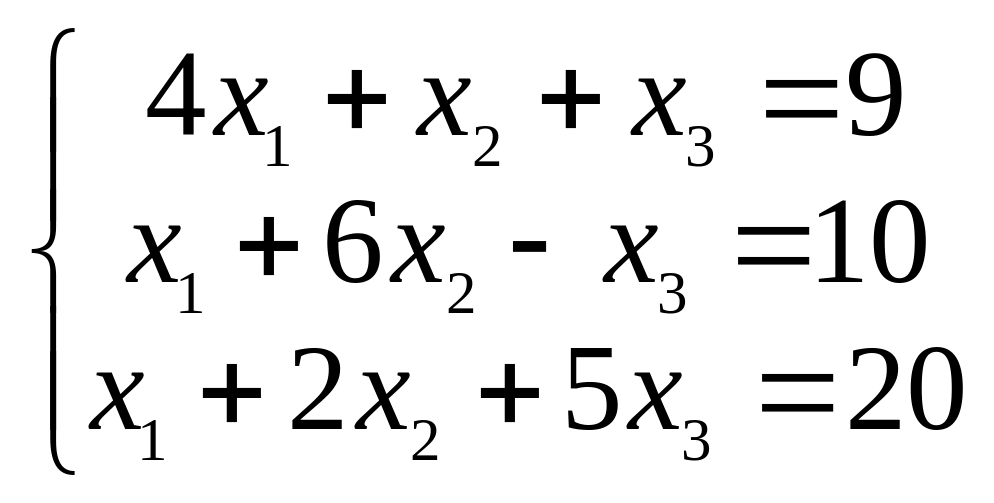
Проверяем условие диагонального преобладания для преобразованной системы:
первое уравнение: 4>1+1=2 – выполняется;
второе уравнение: 6>1+|–1|=2 – выполняется;
третье уравнение: 5>1+2=3 – выполняется.
Ручной счет.