7. Полярная система координат. Построениие линии в полярной системе координат

Полярная система координат на плоскости задаётся точкой О, называемой полюсом, и направленной прямой Ох, называемой полярной осью. С каждой точкой Р плоскости, на которой задана полярная система координат, можно связать определённую пару чисел r, φ (полярные координаты). Полярный радиус r есть длина отрезка ОР, а полярный угол φ – радианная мера угла хОР, отсчитанного в направлении, противоположном вращению часовой стрелки (рис. 7.1) (в противном случае угол считается отрицательным).

Рис. 7.1

Угол φ определён с точностью до слагаемого 2kπ, где k –любое целое число. Точка (r; φ) по определению совпадает с точкой (–r; ± π): это условие связывает определённую точку плоскости с каждой парой чисел (r; φ) не только при положительных, но и при отрицательных значениях r. Для полюса О величина φ не определена.

Если полюс и полярная ось совпадают, соответственно, с началом О и осью Ох прямоугольной системы координат (рис 7.1), то при условии, что для измерения r, х, у использованы равные единицы масштаба, от прямоугольной системы координат можно перейти к полярным и наоборот. Переход от полярных координат к прямоугольной системы осуществляется по следующим формулам:

(7.1)

Если необходимо от прямоугольной системы перейти к полярным координатам, то следует использовать преобразования:

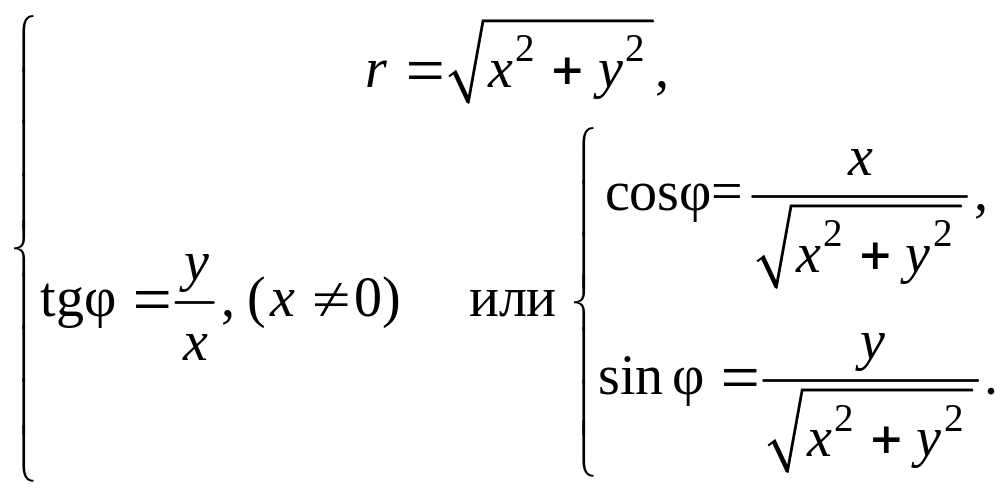(7.2)

Пример 1. Построить точки, заданные полярными координатами: А (3; π/4), В (2; 3π/4), С (–3; π/4), D (1; –π/4), Е (–4; π/3).

Решение. Выполним построения (рис 7.2)

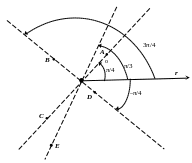
Рис. 7.2

Пример 2. Определить, какую линию представляет уравнение r = 2 sinφ.

Решение. Переходя к прямоугольной системе координат, по формулам (7.2) имеем

то есть или .

Таким образом, данное уравнение представляет окружность радиуса 1 с центром в точке С (0; 1) (рис. 7.3), проходящую через полюс О и касающуюся полярной оси Ох.

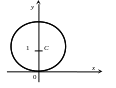
Рис.7.3.

Пример 3. Линия задана уравнением r = r(φ) в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от φ = 0 до φ = 2π и придавая φ значения через промежутки π/8; 2) найти уравнение данной линии в прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью; 3) по уравнению в прямоугольной системе координат определить, какая это линия.

а) ; б) .

Решение. а) Используя калькулятор, составим таблицу значений функции r (вычисления выполняем с двумя знаками после запятой):

φ	r	φ	r	φ	r
0 π/8 π/4 3π/8 π/2 5π/8	∞ 13,14 3,41 1,62 1 0,72	3π/4 7π/8 π 9π/8 5π/4 11π/8	0,59 0,52 0,5 0,52 0,59 0,72	3π/2 13π/8 7π/4 15π/8 2π	1 1,62 3,41 13,14 ∞

По данным точкам построим линию (рис. 7.4).

Рис. 7.4

По формулам (7.2) найдём уравнение линии в системе хОу:

.

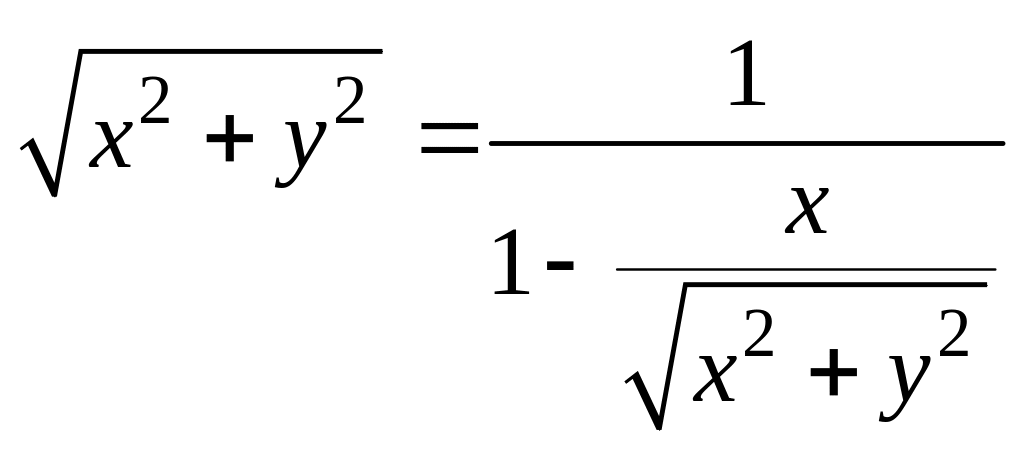Упростив последнее выражение, придём к уравнению

– х –1 = 0

Решив полученное иррациональное уравнение, имеем у² = 2( х + 1/2).

Уравнение у² = 2( х +1/2) в декартовой системе координат определяет параболу, симметричную относительно оси Ох с вершиной в точке у = 0, x = –1/2.

б) Составим таблицу значений функции r (вычисления выполняем с двумя знаками после запятой):

φ	cos φ	r	φ	cos φ	r
0	1	–5	9π/8	–0,92	0,75
π/8	0,92	–7,19	5π/4	–0,71	0,86
π/4	0,71	29,14	11π/8	–0,38	1,10
3π/8	0,38	3,40	3π/2	0	1,67
π/2	0	1,67	13π/8	0,38	3,40
5π/8	–0,38	1,10	7π/4	0,71	29,14
3π/4	–0,71	0,86	15π/8	0,92	–7,19
7π/8	–0,92	0,75	2π	1	–5
π	–1	0,71

По данным точкам построим линию (рис.7.5):

Рис 7.5

Уравнение линии задано формулой

,

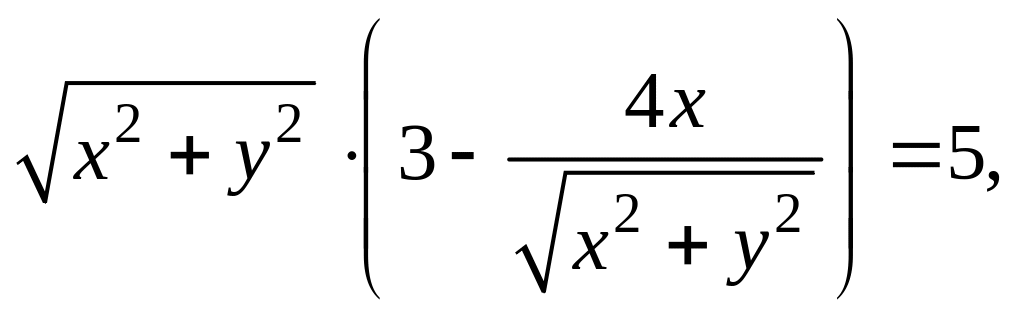
Решаем иррациональное уравнение:

9∙(x² + y² )= 25 +40x +16x²,

9x² + 9y² –40x –16x² = 25.

Приведем уравнение линии к каноническому виду

9y² –7x² –40x = 25,

,

Разделим обе части уравнения на , получим

.

Последнее уравнение в декартовой системе координат определяет гиперболу с полуосями;

Данный пример может быть использован при решении номеров 41 – 50 контрольной работы № 1.