3. Обратная матрица. Ранг матрицы

Квадратная матрица А называется невырожденной, если ее определитель не равен нулю. Если же det A = 0, то матрица А называется вырожденной.

Понятие обратной матрицы вводится только для квадратных невырожденных матриц.

Матрица А^–1 называется обратной для квадратной матрицы А порядка n, если А^–1 ·А = А ·А^–1 = E, где Е – единичная матрица порядка n.

Теорема. Для того чтобы существовала обратная матрица А^–1, необходимо и достаточно, чтобы матрица А была невырожденной.

Для любой невырожденной матрицы существует единственная обратная матрица, которую находят по формуле:

А^–1 = (3.1)

Пример 1. Дана матрица

.

Убедиться, что она невырожденная, найти обратную ей матрицу и проверить выполнение равенств

А·А^–1 = А^–1·А = E.

Решение. Вычислим определитель второго порядка:

|А| = = 3 + 8 = 11 ≠ 0,

следовательно, матрица А невырожденная и имеет обратную матрицу. Формула (3.1) для квадратной матрицы второго порядка имеет вид:

А^–1 = .

Найдем алгебраические дополнения для каждого элемента данной матрицы А:

А₁₁ = (–1)¹⁺¹ M₁₁ = а₂₂ = 1; А₂₁ = (–1)²⁺¹ M₂₁ = –a₁₂ = 4;

А₁₂ = (–1)¹⁺² M₁₂ = – а₂₁ = – 2; А₂₂ = (–1)²⁺² M₂₂ = a₁₁= 3.

Обратная матрица примет вид:

А^–1 = .

Выполним проверку:

А^–1 ·А =

= E.

Пример 2. Найти обратную матрицу для заданной матрицы:

B = .

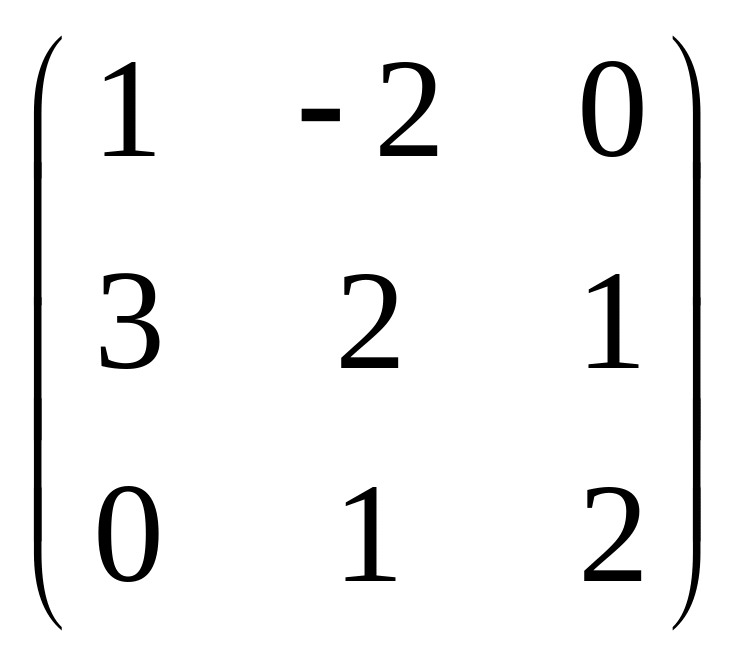Решение. Вычислим определитель матрицы B:

det B =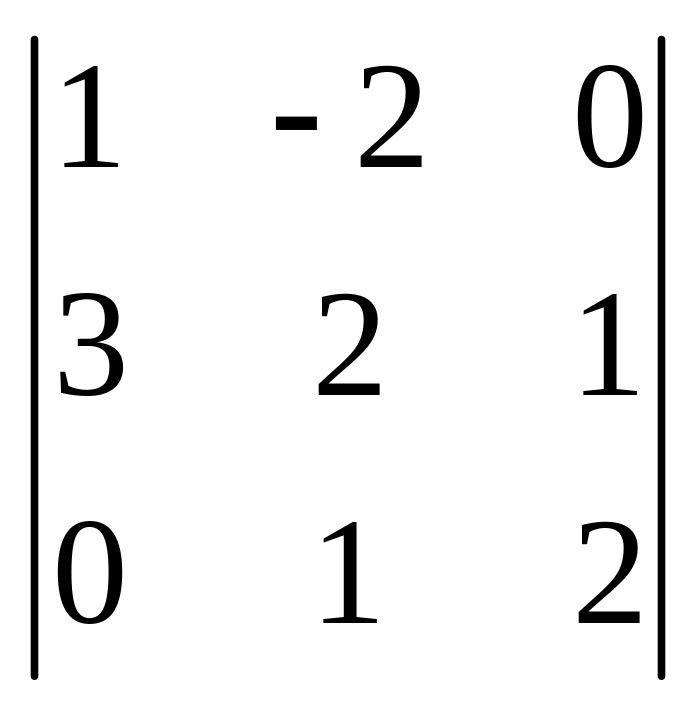 = 4 + 0 – 0 – 0 – 1 + 12 = 15 ≠ 0,

следовательно, матрица B^–1 существует. Формулу (3.1) для квадратной матрицы третьего порядка перепишем в виде

B^–1 = .

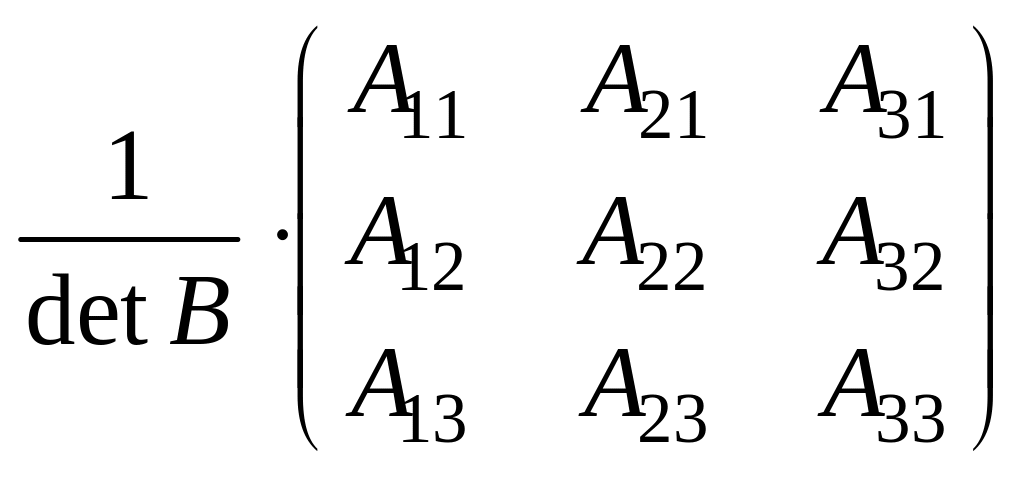Найдем алгебраические дополнения А _ij элементов b_ij матрицы B:

A₁₁ = (–1)¹⁺¹· = 3; А₂₁ = = 4; А₃₁ = = –2;

А₁₂ = (–1)¹⁺² = – 6; А₂₂ = = 2; А₃₂ = = –1;

А₁₃ = (–1)¹⁺³· = 3; А₂₃ = = – 1; А₃₃ = = 8.

Обратная матрица запишется так:

B^–1 = .

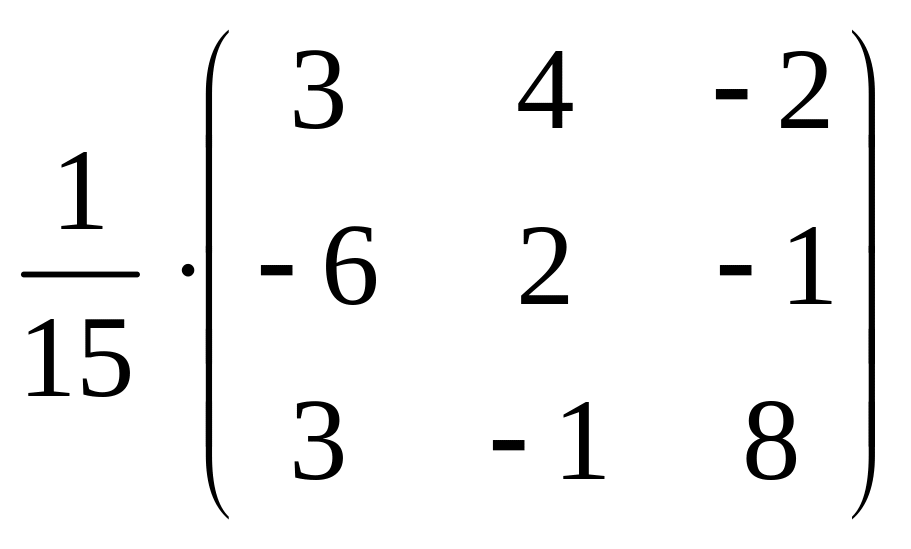Выполним проверку:

B^–1 ·B =

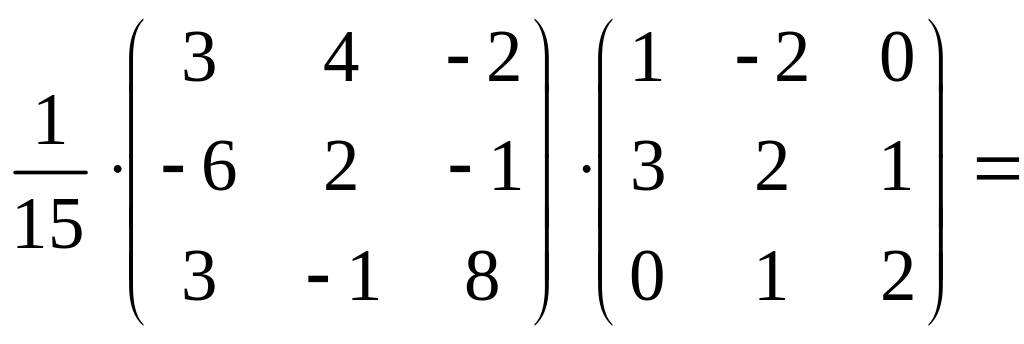
= E.

Рассмотрим матрицу А произвольной размерности m×n. Выделим в ней k строк и k столбцов, где k ≤ min(m,n). Элементы, стоящие на пересечении выделенных строк и столбцов, образуют квадратную матрицу порядка k. Определитель этой матрицы называется минором k-того порядка матрицы А.

Рангом матрицы называется наибольший из порядков миноров данной матрицы, отличный от нуля. Обозначается rang A, r(А).

Элементарными преобразованиями матрицы А называются:

1) перестановка местами двух строк или столбцов матрицы;

2) умножение каждого элемента строки (столбца) на число, отличное от нуля;

3) сложение элементов строки (столбца) с соответствующими элементами другой строки (столбца), умноженными на одно и то же произвольное число.

Элементарные преобразования не изменяют ранг матрицы. Значит, при его нахождении целесообразно провести такие преобразования над строками или столбцами матрицы, которые бы привели к матрице В, ранг которой найти просто. К таким матрицам относятся трапециевидные матрицы:

В = ,

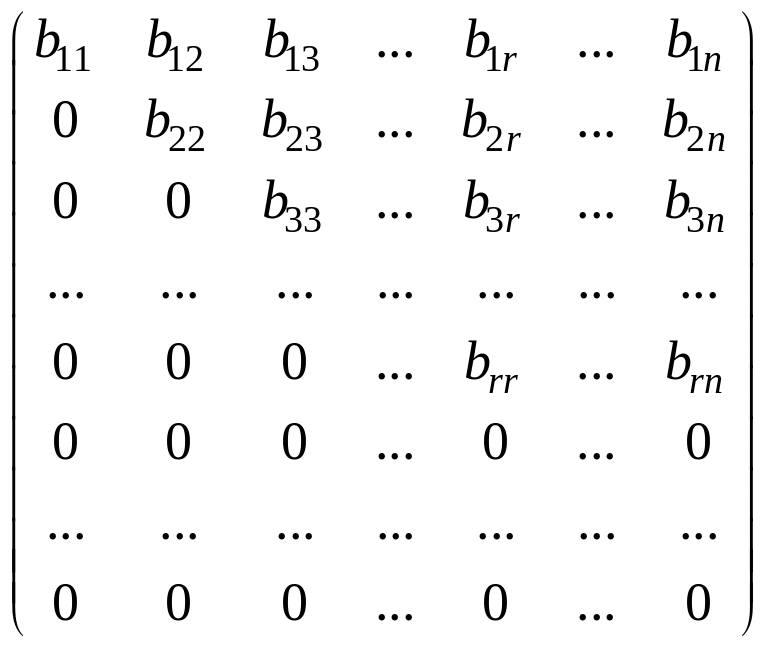где b_ii ≠0, i = 1, 2, …, r. Ранг матрицы В равен r. Действительно, вычеркнув нулевые строки, получим матрицу размерности r×n. Ранг этой матрицы равен r, так как ее минор r-го порядка, стоящий в левом верхнем углу, не равен нулю:

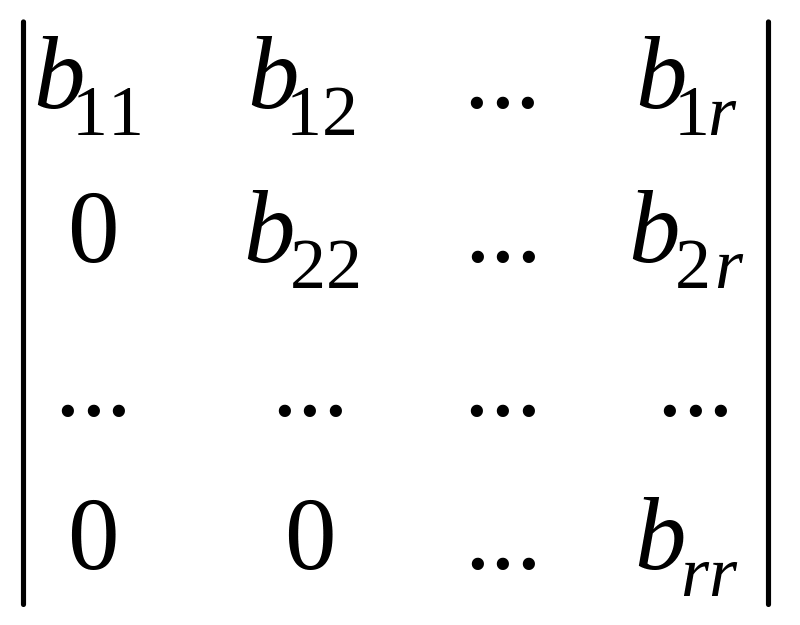= b₁₁·b₂₂·b₃₃·….b_rr ≠ 0.

Поскольку матрица В получена из матрицы А путем элементарных преобразований, то rang A = rang B.

В трапециевидной матрице ранг равен числу ее ненулевых строк.

Пример 3. Найти ранг матрицы

А = .

Решение. Производя последовательно элементарные преобразования, будем иметь:

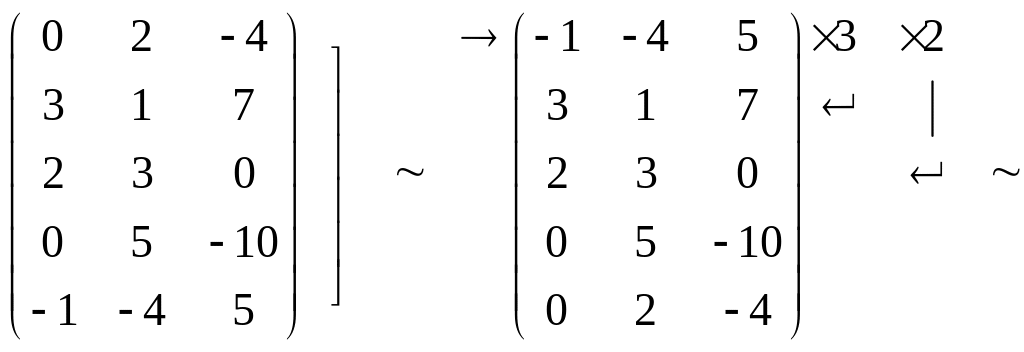
Последнюю строку мы поменяли местами с первой. Затем элементы первой строки умножили на 3 и на 2 и сложили с соответствующими элементами второй и третьей строк.

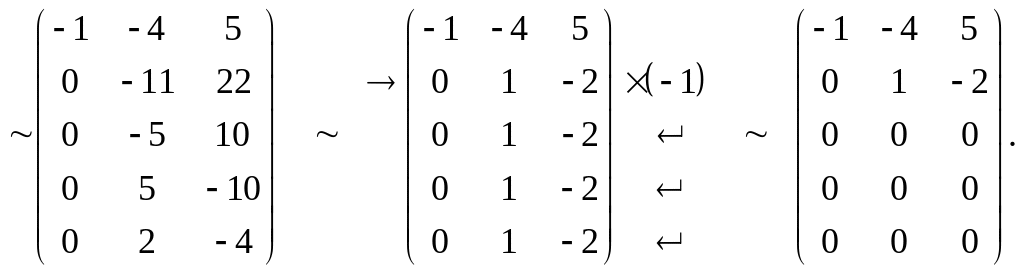
Далее элементы второй строки разделили на (–11), третьей на (–5), четвертой на 5, пятой на 2. Потом элементы второй строки умножили на (–1) и сложили с соответствующими элементами третьей, четвертой и пятой строк.

Последняя матрица трапециевидная, она имеет две ненулевых строки. Следовательно, ее ранг равен двум. Таков же ранг исходной матрицы: rang A = 2.