
Задачи, связанные с применением второго замечательного предела
Второй замечательный предел
![]() (12)
(12)
применяется
( как и в случае последовательностей)
при вычислении пределов
![]() ,
где
,
где
![]()
![]() т.е. в случае неопределённости вида
т.е. в случае неопределённости вида
Следующие три примера решим различными способами.
Пример
35.
Найти
предел
![]()
Решение.
Находим
пределы
основания и показателя степени исходного
выражения
и убеждаемся в том,
что
перед
нами
неопределённость
вида
Выделяем в исходном выражении формулу
![]() и вычисляем предел, используя (12):
и вычисляем предел, используя (12):
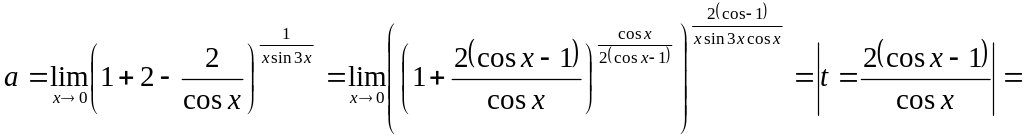


Предел выражения можно находить, предварительно вычислив предел его логарифма.
Пример
36.
Найти
предел

Решение.
Преобразуем
логарифм
исходного
выражения,
применив
формулу
![]()


 Отсюда
Отсюда
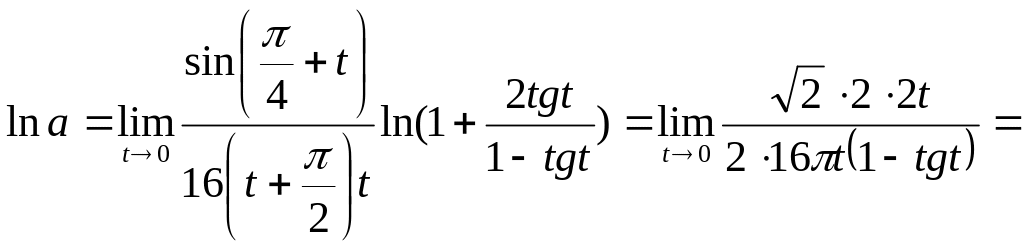
![]() Теперь
находим искомый предел:
Теперь
находим искомый предел:
![]()
Для
вычисления предела
,
где
т.е. в случае неопределённости вида
![]() ,
можно использовать правило:
,
можно использовать правило:
![]() .
(13)
.
(13)
Пример
37.
Найти
предел
![]()
Решение. Находим
![]()
Далее,
![]()
![]()
![]() и
в силу (13) получаем
и
в силу (13) получаем
![]()
Пример
38.
Последовательность
функций
![]() определяется
следующим образом:
определяется
следующим образом:
![]() Найти
Найти
![]()
Решение.
Легко
заметить и доказать по индукции, что![]() Оценим
разность между
Оценим
разность между
![]() и
числом
и
числом
![]() являющимся
корнем
уравнения
являющимся
корнем
уравнения
![]()
![]() .
Последнее
неравенство следует из того, что
.
Последнее
неравенство следует из того, что![]() и
и
![]() Применяя
полученное неравенство
Применяя
полученное неравенство
![]() к
разности
к
разности
![]() и
т.д., получим
и
т.д., получим
![]() то
есть
то
есть![]() .
Отсюда
видно, что
.
Отсюда
видно, что
![]()
Непрерывность функции
Определение.
Функция
![]() ,
заданная на множестве
,
заданная на множестве ![]() называется непрерывной в точке а
называется непрерывной в точке а![]() Е,
если
Е,
если
![]() (14)
(14)
Отсюда
следует, что в изолированной точке
множества Е функция непрерывна (см.
пример 42); если же а - предельная для
множества Е, то (14) означает, что
![]()
Пример
39.
Доказать,
что
функция
![]() непрерывна в точке а=2(найти
непрерывна в точке а=2(найти
![]() ).
).
Решение.
1-й способ. Поскольку
определена
при всех
значениях![]() R,
то
Е=
R и
(14) принимает вид:
R,
то
Е=
R и
(14) принимает вид:
![]()
Переходим к неравенству для значений функции:
![]() (15)
(15)
Пусть
выполнено
неравенство
![]() то
есть
то
есть
![]() Тогда
Тогда
![]() Если
теперь потребовать, чтобы выполнялось
неравенство
Если
теперь потребовать, чтобы выполнялось
неравенство
![]()
![]() ,
то
неравенство (15) также будет выполнено:
,
то
неравенство (15) также будет выполнено:
![]() Итак,
для выполнения последнего неравенства
потребовалось,
чтобы
Итак,
для выполнения последнего неравенства
потребовалось,
чтобы
![]() и
.
Поэтому
и
.
Поэтому
![]()
2-й
способ. Неравенство
![]() для значений функции выполнено, если
выполнено неравенство
для значений функции выполнено, если
выполнено неравенство
![]()
Последнее
неравенство, (квадратное относительно
![]() )
выполнено, если
)
выполнено, если
![]() Таким образом,
Таким образом,
![]()
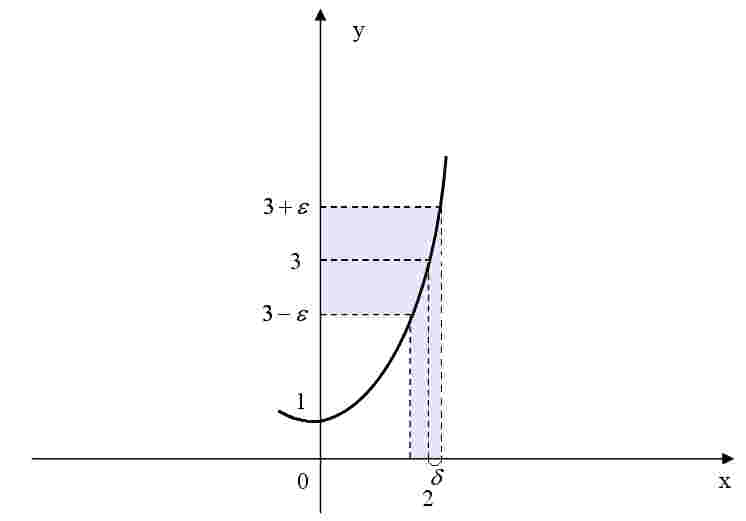
Рис.1
3-й
способ. Найдём
![]() по
по
![]() графически (см. рис. 1) и получим такой
же результат, как для второго способа
(в этом легко убедиться самостоятельно).
графически (см. рис. 1) и получим такой
же результат, как для второго способа
(в этом легко убедиться самостоятельно).
Пример
40.
С
помощью «![]() »
рассуждений доказать непрерывность
следующих функций: 1)
»
рассуждений доказать непрерывность
следующих функций: 1)
![]() :2)
:2)![]() .
.
Решение.
1).
Пусть
![]() Тогда
Тогда
![]() если
если
![]() .
Кроме того, должно выполняться условие
.
Кроме того, должно выполняться условие
![]() ,откуда
,откуда![]() и
и
![]() При а=0
При а=0
![]() если
если
![]() ( в качестве окрестности нуля в множестве
Е=D(f)
( в качестве окрестности нуля в множестве
Е=D(f)
![]() берётся
берётся
![]() ).
).
2). Покажем, что для любых х и а
![]() (16)
(16)
Из определения арктангенса и с помощью замены переменной получаем, что это неравенство равносильно неравенству
![]() где
где
![]() (17)
(17)
Если
х и а одного знака, то
![]()
Мы
воспользовались известным неравенством
![]() Из него же следует справедливость (17)
для х и а разного знака. Из неравенства
(16)следует, что в качестве искомого
можно взять
Из него же следует справедливость (17)
для х и а разного знака. Из неравенства
(16)следует, что в качестве искомого
можно взять
![]() :
если
:
если
![]() ,
то получаем, что
,
то получаем, что
![]()
