Вариант № 6

1. Производятся испытания 4–х изделий на надёжность, причём вероятность выдержать испытания для каждого равна 0,8. Случайная величина X – число изделий, не выдержавших испытания. Для случайной величины X найти: 1) ряд распределения; 2) функцию распределения; 3) M(X) и D(X).

2. Случайная величина X задается следующим рядом распределении:

	0	3	5	7
	0,2	с	0,25	0,1

Найти: 1) с, 2) ряд распределения; 3) функцию распределения; 4) M(X) и D(X);

5) .

3. Случайная величина X имеет функцию распределения

.

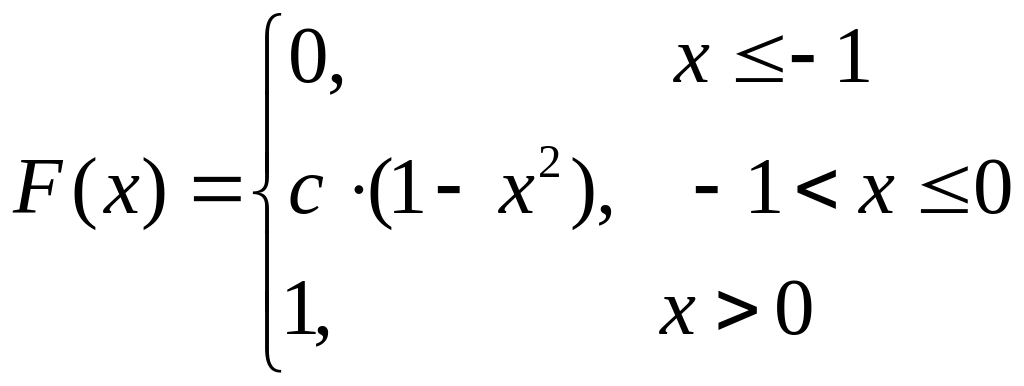Найти: 1) параметр с; 2) функцию плотности f(x); 3) P(X < – 0,5); 4) математическое ожидание M(X) и дисперсию D(X); 5) графики функций F(x) и f(x).

4. Случайная величина X равномерно распределена на [a, b]. Дано математическое ожидание M(X) = 0,5 и дисперсия D(X) = 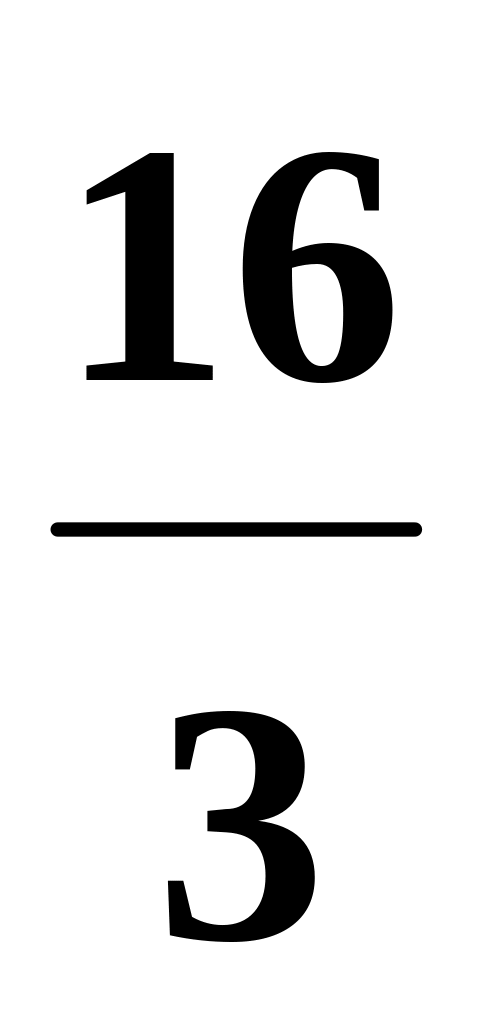. Найти: а) значения параметров a, b; б) функцию плотности f(x) и функцию распределения F(x); в) вероятность попадания случайной величины X на отрезок [– 2, 3]; г) построить графики функций f(x) и F(x); показать на них геометрический смысл P (– 2  X  3).

Типовой расчёт по теории вероятностей и случайным величинам

Вариант № 7

1. Игральную кость бросили 3 раза. Случайная величина X – число выпадений двух очков. Для случайной величины X найти: 1) ряд распределения; 2) функцию распределения; 3) M(X) и D(X).

2. Случайная величина X задается следующим рядом распределении:

	1	4	5	7
	с	0,25	0,25	0,1

Найти: 1) с, 2) ряд распределения; 3) функцию распределения; 4) M(X) и D(X);

5) .

3. Случайная величина X имеет функцию распределения

.

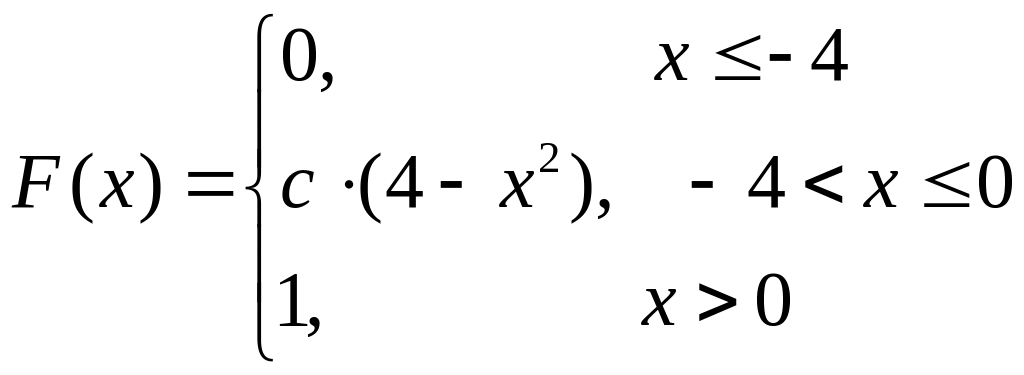Найти: 1) параметр с; 2) функцию плотности f(x); 3) P(X < – 0,5); 4) математическое ожидание M(X) и дисперсию D(X); 5) графики функций F(x) и f(x).

4. Случайная величина X равномерно распределена на [a, b]. Дано математическое ожидание M(X) = 5 и дисперсия D(X) = 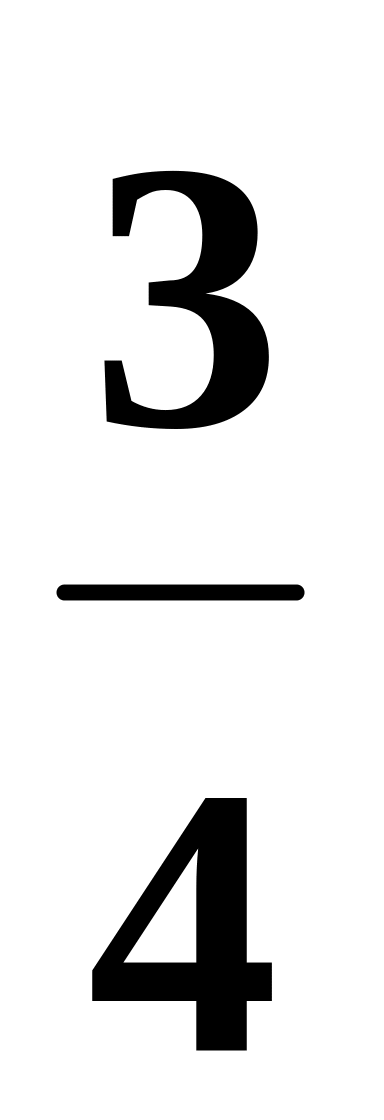. Найти: а) значения параметров a, b; б) функцию плотности f(x) и функцию распределения F(x); в) вероятность попадания случайной величины X на отрезок [0, 6]; г) построить графики функций f(x) и F(x); показать на них геометрический смысл P (0  X  6).

Типовой расчёт по теории вероятностей и случайным величинам

Вариант № 8

1. Вратарь ловит мяч при пенальти каждый раз с вероятностью 0,7. Случайная величина X – число пропущенных мячей в серии из 4–х пенальти. Для случайной величины X найти: 1) ряд распределения; 2) функцию распределения; 3) M(X) и D(X).

2. Случайная величина X задается следующим рядом распределении:

	2	4	6	8
	с	0,2	0,25	0,3

Найти: 1) с, 2) ряд распределения; 3) функцию распределения; 4) M(X) и D(X);

5) .