§ 11.6. Собственная энергия тока

Рассмотрим участок цепи, содержащий индуктивность L и сопротивление R, и приложим к его концам постоянную разность потенциалов

U = ₁ – ₂

Рис. 8.

(рис. 8). Под действием электрического поля в цепи возникает нарастающий ток I, а вместе с ним – встречная ЭДС _си . Запишем закон Ома для участка цепи 1 – 2:

IR = ₁ – ₂ – L . (10)

Домножим (10) на I и перегруппируем члены:

(₁ – ₂)I = I ²R + LI . (11)

Это выражение показывает, что мощность электрических сил частично выделяется в виде джоулева тепла, а частично идет на работу против ЭДС самоиндукции. Работа эта совершается лишь при нарастании тока, когда действует _си , причем она, очевидно, «обратима», т. е. при убывании тока сторонние силы индукции изменят направление на противоположное и совершат точно такую же работу. Ее называют собственной энергией тока U_соб .

Рис. 9.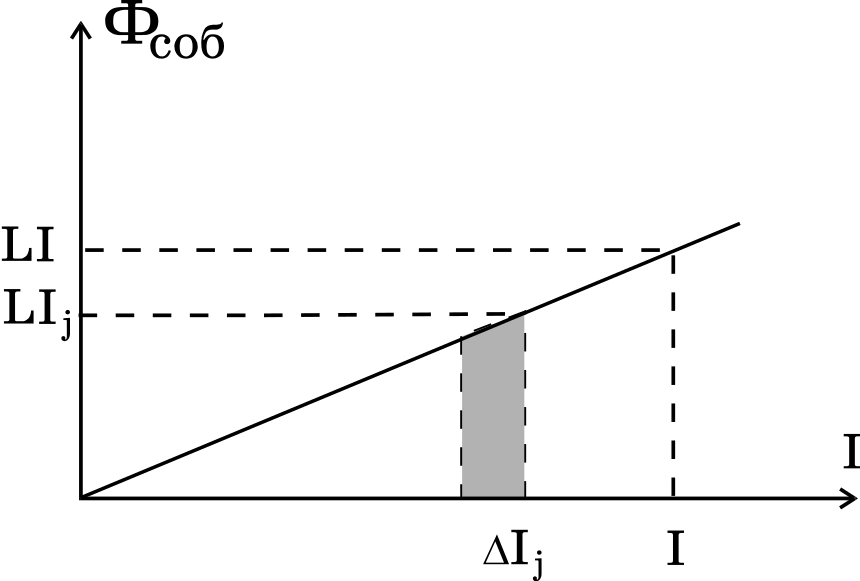

Итак, собственная энергия тока – это работа, которую нужно совершить против возникающих сил индукции, чтобы создать этот ток (она же выделится при исчезновении тока). Для нахождения U_соб построим график зависимости Ф_соб от I (рис. 9). При нарастании тока на величину I_j за время t будет, очевидно, в соответствии с (11) совершена работа против сил индукции

A_j = LI_j I_j ,

не зависящая от времени этого нарастания и численно равная площади заштрихованной на рис. 9 трапеции. При достижении тока I полная работа против сторонних сил, т. е. собственная энергия этого тока, окажется равной площади под прямой LI :

U_соб = = . (12)

По аналогии с электростатикой можно и здесь ввести понятие взаимной и полной энергии системы токов, однако, ввиду значительной их сложности, мы исключим их из рассмотрения.

§ 11.7. Энергия магнитного поля

Поскольку возникающая ЭДС самоиндукции и, следовательно, собственная энергия тока обусловлены появлением меняющегося магнитного поля, естественно попытаться связать эту энергию именно с полем. Для этого выразим собственную энергию тока в соленоиде через индукцию возбуждаемого им однородного поля. С учетом (8) и (12л17)

т. е. энергия эта оказывается пропорциональной объему V = lS, занятому полем. Ее называют энергией магнитного поля W_ , а энергию, приходящуюся на единичный объем

w_ = (13)

– плотностью энергии поля.

Можно показать, что в общем случае неоднородного поля произвольной системы токов их полная энергия, т. е. работа, которую нужно затратить против сил индукции, чтобы возбудить эти токи, представима в виде энергии магнитного поля

(14)

где суммирование распространяется на весь объем, занятый полем.

В рамках магнитостатики оба взгляда на энергию равноправны, ибо одинаково хорошо согласуются с экспериментом. Изучая же переменные электромагнитные поля, мы увидим, что там эквивалентность этих трактовок нарушается и опыту соответствует лишь представление о локализации энергии в электромагнитном поле⁵³.

Контрольные вопросы и задания

1. Получить выражение для ЭДС индукции в движущемся проводнике для случая .

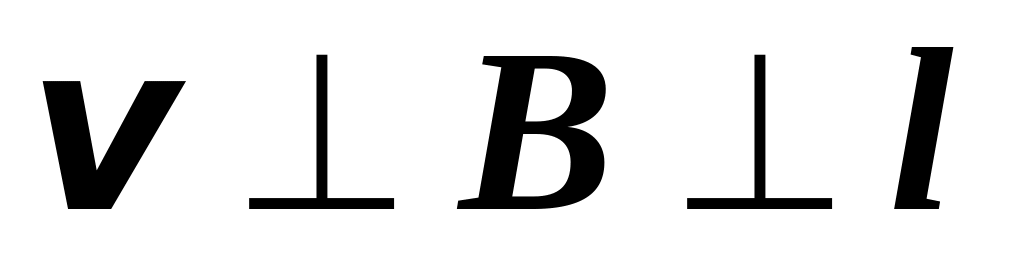2. Показать, что при появлении тока в проводнике выражение, полученное в задании 1, не меняется, а также, что работа, произведённая над ним внешней силой, равна работе индуцированной в проводнике ЭДС.

3. Привести полученное в задании 1 выражение к форме закона индукции токов в движущихся проводниках.

4. Привести соображения, позволяющие обобщить закон индукции токов в движущихся проводниках на случай неподвижного проводящего контура в меняющемся магнитном поле.

5. Сформулировать закон индукции Фарадея. Что означает в нём знак минус? Какие две физически различные ситуации он охватывает?

6. В каких случаях возникает индукционная ЭДС в проводящем контуре? В непроводящем контуре?

7. В чём причина появления индукционной ЭДС в непроводящем контуре? Как её можно обнаружить?

8. Почему вихревое индукционное поле называется электрическим, а не сторонним?

9. Дать названия и определения единиц магнитного потока и магнитной индукции.

10. Сформулировать и пояснить правило Ленца.

11. Дать определения индуктивности и единицы её измерения.

12. Найти индуктивность длинного соленоида и получить оттуда единицу измерения μ_0.

13. Получить выражение для ЭДС самоиндукции.

14. Что такое экстратоки размыкания?

15. Что называется собственной энергией тока? Чему она равна?

16. Что называется энергией магнитного поля? Получить выражение для этой энергии, рассматривая длинный соленоид.

17. Что называется плотностью энергии магнитного поля? Привести общее выражение для энергии магнитного поля.

18. Можно ли в рамках магнитостатики экспериментально установить, с чем именно связана магнитная энергия: с магнитным полем или с возбуждающими его токами? Если да, то как именно, если нет – почему?