
- •Часть III
- •Раздел 2 Издательство сунц мгу
- •Лекция 14
- •Глава 9. Постоянный электрический ток § 9.1. Электрическое поле постоянного тока
- •§ 9.2. Законы Ома и Джоуля
- •§ 9.3 Сопротивление однородного цилиндрического проводника
- •§ 9.4. Сопротивление проводника произвольной формы
- •§ 9.5. Закон Ома в дифференциальной форме
- •§ 9.6. Условие стационарности токов
- •Контрольные вопросы и задания
- •Лекция 15 § 9.7.Сторонние электродвижущие силы (эдс)
- •§ 9.8. Закон Ома для участка цепи со сторонней эдс
- •§ 9.9. Закон Ома для замкнутой цепи. Правила Кирхгофа
- •§ 9.10. Обобщенный закон Джоуля. Превращения энергии в цепи постоянного тока
- •Контрольные вопросы и задания
- •Лекция 16
- •Глава 10. Магнитостатика
- •§ 10.1. Взаимодействие постоянных токов
- •§ 10.2. Векторное произведение векторов
- •§ 10.3. Вектор магнитной индукции
- •§ 10.4. Закон Био – Савара. Принцип суперпозиции
- •§ 10.5. Взаимодействие элементов тока
- •Контрольные вопросы и задания
- •Лекция 17
- •§ 10.6. Теорема о циркуляции
- •§ 10.7. Полная система уравнений магнитостатики. Теорема единственности
- •§ 10.8. Сила Лоренца
- •Контрольные вопросы и задания
- •Лекция 18
- •Глава 11. Электромагнитная индукция
- •§ 11.1. Эдс индукции в движущихся проводниках
- •§ 11.3. Исключения из «правила потока»
- •§ 11.4. Правило Ленца
- •§ 11.5. Самоиндукция
- •§ 11.6. Собственная энергия тока
- •§ 11.7. Энергия магнитного поля
- •Контрольные вопросы и задания
- •Оглавление
- •Глава 9. Постоянный электрический ток 3
- •§ 9.1. Электрическое поле постоянного тока 3
§ 10.4. Закон Био – Савара. Принцип суперпозиции
Определение магнитного поля (5), по существу, наполняется физическим содержанием лишь после того, как будет описано, каким образом оно возбуждается текущими токами. Ведь экспериментально проверяется именно действие тока на ток, и без этого описания определение (5) «повисает в воздухе».
Следуя аналогии с электростатикой, мы должны теперь сформулировать закон (аналогичный закону Кулона для поля), позволяющий рассчитать магнитное поле, создаваемое в любой точке пространства (в вакууме) данным элементом линейного тока. Однако, оставаясь в рамках магнитостатики, этого сделать нельзя, ибо, как уже отмечалось, любая цепь постоянного тока замкнута и отдельного элемента такого тока не существует. Таким образом, мы всегда имеем дело с результирующим полем всех элементов этой цепи, а знания результирующей недостаточно для однозначного определения составляющих.
Тем не менее, выходя за эти рамки, т. е. оперируя с переменными токами, могущими быть незамкнутыми и, таким образом, составлять отдельный элемент тока, все-таки удается сформулировать (и экспериментально подтвердить) интересующий нас закон. Он носит название закона Био – Савара20 и выглядит (в системе СИ) следующим образом:
![]() , (8)
, (8)
где R – радиус-вектор, проведенный из (любой) точки элемента тока Il в точку наблюдения, где этим током создается поле B, а 0 = 4 10–7 ед. СИ – размерный коэффициент, называемый магнитной постоянной21.
Из этого закона следует, что поле элемента по величине
![]() (9)
(9)
Рис. 4.
Рис. 5.
Рис. 6.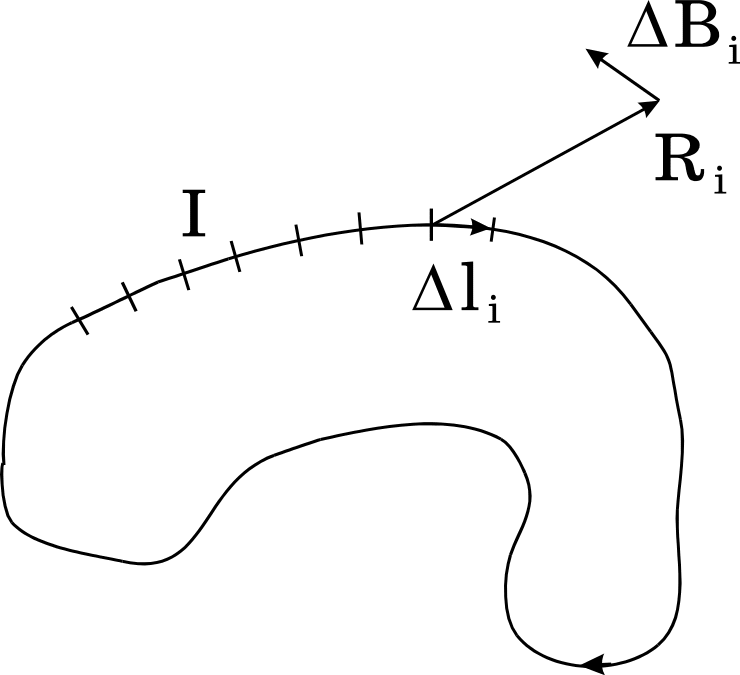
![]() , (10)
, (10)
где суммирование производится по всем участкам, на которые разбит линейный ток I.
Пример.
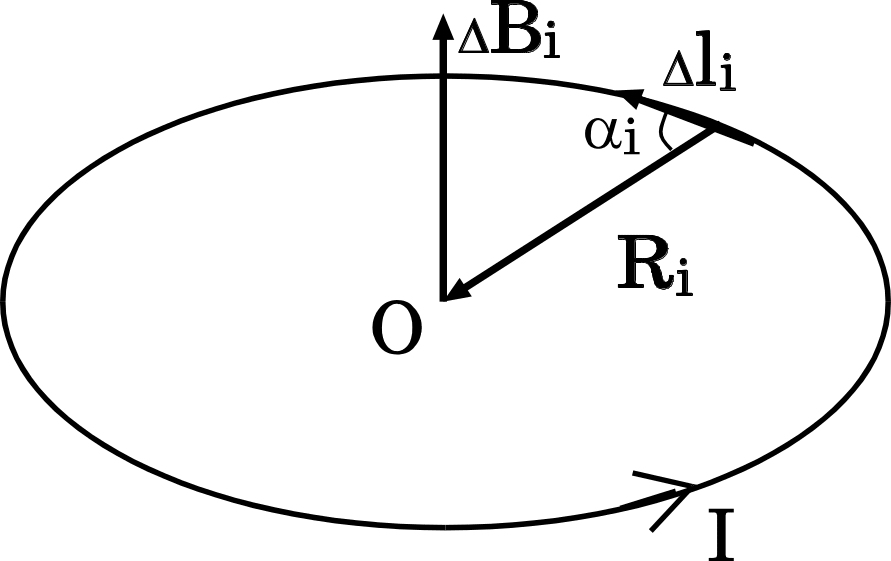
Найти индукцию магнитного поля в центре
кольца радиуса R, несущего линейный
ток I (рис. 6).
Разобьем кольцо на маленькие отрезки
li
и посчитаем вклад
![]() каждого из них в искомое поле.
Очевидно, все
будут перпендикулярны плоскости кольца
и направлены на рис. 6 вверх. Абсолютная
величина
в соответствии с (9)
каждого из них в искомое поле.
Очевидно, все
будут перпендикулярны плоскости кольца
и направлены на рис. 6 вверх. Абсолютная
величина
в соответствии с (9)
![]() =
=![]() ,
,
ибо все
![]() = / 2
и все
= / 2
и все
![]() = R.
Суммируя вклады всех участков кольца,
получим
= R.
Суммируя вклады всех участков кольца,
получим
B =![]() =
=![]() =
=![]() .
.
Отметим, что по направлению вектор B образует с направлением тока в кольце правовинтовую систему.
