1 Кинематический анализ механизма

1.1 Структурный анализ

1.1.1.Вычерчиваем структурную схему механизма поперечно-строгального станка

Рисунок 2-Схема механизма поперечно строгального станка

Определим степень подвижности механизма по формуле Чебышева:

W=3n-2P -P , (1.1)

где n – число подвижных звеньев;

P - число кинематических пар пятого класса;

P - число кинематических пар четвертого класса.

n=5(1,2,3,4,5); P =7 ; P =0.

Подставив эти данные в формулу (1.1), получим:

W=3 5-2 7-0=1.

При W=1 в схеме механизма одно ведущее звено. Это звено O₁A.

Определяем класс механизма. Для этого разобьем механизм на группы Ассура и его класс определим по классификации Ассура-Артоболевского (см.таблицу 1).

Запишем формулу строения механизма:

I(1,6)2³(2,3) 2²(4,5).

Следовательно, механизм поперечно – строгального станка – механизм второго класса, так как наивысший класс присоединенных групп Ассура – второй.

1.1.2 Построение планов положений исследуемого механизма

Выбираем масштаб длин:

= , (1.2)

₌ =0,003 ,

где - истинная длина кривошипа;

O₁A– выбранный чертежный размер.

Рассчитаем чертежные размеры звеньев и сведем их в таблицу 1.1.

Таблица 1.1 - Чертежные размеры звеньев

O1A	O1O2	O2B	BC	X1	X2	Y
40	150	276	97	183	141	123

1.2 Построение планов скоростей и ускорений механизма

Построение начинаем от ведущего звена O₁A в следующей последовательности:

1. Находим скорость точки A:

= , (1.3)

=7,2 0,12=0,864 м/сек

где - угловая скорость кривошипа, которую определяем, используя исходные данные задания.

; (1.4)

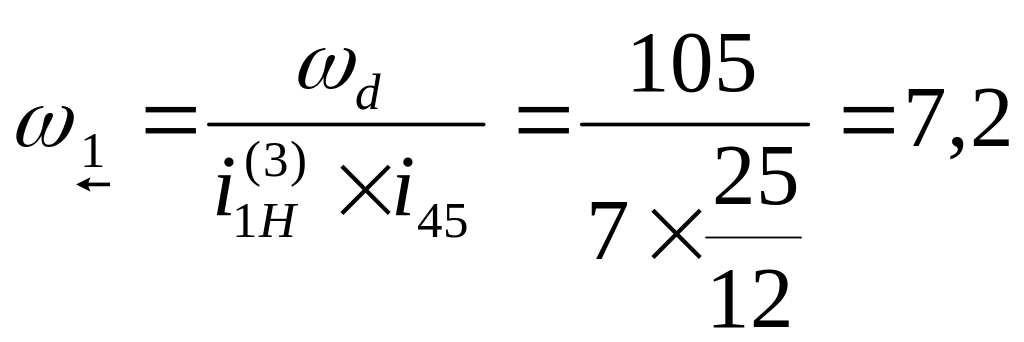. (1.5)

Значение угловой скорости кривошипа будет равно =const, тогда определяем по формуле (1.3)

2. Из полюса плана скоростей Р откладываем отрезок Рa произвольной длины, изображающий вектор скорости a.

3. Определим масштаб плана скоростей:

= = = =0,0144 .

4. Для группы Ассура второго класса третьего вида (звенья 2-3) запишем два векторных уравнения для точки A₃:

= + (1.6)

в	?		?
н	?	 O1A в стор.1	AO2

= + (1.7)

в	?	0	?
н	?	0	 AO2

5. Для группы Ассура второго класса второго вида (звенья 4-5) запишем два векторных уравнения для точки С:

= + (1.8)

в	?	из подобия	?
н	?	из подобия	BC

= + (1.9)

в	?	0	?
н	?	0	XX

Уравнения (1.6) и (1.7) решаем графически, т.е. строим план скоростей в выбранном масштабе . Пересечение линий действия скоростей и дает на плане точку a₃.

6. Скорость точки b, которая принадлежит третьему звену, определим, используя теорему подобия:

o₂b = (1.10)

Данные для каждого положения механизма сводим в таблицу 1.2.

Таблица 1.2 – Значение длины отрезка o₂b

Положение механизма	0	1	2	3	4	5	6	7	8	9	10	11
O2B, мм	276	276	276	276	276	276	276	276	276	276	276	276
O2A3, мм	153	167	176	180	176	167	153	137	125	120	125	137
o2a3, мм	12	38	54	60	56	38	12	20	48	60	48	20
o2b, мм	19	55	74	81	77	55	19	35	93	121	93	35

От полюса P необходимо отложить о₂b, который лежит на продолжении o₂a. Полученный отрезок Pb и будет графическим изображением скорости V_B на плане скоростей. Далее, из точки b проводится линия действия скорости V_CB, а из полюса Р линия действия скорости V_CC6 . Пересечение линий действия этих скоростей дает на плане точку c. Отрезок Рc будет графическим изображением скорости V_C. Так графически решаются уравнения (1.8) и (1.9).

7. Далее посередине отрезка Pb и cb отмечаем точки s3, s4 соответственно и соединяем их с полюсом p. Получаются вектора графически изображающие скорости точек s3 , s4 на плане скоростей.

Длины отрезков на плане скоростей сводим в таблицу 1.3.

Таблица 1.3 – Длины векторов плана скоростей

Положение механизма		0	1	2	3	4	5		6	7		8	9		10	11
Pa		60	60	60	60	60	60		60	60		60	60		60	60
a3a		59	47	25	0	25	47		59	57		36	0		36	57
Pa3		12	38	54	60	56	38		12	20		48	60		48	20
Pb		19	55	74	81	77	55		19	35		93	121		93	35
Pc		17	56	84	96	88	63		21	34		96	121		88	29
cb		4	10	8	0	8	10		4	6		12	0		12	6
		18	58	85	0	87	62		20	33		94	0		90	30
	9		30	43	48	43	30	10		15	46		60	46		16