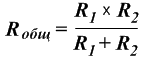20. Гармонический ток через цепь последовательно соединенных элементов r, l и с. Комплексное сопротивление. Реактивное сопротивление. Векторные диаграммы напряжений и тока.

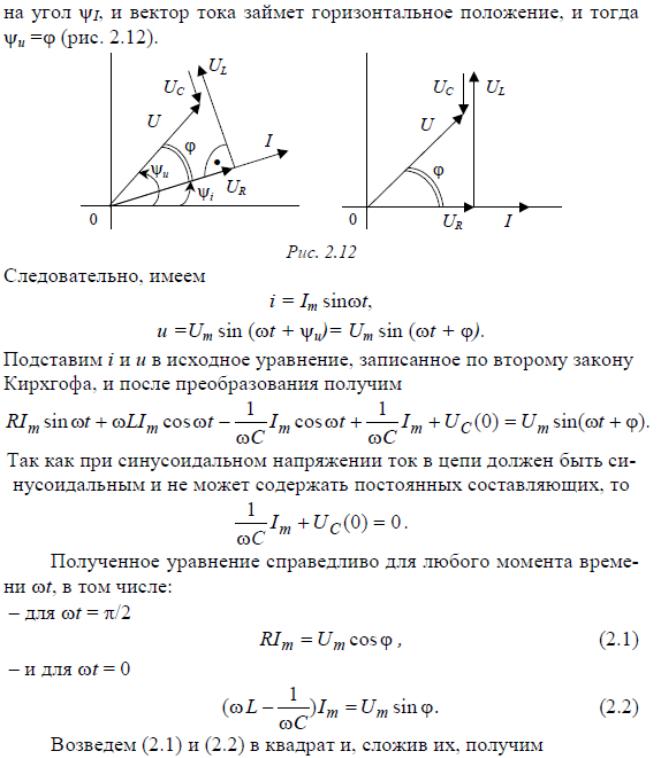
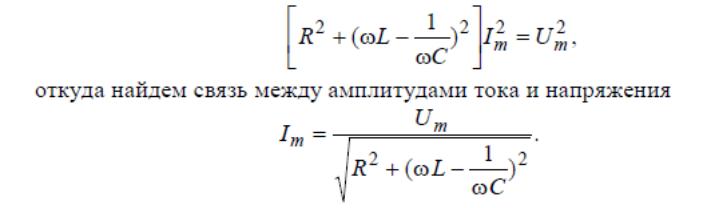
21. Гармонический ток через цепь последовательно соединенных элементов r, l и с. Комплексное сопротивление. Треугольник сопротивлений.

Угол сдвига фаз в этом выражении можно найти построив векторную диаграмму, однако проще всего это можно сделать применив комплексный метод.

Реактивные сопротивления элементов цепи: X_C = 1/ωC; X_L = ωL

Комплексное сопротивление цепи запишется в форме:

Z = R + j(X_­L – X_C) = R + j(ωL – 1/ωC) .

Модуль комплексного сопротивления называется полным электрическим сопротивлением

Сдвиг фаз в цепи найдем по соотношению:

22. Гармонический ток в цепи параллельно соединенных элементов r, l и с. Комплексная проводимость. Реактивная проводимость. Векторные диаграммы напряжения и токов.

23. Гармонический ток в цепи параллельно соединенных элементов r, l и с. Комплексная проводимость. Треугольник проводимостей.

Реактивные сопротивления элементов цепи: X_C = 1/ωC; X_L = ωL

Реактивная проводимость – величина обратная реактивному сопротивлению.

Комплексная проводимость цепи запишется в форме:

Y = G + j(X_­L – X_C) =G + j(ωC – 1/ωL) .

Векторная диаграмма цепи имеет вид:

Из векторной диаграммы получаем треугольник проводимостей.

Здесь показанные значения вычисляются по формулам

24. Расчет мощности. Активная (средняя), реактивная и полная комплексная мощность. Треугольник мощностей. Коэффициент мощности.

Множитель cosφ называют коэффициентом мощности.

25. Баланс мощностей в цепях гармонического тока. Топографическая диаграмма.

Баланс мощностей является следствием закона сохранения энергии и может служить критерием правильности расчета электрической цепи.

Из закона сохранения энергии следует, что сумма всех отдаваемых активных мощностей равна сумме всех потребляемых активных мощностей, т.е.

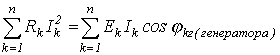
Баланс соблюдается и для реактивных мощностей:

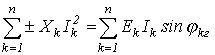
где знак "+” относится к индуктивным элементам , "-” – к емкостным.

Умножив последнее выражение на j и сложив полученный результат с предпоследним, придем к аналитическому выражению баланса мощностей в цепях синусоидального тока (без учета взаимной индуктивности):

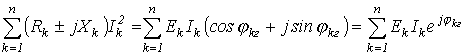
или

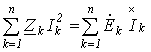
Топографическая диаграмма представляет собой диаграмму комплексных потенциалов точек цепей нанесённую на комплексную плоскость.

Потенциал одной из точек цепи принимается равным 0 и рассчитываются комплексы потенциалов всех остальных точек.

Полученные комплексы потенциалов наносятся на комплексную плоскость и полученные точки соединяются отрезками прямых в соответствии со схемой.

Пример топографической диаграммы для простейшей цепи:

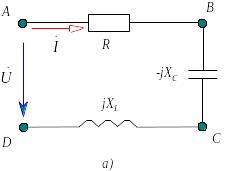
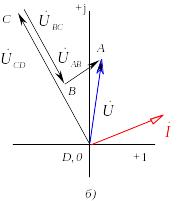
26. Делители напряжения и тока.

Простейший резистивный делитель напряжения представляет собой два последовательно включённых резистора R₁ и R₂, подключённых к источнику напряжения U.

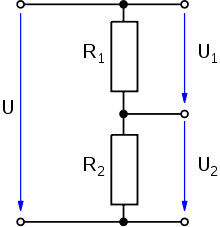
Поскольку резисторы соединены последовательно, то ток через них будет постоянен. Падение напряжения (уменьшение потенциала при перемещении заряда от одной точки цепи до другой её точки) на каждом резисторе согласно закону Ома будет пропорционально сопротивлению (ток, как было установлено ранее, постоянен):

.

Для каждого резистора:

Разделив выражение для U₁ на выражение для U₂ в итоге получаем:

Таким образом, отношение напряжений U₁ и U₂ в точности равно отношению сопротивлений R₁ и R₂.

Делитель тока на резисторах предназначен для того, чтобы, не изменяя общего тока протекающего через электрическую цепь, часть его направить в другое плечо делителя. Делитель тока применяется в измерительных приборах, когда необходимо измерить большой ток (единицы, или сотни Ампер) прибором, рассчитанным на маленький ток (миллиамперы или даже микроамперы). В этом случае, внутреннее сопротивление измерительного прибора выступает в качестве одного из резисторов, а второй резистор в таком случае называют «шунтом», так как он шунтирует проходящий ток (берёт часть нагрузки «на себя»).

Изобразим цепь делителя тока:

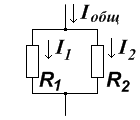
На рисунке видно, что общий входящий ток делится на два, и проходя цепь, снова объединяется в один.

Расчёт делителя тока на резисторах основывается на законе Ома, правиле сложения токов (законе Киргофа) и формуле параллельного соединения резисторов:

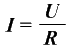(1)