12. Мгновенная и средняя мощности гармонических колебаний.
Мгновенная мощность гармонических колебаний равна: Рm = i∙u, где u и i - мгновенные значения напряжения и тока. Величины тока и напряжения, входящие в выражение, являются синусоидальными функциями времени, поэтому и мгновенная мощность является переменной величиной. График этой величины представлен на рисунке.
Для оценки используется понятие средней мощности за период. Ее можно получить, интегрируя за период T работу, совершаемую электрическим полем, а затем соотнося ее с величиной периода, т.е.
Пусть u=Umsinwt и Imsin(wt − φ), тогда средняя мощность будет равна
т.к. интеграл второго слагаемого равен нулю. Величина cosφ называется коэффициентом мощности.
Из этого выражения следует, что средняя мощность в цепи переменного тока зависит не только от действующих значений тока I и напряжения U, но и от разности фаз φ между ними. Максимальная мощность соответствует нулевому сдвигу фаз и равна произведению UI. При сдвиге фаз между током и напряжением в φ = 90° средняя мощность равна нулю.
P = UI cosφ = U(I cosφ ) = UIа = I(U cosφ ) = IUа .
Учитывая, что активные составляющие тока и напряжения можно выразить через резистивную состаляющую комплексного сопротивления цепи как Iа=U/R или Uа=IR , выражение (4) можно записать также в форме P = I2R = U2/R .
Среднюю мощность P называют также активной мощностью и измеряют в ваттах [Вт].
Выделим подинтегральную функцию выражения (3)
Отсюда следует, что мгновенная мощность изменяется с двойной частотой сети относительно постоянной составляющей UIcosφ равной средней или активной мощности.
13. Гармонический ток через резистор, напряжение на резисторе. Мгновенная и средняя мощность. Временная и векторная диаграммы тока, напряжения и мощности.
Активное электрическое сопротивление – параметр пассивного двухполюсника, равный отношению активной мощности, поглощаемой в этом двухполюснике, к квадрату действующего значения тока через этот двухполюсник (ГОСТ Р52002-2003).
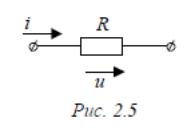
Пусть к активному сопротивлению (рис.2.5) приложено синусоидальное напряжение
u=Um sin(wt+ φU ) с начальной фазой φU = 0. Тогда по закону Ома
u = iR, iR=Umsinwt,
-
i =
Um sinwt
, φi = 0
R
Значит φ = φi – φU = 0
, .
На участке цепи с активным сопротивлением ток совпадает по фазе с напряжением на этом участке.
Мгновенная мощность:
-
Рm = i∙U =
U2m sin2wt
R
Средняя мощность:
-
Рср =
U2m
2R
Векторная диаграмма действующих значений тока и напряжения, графики зависимостей мгновенных значений тока и напряжений приведены на рис. 2.6.
Рис. 2.6