9. Метод наложения, план анализа, пример.

Метод применяется для расчета цепей, содержащих несколько (два и более) источников электрической энергии. Подчеркнем, что этот метод применим для расчета только линейных цепей. Метод основывается на том положении, что в каждой ветви цепи ток равен алгебраической сумме токов, создаваемых каждым источником. Следовательно, необходимо определить токи, создаваемые каждым источником в отдельности, а затем их просуммировать с учетом направлений.

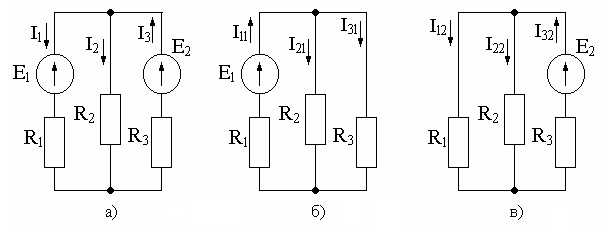
Рис.1.18. Пример расчета методом наложения

Последовательность расчета:

1. В электрической цепи оставляют только один источник ЭДС. Вместо исключенного источника ЭДС ставится или резистор, величина которого равна величине внутреннего сопротивления источника ЭДС, или перемычка, если внутреннее сопротивление источника равно нулю.

2. Определяются токи во всех ветвях, создаваемые этим источником ЭДС.

3. Оставляется в цепи следующий источник ЭДС, а с остальными поступают аналогично тому, как сказано в п. 1.

4. Определяются токи в цепи, создаваемые вторым источником ЭДС.

5. Аналогично поступают с оставшимися источниками.

6. Истинные токи в ветвях цепи определяются как алгебраическая сумма токов в этих ветвях, созданных каждым из источников.

Рассчитаем цепь, изображенную на рис. 1.18, методом наложения. Будем считать, что внутренние сопротивления источников ЭДС равны нулю.

В начале оставляем источник E₁, а источник E₂ убирается и в место него ставится перемычка (рис. 1.18, б). В полученной схеме находим токи методом эквивалентного преобразования:

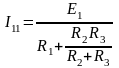
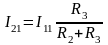
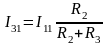
Затем оставляем только источник E₂, а вместо E₁ ставится перемычка (рис. 1.18, в). В полученной схеме определяем токи в ветвях также методом эквивалентного преобразования:

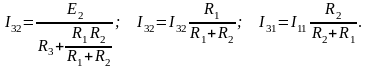
Находим действительные токи в исходной схеме (рис. 1.18, а) алгебраическим суммированием найденных токов.

Ток I₁ равен разности тока I₁₁ и тока I₁₂:

I₁ = I₁₁ – I₁₂.

Ток I₂ равен сумме токов I₂₁ и I₂₂, т. к. они совпадают по направлению:

I₂ = I₂₁ + I₂₂.

Ток I₃ равен разности тока I₃₂ и тока I₃₁:

I₃ = I₃₂ – I₃₁.

10. Теорема об эквивалентном источнике напряжения. Метод эквивалентного генератора, план анализа, пример.

Теореме об эквивалентном источнике напряжения:

" Ток в любой ветви линейной электрической цепи не изменится, если электрическую цепь, к которой подключена данная ветвь, заменить эквивалентным источником напряжения. ЭДС этого источника должна быть равна напряжению на зажимах разомкнутой ветви, а внутреннее сопротивление источника должно равняться входному сопротивлению пассивной электрической цепи со стороны зажимов подключения ветви при разомкнутой ветви".

Последовательность расчета:

1. Отсоединить от схемы интересующую ветвь, клеммы подсоединения которой обозначить через а–б.

2. Рассчитать оставшуюся часть цепи и определить напряжение на клеммах а–б (U_аб).

3. В оставшейся части цепи заменить источники ЭДС перемычкой или резистором, сопротивление которого равно резистором с сопротивлением R₀. Эту цепь подсоединить к клеммам а–б.

6. К клеммам а–б подсоединить интересующую ветвь и определить ток, протекающий через нее.

Определим ток в ветви а–б схемы (рис. 1.20, а) методом эквивалентного источника напряжения.

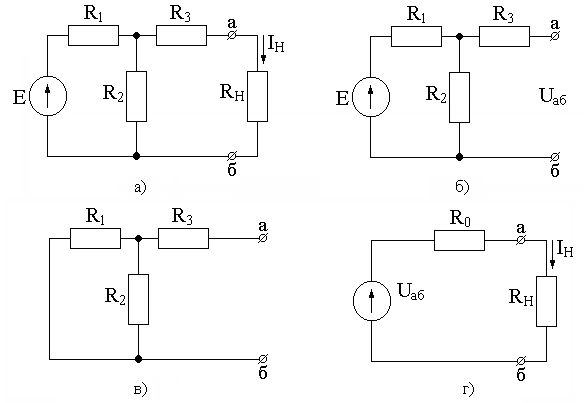
Рис. 1.20. Пример расчета методом эквивалентного источника напряжения

Отключаем ветвь а–б (рис. 1.20, б) и находим напряжение на клеммах а–б:

.

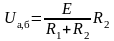Далее исключаем у оставшейся схемы источник E, заменяя его перемычкой, считая, что его внутреннее сопротивление равно нулю (рис. 1.20, в) и определяем сопротивление цепи относительно клемм а–б:

.

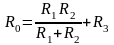Теперь составляем схему (рис. 1.20, г) и находим ток в ветви а–б:

.

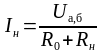11. Способы представления гармонических колебаний. Параметры гармонического колебания, амплитуда, фаза, частота, угловая частота, начальная фаза. Среднее, среднее на периоде, действующее значение гармонических колебаний.

В настоящее время переменный ток находит широкое применение в технике, так как он легко трансформируется и передается на большие расстояния при высоком напряжении и малых потерях. В электротехнике наибольшее распространение получил синусоидальный переменный ток, то есть ток, величина которого изменяется по закону синуса. Поэтому мгновенное значение синусоидального тока выражается формулой

где - амплитуда тока, Т - период – время, за которое совершается одно полное колебание, с; f = 1/T - частота, равная числу колебаний за 1 секунду (единица измерения частоты – Герц (Гц) или с^-1 ); ω – угловая частота (выражается в рад/с или с^-1 ).

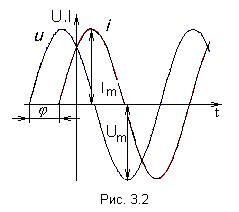Аргумент синуса, то есть называют фазой. Фаза характеризует состояние колебания (его численное значение) в данный момент времени t. Любая синусоидально изменяющаяся функция определяется тремя величинами: амплитудой, угловой частотой и начальной фазой. Если частота слишком низкая, то увеличиваются габариты электрических машин и, следовательно, расход материалов на их изготовление. При слишком больших частотах увеличиваются потери энергии в сердечниках электрических машин и трансформаторах.

Среднее и действующее значения синусоидально тока синусоидально изменяющейся величины понимают её среднее значение за полпериода.

То есть среднее значение синусоидального тока составляет от амплитудного значения.

Переменный ток обычно характеризуется его действующим значением .

Значит, действующее значение синусоидального тока равно 0,707 от амплитудного