
- •1. Закон Ома для участка цепи.
- •3. Способы соединения идеализированных элементов и эквивалентные преобразования. Последовательное соединение, параллельное соединение, смешанное соединение.
- •Смешанное соединение – комбинация параллельного и последовательного соединений.
- •4. Преобразование треугольника в эквивалентную звезду, Преобразование звезды в эквивалентный треугольник. Эквивалентные источники напряжения и тока. Понятие о дуальности электрических цепей.
- •5. Законы Кирхгофа для мгновенных величин. Распределение потенциала вдоль цепи с сопротивлениями и источниками напряжения. Потенциальная диаграмма. Баланс мощностей.
- •6. Метод расчета сложных схем с использованием уравнений Кирхгофа, план анализа, пример.
- •7. Метод контурных токов, план анализа, пример.
- •8. Метод узловых потенциалов, план анализа, пример.
- •9. Метод наложения, план анализа, пример.
- •10. Теорема об эквивалентном источнике напряжения. Метод эквивалентного генератора, план анализа, пример.
- •12. Мгновенная и средняя мощности гармонических колебаний.
- •13. Гармонический ток через резистор, напряжение на резисторе. Мгновенная и средняя мощность. Временная и векторная диаграммы тока, напряжения и мощности.
- •14. Гармонический ток через индуктивность, напряжение на индуктивности. Мгновенная и средняя мощность. Временная и векторная диаграммы тока, напряжения и мощности.
- •1 5. Гармонический ток через конденсатор, напряжение на конденсаторе. Мгновенная и средняя мощность. Временная и векторная диаграммы тока, напряжения и мощности.
- •16. Гармонический ток через цепь последовательно соединенных элементов r и l. Векторная диаграмма тока и напряжения.
- •17. Гармонический ток через цепь последовательно соединенных элементов r и с. Векторная диаграмма тока и напряжения.
- •18. Метод комплексных амплитуд. Комплексные амплитуды и комплексные действующие значения. Операции с комплексными значениями.
- •19. Законы Ома и Кирхгофа для комплексных действующих значений.
- •20. Гармонический ток через цепь последовательно соединенных элементов r, l и с. Комплексное сопротивление. Реактивное сопротивление. Векторные диаграммы напряжений и тока.
- •21. Гармонический ток через цепь последовательно соединенных элементов r, l и с. Комплексное сопротивление. Треугольник сопротивлений.
- •22. Гармонический ток в цепи параллельно соединенных элементов r, l и с. Комплексная проводимость. Реактивная проводимость. Векторные диаграммы напряжения и токов.
- •23. Гармонический ток в цепи параллельно соединенных элементов r, l и с. Комплексная проводимость. Треугольник проводимостей.
- •24. Расчет мощности. Активная (средняя), реактивная и полная комплексная мощность. Треугольник мощностей. Коэффициент мощности.
- •25. Баланс мощностей в цепях гармонического тока. Топографическая диаграмма.
- •26. Делители напряжения и тока.
- •27. Согласование источника энергии с нагрузкой.
- •28. Понятие о комплексных частотных характеристиках (кчх). Передаточные и входные комплексные частотные характеристики. Амплитудно-частотные и фазо-частотные характеристики.
- •29. Кчх идеализированных двухполюсных пассивных элементов (сопротивления, индуктивности, емкости).
- •30. Кчх цепей с одним реактивным элементом.
- •32. Резонансный режим работы цепи. Резонанс токов. Нахождение резонансной частоты контура. Частотные характеристики резонансного контура. Векторная диаграмма.
- •33. Разновидности параллельного колебательного контура. Нахождение резонансной частоты.
- •34. Понятие о взаимной индуктивности. Магнитный поток самоиндукции. Магнитный поток рассеяния. Магнитный поток взаимной индукции.
- •36. Трансформатор.
- •37. Генерирование гармонической эдс.
- •38. Трехфазная цепь. Способы представления токов напряжений в фазах трехфазной цепи.
- •45. Расчет мощностей. Активная, реактивная и полная мощность трехфазной цепи. Симметричная и несимметричная нагрузка.
38. Трехфазная цепь. Способы представления токов напряжений в фазах трехфазной цепи.
 39.
Способы соединения фаз генератора.
Соединения фаз генератора звездой и
треугольником. Линейные и фазные
напряжения и токи, определение. Чередование
фаз. Симметричная и несимметричная
нагрузка. Однородная и неоднородная
нагрузка.
39.
Способы соединения фаз генератора.
Соединения фаз генератора звездой и
треугольником. Линейные и фазные
напряжения и токи, определение. Чередование
фаз. Симметричная и несимметричная
нагрузка. Однородная и неоднородная
нагрузка.
Чаще всего фазы генератора соединяют звездой.
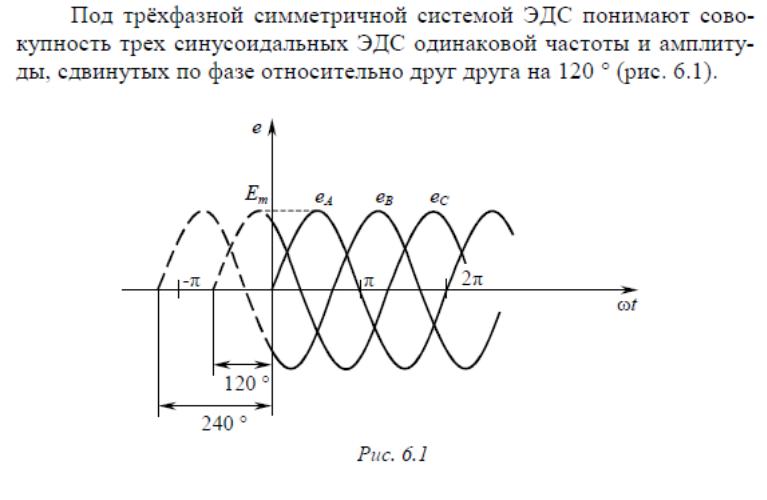
За условное положительное направление ЭДС в каждой фазе принимают направление от конца к началу. Обычно индуктированные в обмотках статора ЭДС имеют одинаковые амплитуды и сдвинуты по фазе относительно друг друга на один и тот же угол 120°. Такая система ЭДС называется симметричной.

Трехфазная симметричная система ЭДС может изображаться графиками, тригонометрическими функциями, векторами и функциями комплексного переменного.
Графики мгновенных значений трехфазной симметричной системы ЭДС показаны на рис. 3.3.
Если ЭДС одной фазы (например, фазы A) принять за исходную и считать её начальную фазу равной нулю, то выражения мгновенных значений ЭДС можно записать в виде
eA = Emsinωt, eB = Emsin(ωt−120°), eC = Emsin(ωt−240°) = Emsin(ωt+120°).

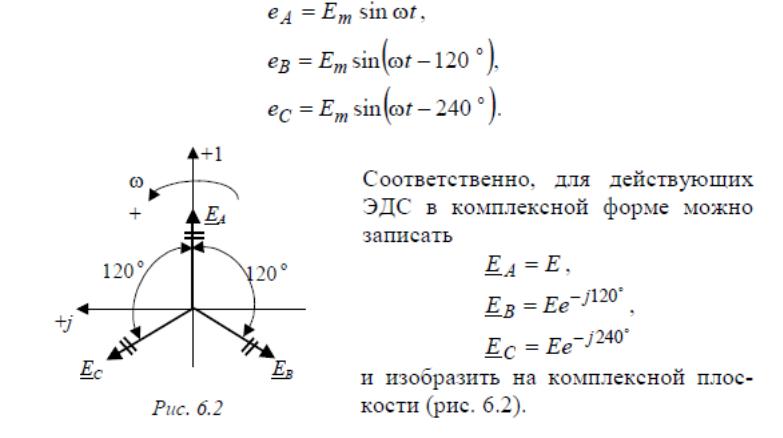
Комплексные действующие ЭДС будут иметь выражения:
ĖA = Emej0° = Em(1+j0), ĖB = Eme−j120° = Em(−1/2 − j√3/2), ĖC = Eme+j120° = Em(−1/2+j√3/2).
Эти напряжения называют фазными напряжениями.
Векторная диаграмма трехфазной симметричной системы ЭДС показана на рис 3.4а.

Рис. 3.4
На диаграмме рис. 3.4а вектор ĖA направлен вертикально, так как при расчете трехфазных цепей принято направлять вертикально вверх ось действительных величин. Из векторных диаграмм рис 3.4 следует, что для симметричной трехфазной системы геометрическая сумма векторов ЭДС всех фаз равна нулю:
ĖA + ĖB + ĖC = 0.
Систему ЭДС, в которой ЭДС фазы B отстает по фазе от ЭДС фазы A, а ЭДС фазы C по фазе – от ЭДС фазы B, называют системой прямой последовательности. Если изменить направление вращения ротора генератора, то последовательность фаз изменится (рис. 3.4б) и будет называться обратной.
Напряжение между фазами: UAB = ĖA − ĖB = Em − Em(−1/2 − j√3/2) = Em(3/2 + j√3/2) = √3Eme+j60°
Эти напряжения называют линейными напряжениями. Если сравнить их с фазными напряжениями то можно видеть, что Uл = √3Uф
При соединении источника питания треугольником (рис. 3.12) конец X одной фазы соединяется с началом В второй фазы, конец Y второй фазы – с началом С третьей фазы, конец третьей фазы Z – c началом первой фазы А. Начала А, В и С фаз подключаются с помощью трех проводов к приемникам.
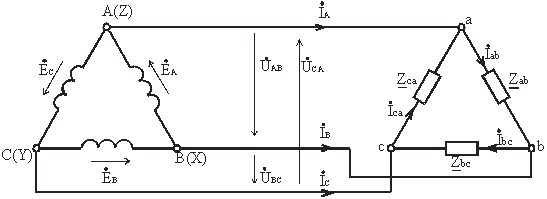
Рис. 3.12
Напряжение между концом и началом фазы при соединении треугольником – это напряжение между линейными проводами. Поэтому при соединении треугольником линейное напряжение равно фазному напряжению.
UЛ = UФ.
Пренебрегая сопротивлением линейных проводов, линейные напряжения потребителя можно приравнять линейным напряжениям источника питания: Uab = UAB, Ubc = UBC, Uca = UCA. По фазам Zab, Zbc, Zca приемника протекают фазные токи İab, İbc и İca. Условное положительное направление фазных напряжений Úab, Úbc и Úca совпадает с положительным направлением фазных токов. Условное положительное направление линейных токов İA, İB и İC принято от источников питания к приемнику.
В отличие от соединения звездой при соединении треугольником фазные токи не равны линейным. Токи в фазах приемника определяются по формулам
İab = Úab / Zab; İbc = Úbc / Zbc; İca = Úca / Zca.
Линейные токи можно определить по фазным, составив уравнения по первому закону Кирхгофа для узлов a, b и c (рис 3.12)
İA = İab - İca; İB = İbc - İab; İC = İca - İbc.
Обычно комплексные сопротивления фаз трехфазных приемников равны между собой:
Za = Zb = Zc = Zejφ.
Такие приемники называют симметричными. Если это условие не выполняется, то приемники называют несимметричными. При этом, если Za = Zb = Zc, то трехфазный приемник называют равномерным, если φa = φb = φc, то однородным.
40. Соединение фаз генератора и приемника звездой. Трехпроводная схема. Симметричная нагрузка. Векторная диаграмма.
Схема соединения:
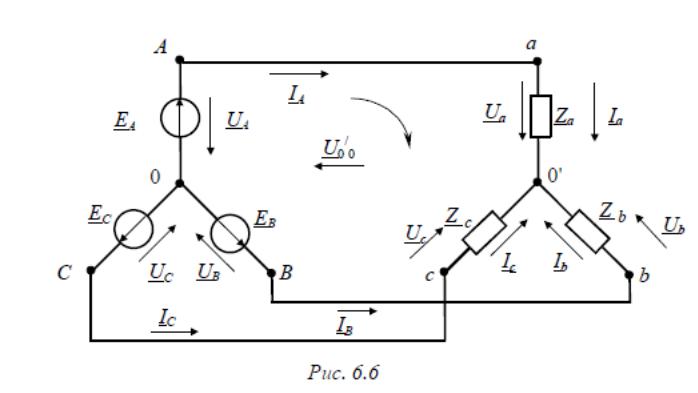
При симметричной нагрузке смещение между нейтральными точками приемника и генератора равно нулю.
Токи находятся по соотношениям:
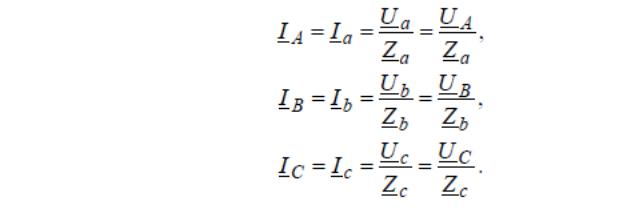
Векторная диаграмма:
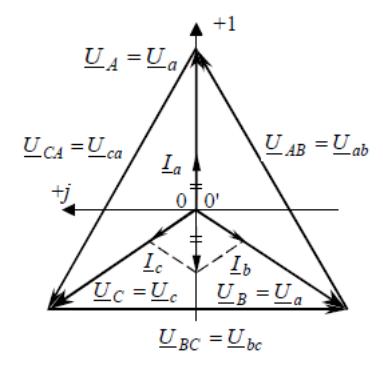 41.
Соединение фаз генератора и приемника
звездой. Трехпроводная схема. Несимметричная
нагрузка. Напряжение смещения. Векторная
диаграмма.
41.
Соединение фаз генератора и приемника
звездой. Трехпроводная схема. Несимметричная
нагрузка. Напряжение смещения. Векторная
диаграмма.

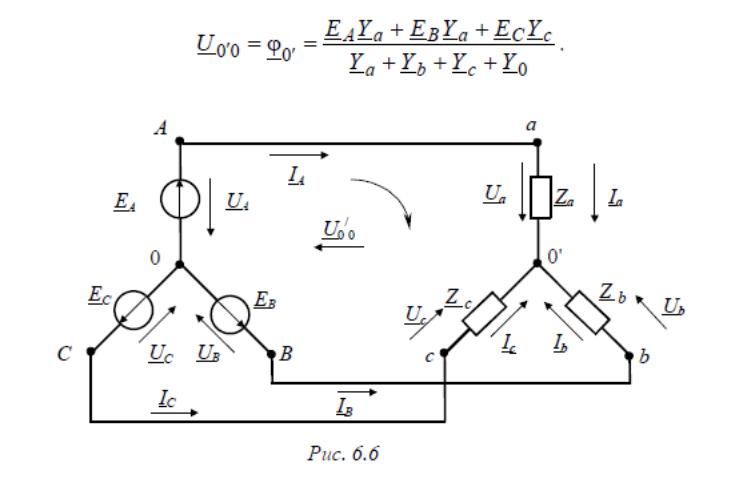
Векторная диаграмма:

42. Соединение фаз генератора и приемника звездой. Четырехпроводная схема. Симметричная нагрузка. Векторная диаграмма.

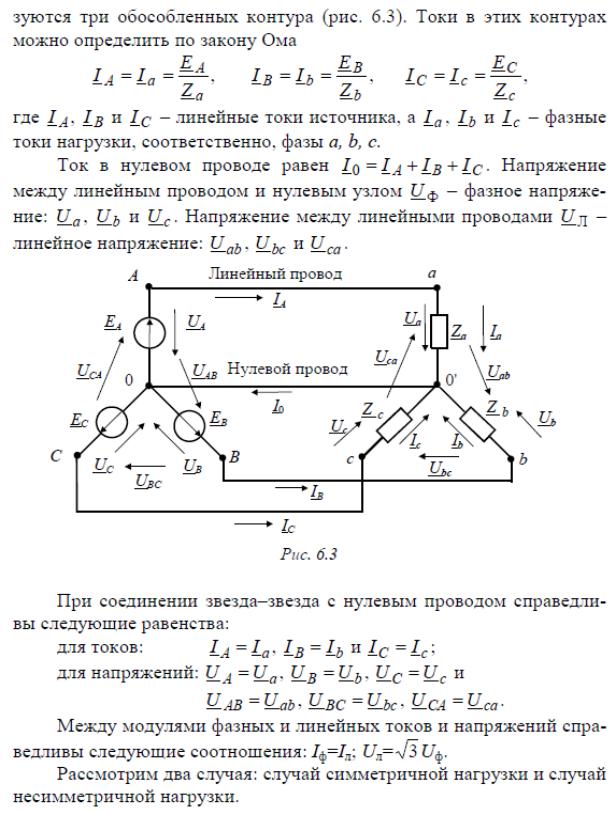
Рассмотрим случай симметричной нагрузки:

43. Соединение фаз генератора и приемника звездой. Четырехпроводная схема. Несимметричная нагрузка. Векторная диаграмма.
Рассмотрим случай несимметричной нагрузки:
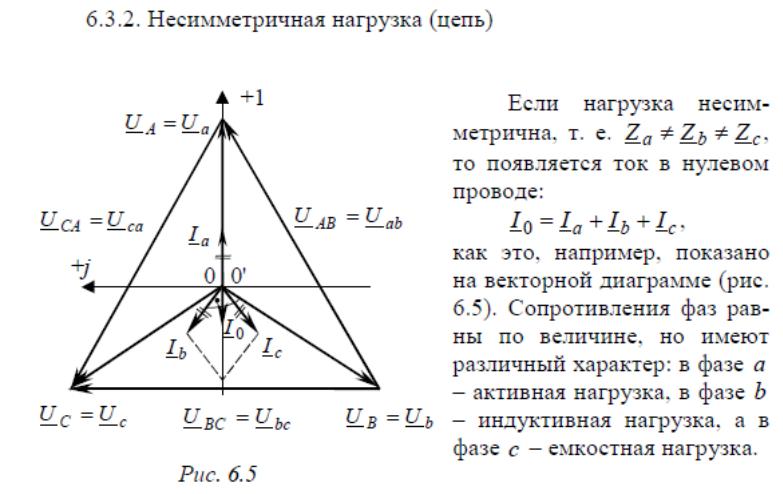
44. Соединение фаз генератора и приемника треугольником. Симметричная и несимметричная нагрузка. Векторная диаграмма.
При соединении источника питания треугольником (рис. 3.12) конец X одной фазы соединяется с началом В второй фазы, конец Y второй фазы – с началом С третьей фазы, конец третьей фазы Z – c началом первой фазы А. Начала А, В и С фаз подключаются с помощью трех проводов к приемникам.
Рис. 3.12
При симметричной нагрузке Zab = Zbc = Zca = Zejφ,
Так как линейные (они же фазные) напряжения UAB, UBC, UCA симметричны, то и фазные токи образуют симметричную систему
İab = Úab / Zab; İbc = Úbc / Zbc; İca = Úca / Zca.
Абсолютные значения их равны, а сдвиги по фазе относительно друг друга составляют 120°.
Линейные токи İA = İab - İca; İB = İbc - İab; İC = İca - İbc;
образуют также симметричную систему токов (рис.3.13, 3.14).

Рис. 3.13
Таким образом, при
соединении треугольником действующее
значение линейного тока при симметричной
нагрузке в
![]() раз
больше действующего значения фазного
тока и UЛ = UФ;
IЛ =
IФ.
раз
больше действующего значения фазного
тока и UЛ = UФ;
IЛ =
IФ.
При равномерной нагрузке фаз расчет трехфазной цепи соединенной треугольником, можно свести к расчету одной фазы.
Несимметричная нагрузка приемника
В общем случае при несимметричной нагрузке Zab ≠ Zbc ≠ Zca. Обычно она возникает при питании от трехфазной сети однофазных приемников. Например, для нагрузки, рис. 3.15, фазные токи, углы сдвига фаз и фазные мощности будут в общем случае различными.

Рис. 3.15
Векторная диаграмма для случая, когда в фазе ab имеется активная нагрузка, в фазе bc – активно-индуктивная, а в фазе ca – активно-емкостная приведена на рис. 3.16, топографическая диаграмма – на рис. 3.17.
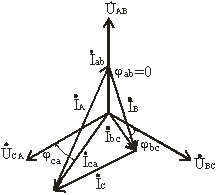
Рис. 3.16
Таким образом, при несимметричной нагрузке симметрия фазных токов İab, İbс, İca нарушается, поэтому линейные токи İA, İB, İC можно определить только расчетом по вышеприведенным уравнениям (3.20) или найти графическим путем из векторных диаграмм (рис. 3.16, 3.17).
Важной особенностью соединения фаз приемника треугольником является то, что при изменении сопротивления одной из фаз режим работы других фаз остается неизменным, так как линейные напряжения генератора являются постоянными. Будет изменяться только ток данной фазы и линейные токи в проводах линии, соединенных с этой фазой. Поэтому схема соединения треугольником широко используется для включения несимметричной нагрузки.
