
- •1. Закон Ома для участка цепи.
- •3. Способы соединения идеализированных элементов и эквивалентные преобразования. Последовательное соединение, параллельное соединение, смешанное соединение.
- •Смешанное соединение – комбинация параллельного и последовательного соединений.
- •4. Преобразование треугольника в эквивалентную звезду, Преобразование звезды в эквивалентный треугольник. Эквивалентные источники напряжения и тока. Понятие о дуальности электрических цепей.
- •5. Законы Кирхгофа для мгновенных величин. Распределение потенциала вдоль цепи с сопротивлениями и источниками напряжения. Потенциальная диаграмма. Баланс мощностей.
- •6. Метод расчета сложных схем с использованием уравнений Кирхгофа, план анализа, пример.
- •7. Метод контурных токов, план анализа, пример.
- •8. Метод узловых потенциалов, план анализа, пример.
- •9. Метод наложения, план анализа, пример.
- •10. Теорема об эквивалентном источнике напряжения. Метод эквивалентного генератора, план анализа, пример.
- •12. Мгновенная и средняя мощности гармонических колебаний.
- •13. Гармонический ток через резистор, напряжение на резисторе. Мгновенная и средняя мощность. Временная и векторная диаграммы тока, напряжения и мощности.
- •14. Гармонический ток через индуктивность, напряжение на индуктивности. Мгновенная и средняя мощность. Временная и векторная диаграммы тока, напряжения и мощности.
- •1 5. Гармонический ток через конденсатор, напряжение на конденсаторе. Мгновенная и средняя мощность. Временная и векторная диаграммы тока, напряжения и мощности.
- •16. Гармонический ток через цепь последовательно соединенных элементов r и l. Векторная диаграмма тока и напряжения.
- •17. Гармонический ток через цепь последовательно соединенных элементов r и с. Векторная диаграмма тока и напряжения.
- •18. Метод комплексных амплитуд. Комплексные амплитуды и комплексные действующие значения. Операции с комплексными значениями.
- •19. Законы Ома и Кирхгофа для комплексных действующих значений.
- •20. Гармонический ток через цепь последовательно соединенных элементов r, l и с. Комплексное сопротивление. Реактивное сопротивление. Векторные диаграммы напряжений и тока.
- •21. Гармонический ток через цепь последовательно соединенных элементов r, l и с. Комплексное сопротивление. Треугольник сопротивлений.
- •22. Гармонический ток в цепи параллельно соединенных элементов r, l и с. Комплексная проводимость. Реактивная проводимость. Векторные диаграммы напряжения и токов.
- •23. Гармонический ток в цепи параллельно соединенных элементов r, l и с. Комплексная проводимость. Треугольник проводимостей.
- •24. Расчет мощности. Активная (средняя), реактивная и полная комплексная мощность. Треугольник мощностей. Коэффициент мощности.
- •25. Баланс мощностей в цепях гармонического тока. Топографическая диаграмма.
- •26. Делители напряжения и тока.
- •27. Согласование источника энергии с нагрузкой.
- •28. Понятие о комплексных частотных характеристиках (кчх). Передаточные и входные комплексные частотные характеристики. Амплитудно-частотные и фазо-частотные характеристики.
- •29. Кчх идеализированных двухполюсных пассивных элементов (сопротивления, индуктивности, емкости).
- •30. Кчх цепей с одним реактивным элементом.
- •32. Резонансный режим работы цепи. Резонанс токов. Нахождение резонансной частоты контура. Частотные характеристики резонансного контура. Векторная диаграмма.
- •33. Разновидности параллельного колебательного контура. Нахождение резонансной частоты.
- •34. Понятие о взаимной индуктивности. Магнитный поток самоиндукции. Магнитный поток рассеяния. Магнитный поток взаимной индукции.
- •36. Трансформатор.
- •37. Генерирование гармонической эдс.
- •38. Трехфазная цепь. Способы представления токов напряжений в фазах трехфазной цепи.
- •45. Расчет мощностей. Активная, реактивная и полная мощность трехфазной цепи. Симметричная и несимметричная нагрузка.
27. Согласование источника энергии с нагрузкой.
Максимальная энергия от источника энергии передается в том случае, если внутреннее сопротивление источника энергии Rs, равно сопротивлению нагрузки Rт.
Простейшее устройство, которое согласует внутреннее сопротивление источника и нагрузки строится на основе согласующего трансформатора
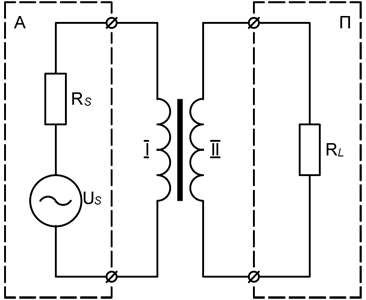
Рис.3. Подключение нагрузки к источнику переменной э.д.с. через согласующий трансформатор
Сила тока в обмотках идеального трансформатора определяется соотношением количества витков первичной и вторичной обмоток:
![]()
I1 - ток во вторичной обмотке трансформатора;
I2 - ток в первичной обмотке трансформатора;
w1 - количество витков первичной обмотки трансформатора;
w2- количество витков вторичной обмотки трансформатора.
В соответствии с теоремой об эквивалентном генераторе часть приведенной на рис.3 схемы, состоящую из активного двухполюсника A и идеального согласующего трансформатора, можно заменить эквивалентным активным двухполюсником с напряжением холостого хода, определяемым выражением
![]()
, и выходным сопротивлением:
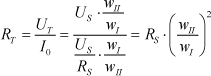
Таким образом, равенства Rт = Rs можно добиться изменением числа витков в первичной или вторичной обмотке согласующего трансформатора.
28. Понятие о комплексных частотных характеристиках (кчх). Передаточные и входные комплексные частотные характеристики. Амплитудно-частотные и фазо-частотные характеристики.
Комплексной частотной характеристикой называется зависимость коэффициента передачи тока или напряжения от частоты. Иногда термин КЧХ применяется к комплексному входному или выходному сопротивлениям исследуемого элемента. Различают 4 вида передаточных функций.


29. Кчх идеализированных двухполюсных пассивных элементов (сопротивления, индуктивности, емкости).
Активное сопротивление не зависит от частоты, поэтому его частотная характеристика постоянна и представляет собой прямую линию. Коэффициент передачи двухполюсника, построенном на активных сопротивлениях постоянен для всех частот.
Сопротивление емкостного элемента обратно пропорционально частоте: XC = 1/ωC;
Сопротивление индуктивного элемента обратно пропорционально частоте: XL = ωL
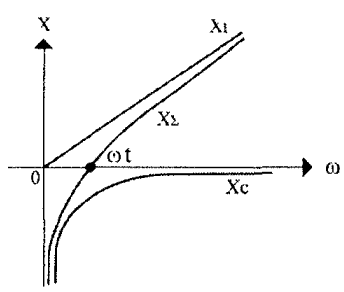
На графике показана зависимость сопротивлений реактивных элементов от частоты, которая на комплексной плоскости является КЧХ реактивных элементов.
30. Кчх цепей с одним реактивным элементом.
Рассмотрим цепь с одним реактивным элементом – емкостью.
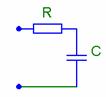
Для данной схемы найдем комплексное входное сопротивление, его модуль и аргумент:
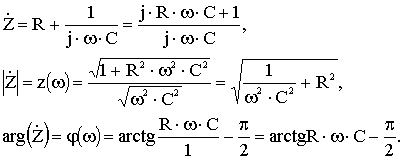 (3.45)
(3.45)
По полученным зависимостям строим соответствующие графики:
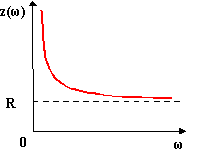
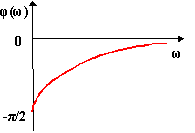
а) б)
а - модуль входной функции; б - аргумент входной функции
Рисунок 3.13 - Частотные характеристики схемы примера 1
Передаточная комплексная функция (коэффициент передачи, системная функция) цепи определяет реакцию цепи на внешнее воздействие и равна отношению выходной величины (напряжение, ток) к входной величине (напряжение, ток), выраженных в комплексной форме.
Различают четыре вида передаточных функций:
1) передаточная
функция по напряжению:
![]()
2) передаточная
функция по току:
![]()
3) передаточное
сопротивление:
![]()
4) передаточная
проводимость:
![]()
В общем виде передаточная функция:
![]() представляется
в виде АЧХ - К(ω) и ФЧХ -
φ(ω)
представляется
в виде АЧХ - К(ω) и ФЧХ -
φ(ω)
31. Резонансный режим работы цепи. Резонанс напряжений. Нахождение резонансной частоты контура. Добротность. Затухание. Частотные характеристики резонансного контура. Полоса пропускания контура. Обобщенная расстройка контура. Абсолютная расстройка контура. Относительная расстройка контура.
Резонансом напряжений называют явление резонанса в участке электрической цепи, содержащей последовательно соединенные индуктивный и емкостной элементы.

Резонансная частота контура находится из условия равенства нулю реактивного сопротивления:
ω0 = 1/√(L∙С)

Затухание – величина, обратная добротности. d = 1/Q
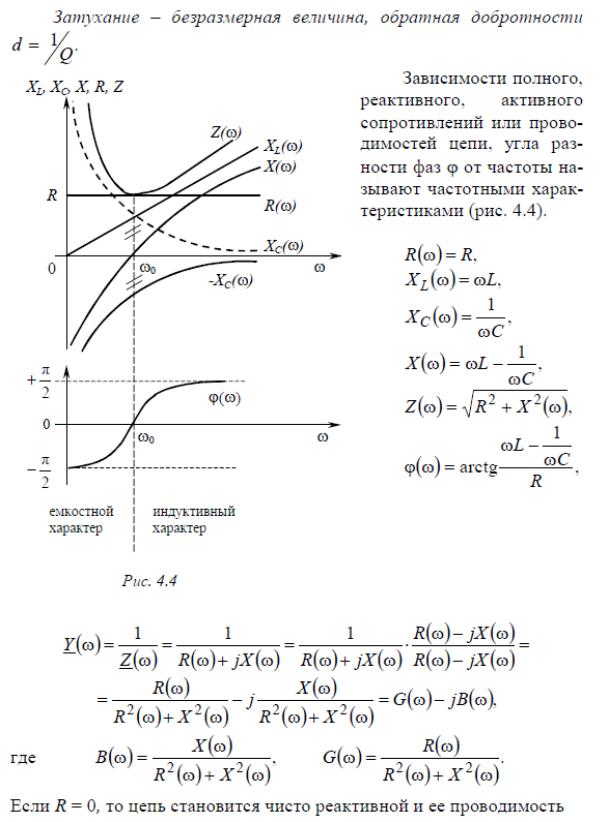
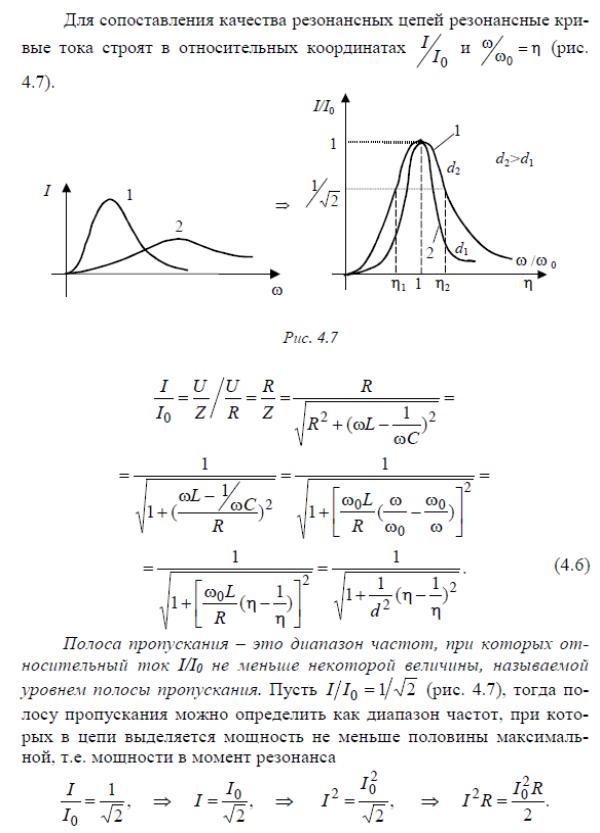

Абсолютная расстройка контура: Δω = |ω – ω0|
Относительная расстройка контура: δω = Δω/ω0
