
Расчетно-графическая работы / РГР 3 / Вариант 5 / РГР №3
.docУфимский государственный авиационный технический университет
Кафедра теоретической механики
Расчетно-графическая работа №3
«Динамика точки»
1064 03 05 07 000
Выполнил: студент группы ИИТ-137
Зинатуллин И.Р.
Проверил: профессор Терешин В.Г.
УФА 2007
Задание №1(Д1). Интегрирование дифференциальных
уравнений движения материальной точки,
находящейся под действием постоянных сил.
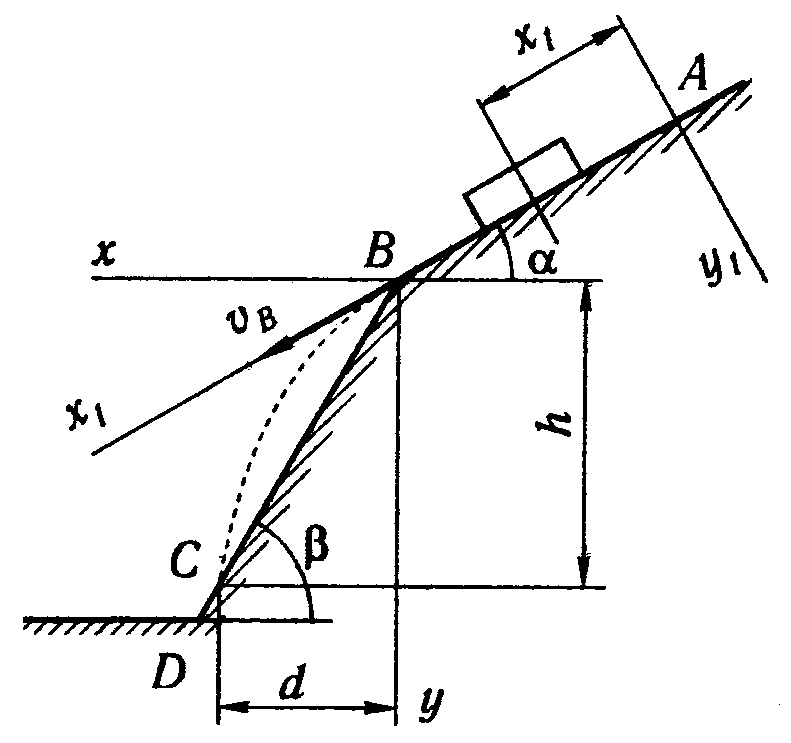
Тело движется из точки А по участку АВ (длиной l) наклонной плоскости, составляющей угол α с горизонтом, в течение τ с. Его начальная скорость vА. Коэффициент трения скольжения тела по плоскости равен f.
В точке В тело покидает плоскость со скоростью vВ и попадает со скоростью vC в точку С плоскости ВD, наклонённой под углом β к горизонту, находясь в воздухе Т с.
При решении задачи тело принять за материальную точку; сопротивление воздуха не учитывать.
Данные:
|
α |
vА, м/с |
l, м |
τ, с |
β |
|
300 |
0 |
9,8 |
3 |
450 |
Определить f и vC.

Решение:
Составим дифференциальное уравнение движения тела на участке АВ:
mx1=Σ Xi1; mx1=G∙sin α - F;
F=f∙N; N=G∙cos α;
mx1=G∙sin α - f∙G∙cos α , или
x1=g∙sin α - f∙g∙cos α ; =>
x1=g(sin α - f∙cos α )t+C1;
x1=[g(sin α - f∙cos α )/2]t2+C1t+C2.
При t=0 x10=0; x10=0, значит
x10=C1; x10=C2; =>
C1=0; C2=0.
Тогда
x1=g(sin α - f∙cos α )t;
x1=[g(sin α - f∙cos α )/2]t2.
Для момента τ, когда тело покидает участок АВ
x1=vВ; x1=l;
vВ= g(sin α - f∙cos α )τ; l=[g(sin α - f∙cos α )/2]τ2,
откуда vВ=2∙l /τ, т.е. vВ≈6,5 (м/с).
Составим дифференциальное уравнение движения тела на участке ВС:
mx=0; my=G.
При t=0 x0=0; y0=0; x0=vB∙cos α; y0=vB∙sin α.
Дважды проинтегрировав эти дифференциальные уравнения, получим:
x=С3; y=gt+С4;
x=C3t+C5; y=gt2/2+C4t+C6.
Тогда
x0=С3; y0=С4;
x0=С5; y0=С6.
Значит
С3=vB∙cos α; С4=vB∙sin α;
С5=0; С6=0.
x=vB∙cos α; y=gt+vB∙sin α;
x=vB∙cos α∙t; y=gt2/2+vB∙sin α∙t.
Уравнение траектории имеет вид:
y=gx2/(2vB2cos2α)+x tg α.
Т.к. β=450, то в момент падения тела h=d, т.е. x=y:
y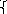 =x,
=x,
y=gx2/(2vB2cos2α)+x tg α.
Решением этой системы будет
x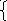 =2,7,
=2,7,
y=2,7.
Из уравнения y=gt2/2+vB∙sin α∙t, найдем время полета Т:
gT2/2+vB∙sin α∙T-y=0;
gT2/2+vB∙sin α∙T-2,7=0,
откуда Т≈0,48(с). _____
vC=√x2+y2 ;
______________________
vC=√( vB∙cos α)2+( gT+vB∙sin α)2,
откуда vC≈9,7(м/с).
С помощью теоремы об изменении кинетической энергии материальной точки найдем коэффициент трения f:
mvB2/2-mvA2/2=Σ Ai=-f∙G∙cos α∙l+ G∙l∙sin α;
mvA2/2=0.
mvB2/2=-f∙G∙cos α∙l+ G∙l∙sin α.
Выразим f:
f=tg α-vB2/(2∙g∙l∙cos α).
f=0,33.
Ответ: f≈0,33, vC≈9,7(м/с).
Задание №2(Д6). Применение основных теорем динамики к исследованию движения материальной точки.
Шарик, принимаемый
за материальную точку, движется из
положения А внутри трубки, ось которой
расположена в вертикальной плоскости.
Найти скорость шарика в положениях В и
С и давление NC
шарика на стенку трубки в положении С.
Трением на криволинейных участках
траектории пренебречь.

Данные:
|
m, кг |
vA, м/с |
, с |
R, м |
f |
α, град |
|
0,1 |
8 |
1,5 |
2,0 |
0,20 |
30 |
Решение:
С помощью теоремы об изменении кинетической энергии материальной точки определим vB и vC:

mvB2/2-mvA2/2=Σ Ai=-f∙N∙l, где l-длина участка АВ;
l=vA∙ -aτ2/2, где а –ускорение.
Ускорение можно определить из выражения:
m∙a=f∙N=f∙m∙g, откуда a=f∙g.
Подставив всё в первоначальное выражение, получим:
mvB2/2-mvA2/2=-f∙m∙g(vA∙τ-f∙g∙τ2/2);
vB2/2-vA2/2=-f∙g(vA∙τ-f∙g∙τ2/2);
vB2=vA2- 2∙f∙g∙τ∙vA+()2=(vA-f∙g∙τ)2;
vB=vA-f∙g∙τ, откуда vB≈5,1(м/с).
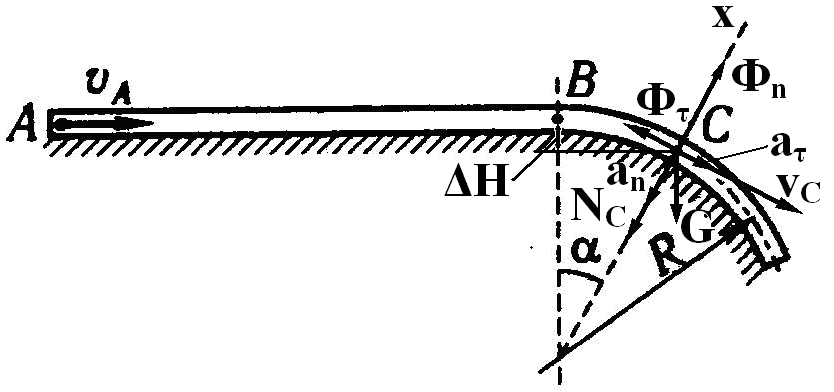
mvС2/2-mvВ2/2=Σ Ai=G∙R-G∙R∙cos α=G∙R(1-cos α);
vС2-vВ2=2∙g∙R(1-cos α);
vС2=2∙g∙R(1-cos α)+vВ2;
_______________
vС=√2∙g∙R(1-cos α)+vВ2, откуда vС≈5,6(м/с).
Для определения NC используем принцип Даламбера:
G+NC+Ф=0;
Ф=Фn+Фτ.
Сумма проекций сил G, NC и Ф на ось x должна быть равна нулю:
NC+G∙cos α-Ф=0;
NC=Ф-G∙cos α=mvC2/R-G∙cos α, откуда NC≈0,72(H).
Ответ: vB≈5,1(м/с), vС≈5,6(м/с),NC≈0,72(H).
