
- •Типовой расчет «Векторная алгебра и аналитическая геометрия»
- •Контрольные варианты к задаче 1.
- •Контрольные варианты к задаче 2
- •Контрольные варианты к задаче 3
- •Контрольные варианты к задаче 4
- •Контрольные варианты к задаче 5
- •Контрольные варианты к задаче 6
- •Контрольные варианты к задаче 7
- •Контрольные варианты к задаче 8
Типовой расчет «Векторная алгебра и аналитическая геометрия»
Задача
1. Если
известны координаты точек
![]() и
и
![]() ,
то координаты вектора
,
то координаты вектора
![]()
Разложение
этого вектора по ортам
![]() :
:
![]()
Длина
вектора находится по формуле
![]() а направляющие косинусы равны
а направляющие косинусы равны
![]() Орт вектора
Орт вектора
![]()
Пример
1. Даны точки
![]()
Разложить
вектор
![]() по ортам
по ортам
![]() и найти его длину, направляющие косинусы,
орт вектора
и найти его длину, направляющие косинусы,
орт вектора
![]() .
Найдем координаты векторов:
.
Найдем координаты векторов:
![]()
![]()
![]() и
и
![]()
Вектор
![]()
![]()
![]()
![]()
![]()
![]()
Контрольные варианты к задаче 1.
Даны
точки А, В и С. Разложить вектор
по ортам
![]() Найти длину, направляющие косинусы и
орт вектора
.
Найти длину, направляющие косинусы и
орт вектора
.
1. |
|
2. |
|
3. |
. |
4. |
|
5. |
|
6. |
|
7. |
|
8. |
|
9. |
|
10. |
|
11. |
|
12. |
|
13. |
|
14. |
|
15. |
|
16. |
|
17. |
|
18. |
|
19. |
|
20. |
|
21. |
|
22. |
|
23. |
|
24. |
|
25. |
|
26. |
|
27. |
|
28. |
|
29. |
|
30. |
|
Задача
2. Если
даны векторы
![]() то скалярное произведение
то скалярное произведение
![]() .
.
Т огда
огда
![]()
![]() ;
проекция вектора
;
проекция вектора
![]() на направление вектора
равна
на направление вектора
равна
![]() ,
условие перпендикулярности ненулевых
векторов выглядит следующим образом:
,
условие перпендикулярности ненулевых
векторов выглядит следующим образом:
![]() Условие
коллинеарности векторов:
Условие
коллинеарности векторов:
![]() .
.
Пример
2. Даны вершины
треугольника
![]() Найти угол при вершине А и проекцию
вектора
Найти угол при вершине А и проекцию
вектора
![]() на сторону АС. С
на сторону АС. С
В
 нутренний
угол при вершине А образован векторами
нутренний
угол при вершине А образован векторами
![]() ,
,
 А
В
А
В
![]()

![]()
![]()
Тогда
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Проекция
на направление вектора
:
![]()
Контрольные варианты к задаче 2
Даны точки А, В и С из задания 1. Найти угол при вершине А и проекцию вектора на сторону АС.
Задача
3. Площадь
параллелограмма, построенного на
векторах
![]()
можно
найти по формуле
![]() а площадь треугольника, построенного
а площадь треугольника, построенного
на
этих векторах:
![]() где
где
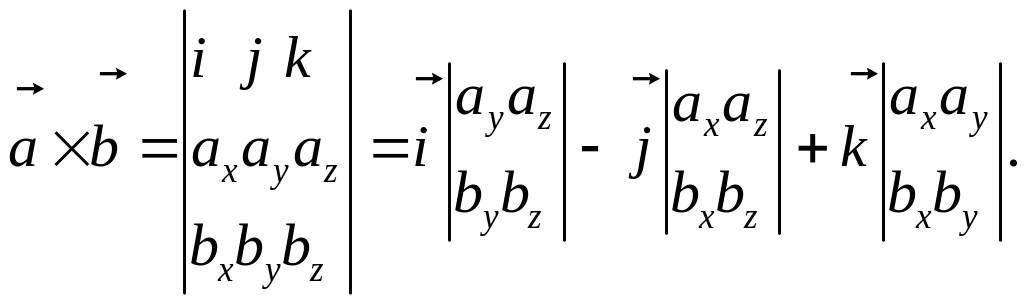
Определитель
второго порядка вычисляется по формуле:
 .
.
Пример
3. Даны вершины
треугольника
![]() Найти его площадь и длину высоты,
опущенной из вершины С.
Найти его площадь и длину высоты,
опущенной из вершины С.
![]() .
Находим векторы
.
Находим векторы
![]()
![]()
![]()
Векторное
произведение

![]()
![]()
![]()
Длина
полученного вектора равна :
![]()
![]()
Так
как
![]() где
где
![]() длина
высоты, опущенной из вершины С на сторону
АВ,
длина
высоты, опущенной из вершины С на сторону
АВ,
![]() .
.
![]()
![]()
