3.8. Термодинамический закон действующих масс (тздм)

Для химической реакции общего вида 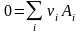(для реагентов _i < 0) изменению состава компонентов 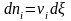при постоянных Т и Р, согласно (3.42), соответствует дифференциальное, а затем и конечное изменение энергии Гиббса.

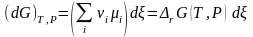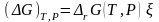, . (3.43)

По химическим потенциалам и стехиометрическим коэффициентам ν_i компонентов, аналогично энтальпии (3.28) и энтропии (3.28'), определена энергия Гиббса реакции

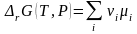. (3.44)

Равновесие в изобарно-изотермическом процессе, в соответствии условием (3.17), определяется нулевой скоростью изменения энергии Гиббса (3.43) в точке её минимума:

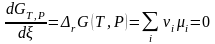. (3.45)

Это общее условие равновесия конкретизируем для газофазной реакции, подставив в него химические потенциалы (3.41) участников:

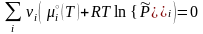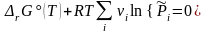, , (3.45')

где 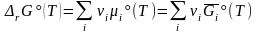(3.44')

- стандартная энергия Гиббса реакции.

Преобразование и эспоненцирование (3.45') приводит к уравнению:

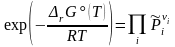(3.46)

Не зависящая от состава реакционной смеси его левая часть называется стандартной константой равновесия:

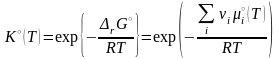. (3.47)

Правую часть (3.46) 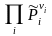назовем стехиометрическим произведением концентраций. В данном случае оно выражено через равновесные значения безразмерных парциальных давлений.

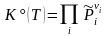( , ν_i < 0 для реагентов). (3.49)

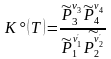('₁A₁+ '₂A₂ = ₃A₃ + ₄A₄). (3.49')

Уравнение, отражающее условие равновесия химической реакции, называется термодинамическим законом действующих масс (ТЗДМ). Форма (3.49) - для реакции общего вида, (3.49') - для 4-х компонентного уравнения реакции в обычной записи.

Поскольку состав системы можно характеризовать разными концентрационными единицами, то различные, в общем случае размерные правые части ТЗДМ, слева должны уравниваться соответствующими константами равновесия. Подстановка связи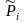 с соответствующей концентрацией в (3.49) позволяет для каждой формы ТЗДМ выразить соответствующую константу равновесия через стандартную К°(Т).

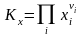, , ; (3.50^х)

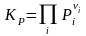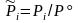, , ; (3.50^Р)

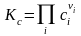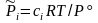, , . (3.50^с)

Здесь  = _i = ₃ + ₄ – '₁ – '₂    – изменение числа молей в реакции, K_x, K_P, K_c – константы равновесия, соответствующие использованию мольных долей x_i, парциальных давлений P_i (атм) и концентраций c_i (моль/м³).

3.9. Направление протекания химической реакции. Использование термодинамического закона действующих масс для расчета состава равновесной смеси

Относительные парциальные давления компонентов реакции до момента их взаимодействия, т.е. в исходном состоянии, отметим дополнительным нижним индексом «0» и выразим энергию Гиббса реакции (3.44) из ТЗДМ (3.45'):

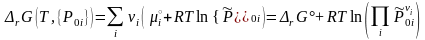(3.51)

Выражение (3.51) впервые получено Вант-Гоффом, а Де-Донде, исходя из необходимого для самопроизвольного протекания процесса отрицательного значения (см. формулу (3.43) в разделе 3.3) сформулировал:

• Если в исходном состоянии энергия Гиббса реакции:

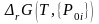  • < 0, то  > 0 и реакция потечет слева направо.

  • > 0, то  < 0 и реакция потечет справа налево.

• Текущие концентрации будут изменяться до достижения своих равновесных значений при 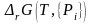= 0.

Расчет равновесного состава при фиксированных Т и Р и при заданной или вычисляемой по энергиям Гиббса веществ константе равновесия сводится к нахождению химической координаты реакции . Для нескольких реакций вместо одного требуется решать уже систему уравнений ТЗДМ с привлечением специализированных компьютерных средств.

Ниже представлено решение для простых, но практически важных реакций. Форма ТЗДМ (3.50^х) соответствует мольным долям x_i.

Пример 1. Зависимость выхода йодистого водорода от соотношения реагентов.

	H2	+ J2	= 2 HJ	 = 0, Kx = K = 45,7 (Т = 718 К)
n0i :	m	n	0
ni = n0i + i :	m–	n–	2	Σni = m + n

x_i = n_i / Σn_i ; ; .

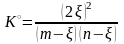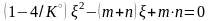Для удобства введены обозначения: 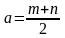, , 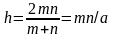A=1−4/K.^◦ Тогда

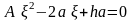
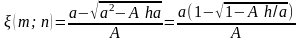
Результаты вычислений при различных исходных количествах йода и водорода (n; m) показывают, что выход по йоду  /n можно повысить за счет избытка водорода!

Пример 2. Расчет выхода аммиака и его зависимость от давления.

			3 H2		+ N2		= 2 NH3		 = -2, Kx= K(P, атм)2, K= 4,21∙10-5 при Т = 720 К
n0i = 'i:		3		1		0
	ni = n0i + i :		3–3		1–		2		ni=2(2-)
	xi = ni/ni:

,

.

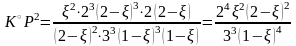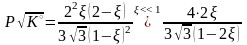
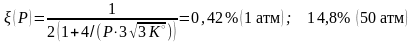Приемлемый выход можно достичь только при повышенных давлениях. На практике аммиак с 30 % -м выходом синтезируют при давлениях около 300 атм.