Теплопроводность через цилиндрическую однослойную стенку

Любая практическая задача теплообмена в итоге сводится к вычислению теплового потока или определения температурного поля.

Для определения температурного поля без внутренних источников теплоты используется дифференциальное уравнение теплопроводности:

, (8)

где – коэффициент температуропроводности, характеризующий скорость изменения температуры в теле, м²/с; с_р – удельная массовая изобарная теплоемкость, Дж/(кг.К);  – плотность, кг/м³; – оператор Лапласа.

В цилиндрических координатах уравнение (8) имеет вид

, (9)

где – радиус-вектор; – угол наклона радиуса-вектора, z – вертикальная координата.

Для стационарного температурного поля в однослойной цилиндрической стенке ( , и ) при λ = idem дифференциальное уравнение теплопроводности принимает вид:

. (10)

Для решения дифференциального уравнения (10) введем новую переменную , тогда уравнение (10) запишется в виде

. (11)

После интегрирования дифференциального уравнения (11), получается

. (12)

Потенцируя выражение (12) и переходя к первоначальной переменной t, получаем

. (13)

Уравнение стационарного температурного поля в цилиндрической однослойной стенке получается после интегрирования выражения (13)

. (14)

Постоянные интегрирования С₁ и С₂ определяются из граничных условий I рода:

при r = r₁ t = t_c1; r = r₂ t = t_c2; (15)

, . (16)

Решение уравнений (16) позволяет найти постоянные интегрирования

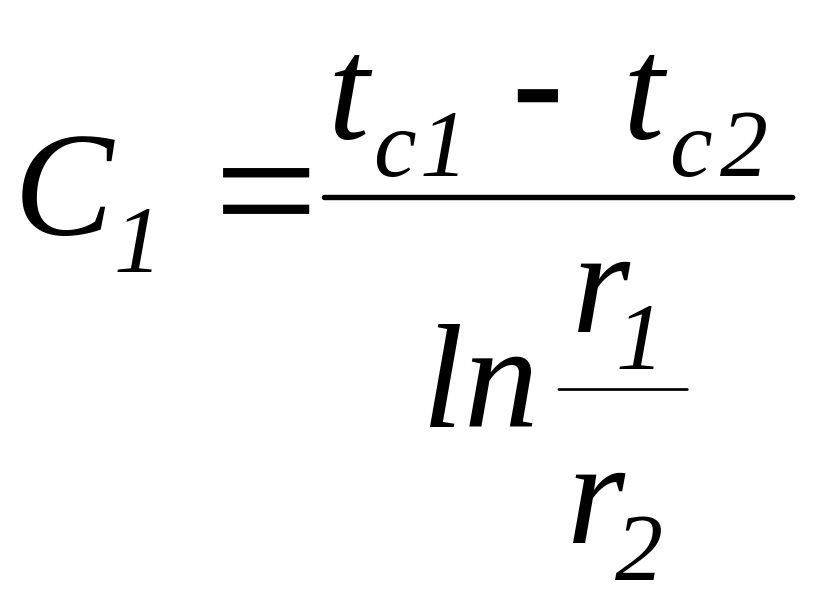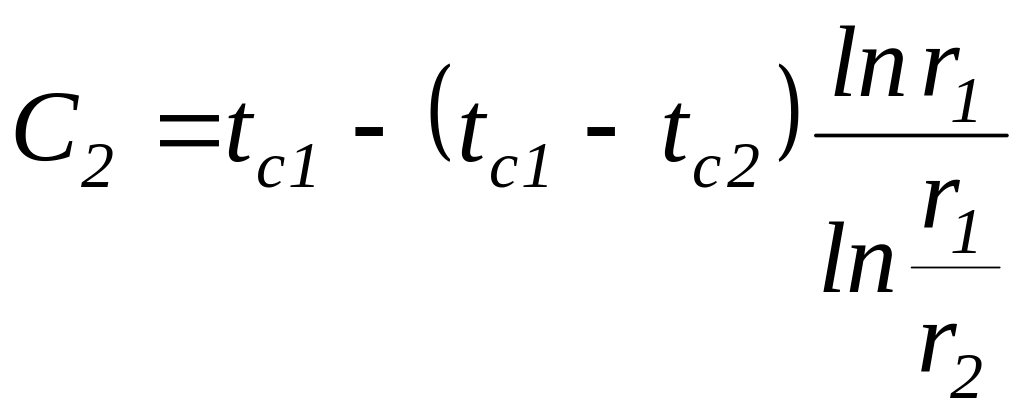, (17)

После подставки полученных значений С₁ и С₂ в уравнение (14), окончательно получается уравнение стационарного одномерного стационарного температурного поля в цилиндрической однослойной стенке (рис. 2):

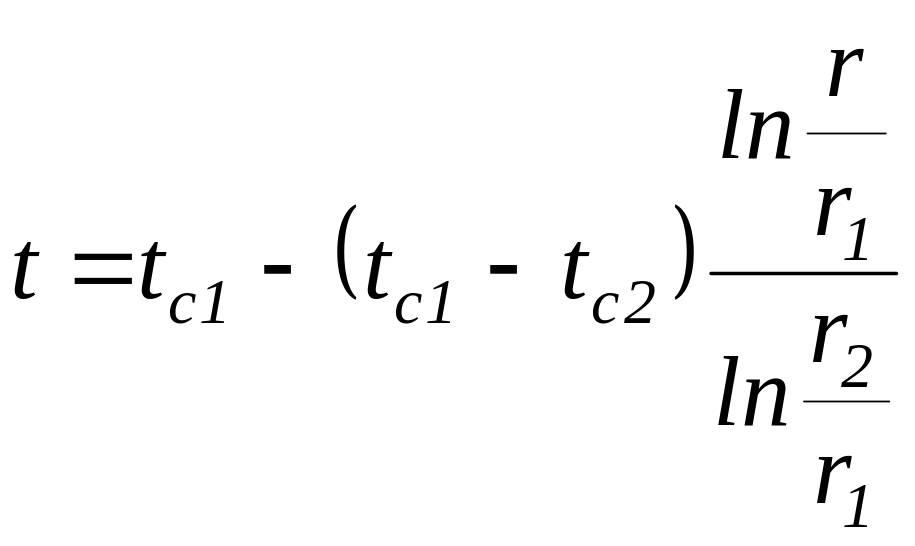, (18)

где t_c1, t_c2 – температуры на внутренней и наружной поверхностях цилиндрической стенки; r₁, r₂ – внутренний и наружный радиусы; r – текущий радиус (r₁  r  r₂).

Полученное выражение температурного поля представляет собой уравнение логарифмической кривой.

Рис. 2. Стационарное температурное поле в цилиндрической однослойной стенке

Так как температура в рассматриваемом случае изменяется только в зависимости от текущего радиуса, то температурный градиент с соотношений (13) и (17) определяется следующем образом:

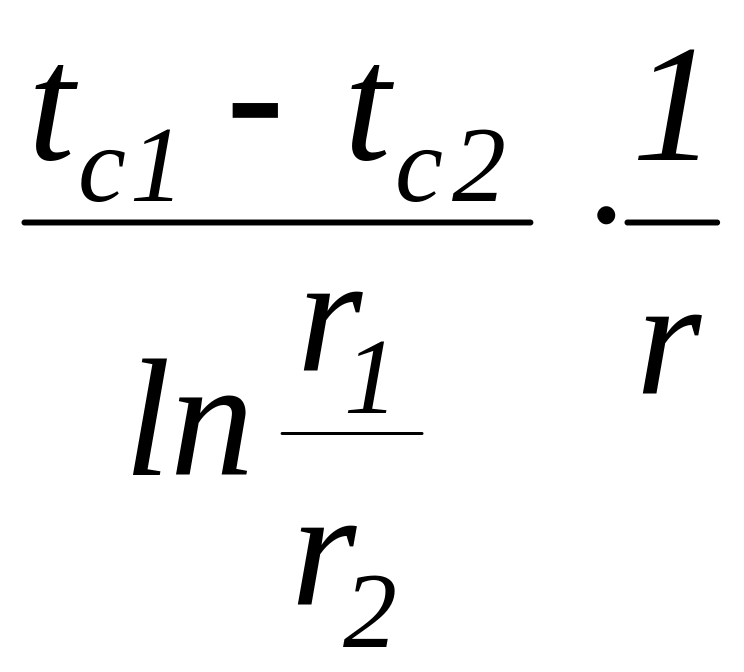. (19)

Тепловой поток, передаваемый теплопроводностью через цилиндрическую однослойную стенку, определяется по закону Фурье (5) с учетом выражения температурного градиента (19) и площади поверхности (F = 2πrl) теплообмена:

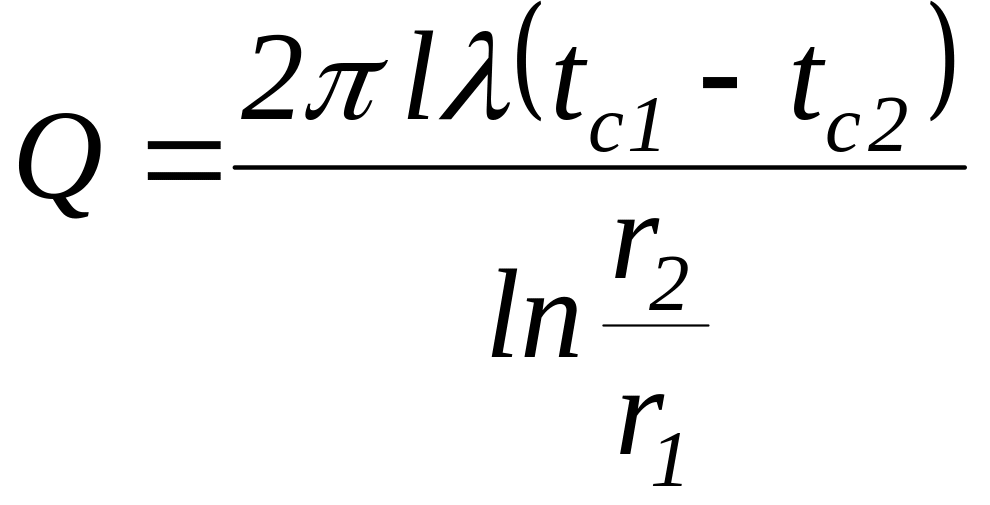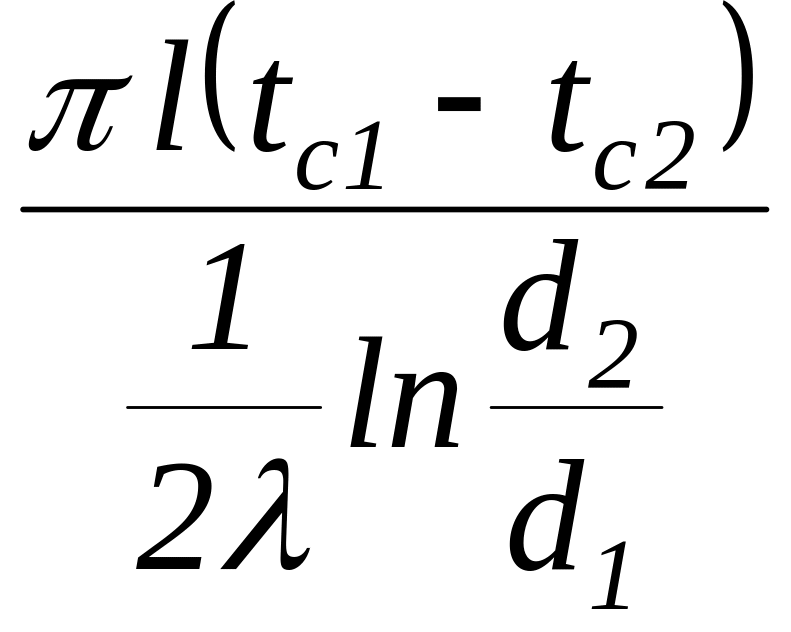= , (20)

Тепловой поток, отнесенный к единице длины цилиндрической стенки l, называется линейной плотностью теплового потока.

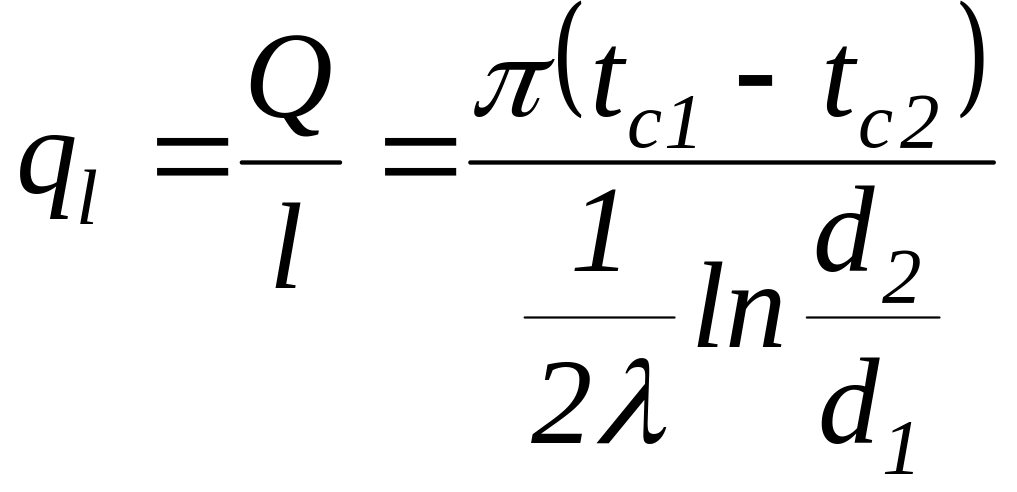, Вm/м (21)

Значения теплового потока Q и линейной плотности теплового потока q_l не меняются во времени и по толщине стенки.

Формулы для определения теплового потока (20) и линейного теплового потока (21) можно представить в виде:

Q = , (22)

где R = , R_l = R/l − полное и удельное линейные термические сопротивления теплопроводности однослойной цилиндрической стенки.

Из соотношений (22) видно, что при стационарной теплопроводности перепад температур на цилиндрической стенке прямо пропорционален термическому сопротивлению и обратно пропорционален величине коэффициента теплопроводности.