Контрольная работа № 1

№ вар-та	№ задач
1	1.00	1.10	1.20	1.30	1.40	1.50	1.60	1.70	1.80	1.90
2	1.01	1.11	1.21	1.31	1.41	1.51	1.61	1.71	1.81	1.91
3	1.02	1.12	1.22	1.32	1.42	1.52	1.62	1.72	1.82	1.92
4	1.03	1.13	1.23	1.33	1.43	1.53	1.63	1.73	1.83	1.93
5	1.04	1.14	1.24	1.34	1.44	1.54	1.64	1.74	1.84	1.94
6	1.05	1.15	1.25	1.35	1.45	1.55	1.65	1.75	1.85	1.95
7	1.06	1.16	1.26	1.36	1.46	1.56	1.66	1.76	1.86	1.96
8	1.07	1.17	1.27	1.37	1.47	1.57	1.67	1.77	1.87	1.97
9	1.08	1.18	1.28	1.38	1.48	1.58	1.68	1.78	1.88	1.98
10	1.09	1.19	1.29	1.39	1.49	1.59	1.69	1.79	1.89	1.99

1.00. Маховик начал вращаться равноускоренно и за промежуток времени  t = 10 с достиг частоты вращения n = 300 мин^1. Определить угловое ускорение  маховика и число N оборотов, которое он сделал за это время.

1.01. Материальная точка движется в плоскости ху согласно уравнениям x=А₁+B₁t+C₁t² и y = А₂+B₂t+ C₂t ², где B₁ = 7 м/с, C₁ = -2 м/с², B₂ = -1 м/с, C₂ = 0,2 м/с². Найти скорость  и ускорение а точки в момент времени t = 5 с.

1.02. Тело брошено под углом  = 30° к горизонту со скоростью ₀ =30 м/с. Каковы будут нормальное а_n, тангенциальное а_ и полное а ускорения тела через время t = 1 с после начала движения? Сопротивлением воздуха пренебречь.

1.03. Из одного и того же места начали равноускоренно двигаться в одном направлении две точки, причем вторая начала свое движение через t = 2 с после первой. Первая точка двигалась с начальной скоростью ₁ = 1 м/с и ускорением а₁ = 2 м/с², вторая - с начальной скоростью ₂ = 10 м/с и ускорением а₂ = 1 м/с². Через какое время t и на каком расстоянии S от исходного положения вторая точка догонит первую?

1.04. Движение точки по окружности радиусом R = 4 м задано уравнением =А+Bt+Сt², где А = 10 м, В = - 2 м/с, С = 1 м/с²;  - криволинейная координата, отсчитанная от некоторой точки, принятой за начальную, вдоль окружности. Найти тангенциальное а_, нормальное а_n и полное а ускорения точки в момент времени t = 2c.

1.05. Точка движется по прямой согласно уравнению x = At + Bt³, где А = 6 м/с,

В = - 0,125 м/с³. Определить среднюю путевую скорость  движения точки в интервале времени от t₁ = 2 с до t₂ = 6 с.

1.06. Точка движется по окружности радиусом R = 10 см с постоянным тангенциальным а_ ускорением. Найти нормальное а_n ускорение точки через время t = 20 с после начала движения, если известно, что к концу N = 5 оборота после начала движения линейная скорость точки  = 10 см/с.

1.07. Тело, брошенное вертикально вверх, находилось на одной и той же высоте h = 3,6 м два раза с интервалом t = 3 с. Пренебрегая сопротивлением воздуха, вычислить начальную скорость ₀ брошенного тела.

1.08. Диск радиусом R = 20 см вращается согласно уравнению  = А + Вt + Сt³, где А = 3 рад, B = - 1 рад/с, С = 0,1 рад/с³. Определить тангенциальное а_, нормальное а_n и полное a ускорения точек на окружности диска для момента времени t = 10 с.

1.09. Вертикально вверх с начальной скоростью ₀ = 20 м/с брошен камень. Через  = 1 с после этого брошен вертикально вверх другой камень с такой же начальной скоростью. На какой высоте h встретятся камни? Сопротивлением воздуха пренебречь.

1.10. Ядро атома распадается на два осколка массами m₁ =1,610^25 кг и m₂=2,410^25 кг. Определить кинетическую энергию Т₂ второго осколка, если кинетическая энергия Т₁ первого осколка равна 18 нДж.

1.11. Шар массой m = 1,3 кг сталкивается с покоящимся шаром большей массы М. В результате прямого, центрального, абсолютно упругого удара шар потерял w = 0,36 своей кинетической энергии. Определить массу М большего шара.

1.12. На рельсах стоит платформа, на которой закреплено орудие без противооткатного устройства так, что ствол его расположен в горизонтальном положении. Из орудия производят выстрел вдоль железнодорожного пути. Масса снаряда m₁ = 10 кг и его скорость при вылете из орудия ₁ = 1 км/с. Масса платформы с орудием и прочим грузом m₂= 20 т. На какое расстояние L откатится платформа после выстрела, если коэффициент сопротивления  = 0,002?

1.13. Шар массой m₁ = 1 кг движется со скоростью ₁ = 4 м/с и сталкивается с шаром массой m₂ = 2 кг, движущимся навстречу ему со скоростью ₂ = 3 м/с. Каковы скорости u₁ и u₂ шаров после удара? Удар считать абсолютно упругим, прямым, центральным.

1.14. Боек свайного молота массой m₁ = 500 кг падает с некоторой высоты на сваю массой m₂ = 120 кг. Определить КПД  удара бойка, считая удар неупругим. Изменением потенциальной энергии сваи при углублении ее пренебречь. Полезной считать энергию, затраченную на вбивание сваи.

1.15. Частица массой m₁ =10^25 кг обладает импульсом р₁ = 510^20 кгм/с. Определить, какой максимальный импульс р₂ может передать эта частица, сталкиваясь упруго с частицей массой m₂ =410^25 кг, которая до соударения покоилась.

1.16. Два неупругих шара массами m₁ = 2 кг и m₂ = 3 кг движутся соответственно со скоростями ₁ = 8 м/с и ₂ = 4 м/с. Определить увеличение U внутренней энергии шаров при их столкновении в случае, когда меньший шар нагоняет больший.

1.17. Из орудия, не имеющего противооткатного устройства, производилась стрельба в горизонтальном направлении. Когда орудие было неподвижно закреплено, снаряд вылетел со скоростью ₁ = 600 м/с, а когда орудию дали возможность свободно откатываться назад, снаряд вылетел со скоростью ₂ = 580 м/с. С какой скоростью  откатилось при этом орудие?

1.18. Два шара массами m₁ = 10 кг и m₂ = 15 кг подвешены на нитях длиной L = 2 м так, что шары соприкасаются между собой. Меньший шар был отклонен на угол  = 60° и выпущен. Определить высоту h, на которую поднимутся оба шара после удара. Удар шаров считать неупругим.

1.19. В деревянный шар массой m₁ = 8 кг, подвешенный на нити длиной L=1,8 м попадает горизонтально летящая пуля массой m₂ = 4 г. С какой скоростью летела пуля, если нить с шаром и застрявшей в нем пулей отклонилась от вертикали на угол  = 3°? Размером шара пренебречь. Удар пули считать прямым, центральным.

1.20. Масса Земли в n = 81,6 раза больше массы Луны. Расстояние L между центрами масс Земли и Луны равно 60,3R (R - радиус Земли). На каком расстоянии r от центра Земли находится точка, в которой суммарная напряженность g гравитационного поля Земли и Луны равна нулю? (напряженность гравитационного поля – отношение силы тяготения к массе тела)

1.21. Какая работа А должна быть совершена при поднятии с земли материалов для постройки цилиндрической дымоходной трубы высотой h = 40 м, наружным диаметром D = 3 м и внутренним диаметром d = 2 м? Плотность  материала принять равной 2800 кг/м³.

1.22. Во сколько раз средняя плотность _з земного вещества отличается от средней плотности _л лунного? Принять, что радиус Земли в n = 3,66 раза больше радиуса Луны, а ускорение свободного падения на поверхности Земли в k = 6,1 раза больше ускорения свободного падения на поверхности Луны.

1.23. Пружина жесткостью k =1 кН/м была сжата на х₁ = 4 см. Какую работу А нужно совершить, чтобы сжатие пружины увеличить до х₂ = 18 см?

1.24. На какую высоту h над поверхностью Земли поднимется ракета, пущенная вертикально вверх, если начальная скорость ₀ ракеты равна первой космической скорости?

1.25. Стальной стержень длиной L=2 м и площадью поперечного сечения S = 2 см² растягивается некоторой силой, причем удлинение х равно 0,4 см. Вычислить потенциальную энергию П растянутого стержня.

1.26. Определить работу А, которую совершат силы гравитационного поля Земли, если тело массой m = 1 кг упадет на поверхность Земли: 1) с высоты h, равной радиусу Земли; 2) из бесконечности? Радиус R Земли и ускорение g свободного падения на поверхности считать известными.

1.27. Гиря, положенная на верхний конец спиральной пружины, стоящей на подставке, сжимает ее на х = 2 мм. На сколько сожмет пружину та же гиря, упавшая на конец пружины с высоты h = 5 см?

1.28. Спутник обращается вокруг Земли по круговой орбите на высоте h = 520 км. Определить период Т обращения спутника. Ускорение g свободного падения у поверхности Земли и ее радиус R считать известными.

1.29. Какую работу А нужно совершить, чтобы растянуть на х = 1 мм стальной стержень длиной L = 1 м и площадью S поперечного сечения, равной 1 см²?

1.30. В центре скамьи Жуковского стоит человек и держит в руках за середину стержень длиной L = 2,4 м и массой m = 8 кг, расположенный вертикально по оси вращения скамьи. Скамья с человеком вращается с частотой n₁ = 1 с^1. С какой частотой n₂ будет вращаться скамья с человеком, если он повернет стержень в горизонтальное положение? Суммарный момент инерции J человека и скамьи равен 6 кгм².

1.31. По горизонтальной плоскости катится диск со скоростью  = 8 м/с. Определить коэффициент сопротивления , если диск, будучи предоставленным самому себе, остановился, пройдя путь S = 18 м.

1.32. На краю горизонтальной платформы, имеющей форму диска радиусом R = 2 м, стоит человек массой m₁ = 80 кг. Масса платформы m₂ = 240 кг. Платформа может вращаться вокруг вертикальной оси, проходящей через ее центр. Пренебрегая трением, найти, с какой угловой скоростью  будет вращаться платформа, если человек будет идти вдоль ее края со скоростью  = 2 м/с относительно платформы.

1.33. Через неподвижный блок массой m = 0,2 кг перекинута невесомая нить, к концам которой прикреплены грузы массами m₁ = 0,3 кг и m₂ = 0,5 кг. Определить силы натяжения T₁ и T₂ нити по обе стороны блока во время движения грузов, если масса блока равномерно распределена по ободу. Трением и проскальзыванием нити по блоку пренебречь.

1.34. Платформа в виде диска радиусом R = 1 м вращается по инерции с частотой n₁ = 6 мин ^1. На краю платформы стоит человек, масса m которого равна 80 кг. С какой частотой n₂ будет вращаться платформа, если человек перейдет в ее центр? Момент инерции J платформы равен 120 кгм². Момент инерции человека рассчитывать как для материальной точки.

1.35. Шарик массой m = 100 г, привязанный к концу нити длиной L₁=1 м, вращается, опираясь на горизонтальную плоскость, с частотой n₁ = 1 с ^1. Нить укорачивается, и шарик приближается к оси вращения до расстояния L₂ = 0,5 м. С какой частотой n₂ будет при этом вращаться шарик? Какую работу А совершит внешняя сила, укорачивая нить? Трением шарика о плоскость пренебречь.

1.36. В центре скамьи Жуковского стоит человек и держит в руках стержень, расположенный вертикально вдоль оси вращения скамьи. Стержень служит осью вращения колеса, расположенного на верхнем конце стержня. Скамья неподвижна, колесо вращается с частотой n₁ = 10 с ^1. Радиус R колеса равен 20 см, его масса m = 3 кг. Определить частоту n₂ вращения скамьи, если человек повернет стержень на угол  = 180⁰? Суммарный момент инерции J человека и скамьи равен 6 кгм². Массу колеса считать равномерно распределенной по ободу.

1.37. Однородный стержень длиной L = 1 м может свободно вращаться вокруг горизонтальной оси, проходящей через один из его концов. В другой конец абсолютно неупруго ударяет пуля массой m = 7 г, летящая перпендикулярно стержню и его оси. Определить массу М стержня, если в результате попадания пули он отклонился на угол  = 60⁰. Скорость ₀ пули принять равной 360 м/с.

1.38. Человек стоит на скамье Жуковского и ловит рукой мяч массой m = 0,4 кг, летящий в горизонтальном направлении со скоростью ₀ = 20 м/c. Траектория мяча проходит на расстоянии r = 0,8 м от вертикальной оси вращения скамьи. С какой угловой скоростью  начнет вращаться скамья Жуковского с человеком, поймавшим мяч, если суммарный момент инерции J человека и скамьи равен 6 кгм²?

1.39. Маховик вращается по закону, выражаемому уравнением  = А + Bt + Сt², где А= 2 рад, B = 16 рад/с, С = - 2 рад/с². Момент инерции J маховика равен 50 кгм². Найти закон, по которому меняется вращающий момент М. Чему равен вращающий момент М при t = = 3 с?

1.40. Найти скорость  течения углекислого газа по трубе, если известно, что за время t = 30 мин через поперечное сечение трубы протекает масса газа m = 0,51 кг. Плотность газа  = 7,5 кг/м³. Диаметр трубы D = 2 см.

1.41. Какой наибольшей скорости  может достичь дождевая капля диаметром d = =0,3 мм, если динамическая вязкость воздуха  = 1,210^5 Пас?

1.42. Смесь свинцовых дробинок с диаметрами d₁ = 3 мм и d₂ = 1 мм одновременно опустили в сосуд с глицерином высотой h = 1 м. На сколько позже упадут на дно дробинки меньшего диаметра по сравнению с дробинками большего диаметра?

1.43. При движении шарика радиусом r₁ = 2,4 мм в касторовом масле ламинарное обтекание наблюдается при скорости ₁ шарика, не превышающей 10 см/с. При какой минимальной скорости ₂ шарика радиусом r₂ = 1 мм в глицерине обтекание станет турбулентным?

1.44. Вода течет по круглой гладкой трубе диаметром d = 5 см со средней по сечению скоростью  = 10 см/с. Учитывая, что критическое значение числа Рейнольдса для потока жидкости в трубе Re_кp = 2300, определить характер течения жидкости.

1.45. Пробковый шарик диаметром d = 6 мм всплывает в сосуде, наполненном касторовым маслом, с постоянной скоростью  = 1,5 см/с. Определить для касторового масла динамическую  и кинематическую  вязкости.

1.46. Струя воды диаметром d = 2 см, движущаяся со скоростью  = 10 м/с, ударяется о неподвижную плоскую поверхность, поставленную перпендикулярно струе. Найти силу F давления струи на поверхность, считая, что после удара о поверхность скорость частиц воды равна нулю.

1.47. Стальной шарик диаметром d = 0,8 см падает с постоянной скоростью  в касторовом масле. Учитывая, что критическое значение числа Рейнольдса для движения шарика в жидкости Re_кp = 0,5, определить характер движения масла, обусловленный падением в нем шарика.

1.48. Давление Р ветра на стену равно 200 Па. Определить скорость  ветра, если он дует перпендикулярно стене. Плотность воздуха  = 1,29 кг/м³.

1.49. Шарик всплывает с постоянной скоростью  в жидкости, плотность ₁ которой в n = 4 раза больше плотности ₂ материала шарика. Во сколько раз сила сопротивления F_c, действующая на всплывающий шарик, больше силы тяжести mg, действующей на этот же шарик?

1.50. Материальная точка массой 310^2 кг движется по окружности радиусом 1,5 м согласно уравнению s = 3 + 2t³ (м). В какой момент времени нормальное а_n ускорение будет равно тангенциальному а_? Определить для этого момента времени полное ускорение а и момент М действующей силы.

1.51. Колесо радиуса 0,2 м с равномерно распределенной по ободу массой 5 кг вращается относительно неподвижной оси, перпендикулярной его плоскости и проходящей через его центр, так, что зависимость угла поворота колеса от времени задается уравнением  = 5 + + 4t² – t³ (рад). Определить для момента времени t = 1 с момент импульса L колеса; момент M действующей силы; кинетическую энергию T колеса.

1.52. Зависимость углового ускорения  колеса, вращающегося относительно неподвижной оси, перпендикулярной к его плоскости и проходящей через его центр, от времени задана уравнением  = 2 + 3t² (с^2). Радиус колеса 0,3 м, масса 20 кг равномерно распределена по ободу. Определить: угловой путь , пройденный за время от t₁ = 1 с до t₂ = 3с; полное число N оборотов, сделанных колесом за это время; линейную скорость  точек на ободе колеса; момент импульса L колеса в момент времени t = 3с ( ₀ = 0).

1.53. Обруч, вся масса которого 1 кг равномерно распределена по ободу, вращается относительно оси, перпендикулярной его плоскости и проходящей через его центр. Радиус обруча 0,1 м. Зависимость момента импульса обруча от времени имеет вид L = 0,05t² (кгм²/с). Определить: угловое ускорение  обруча в момент времени t = 10 с; момент силы M, действующей на обруч при t = 10 с; работу A силы за промежуток времени от t₁ = 1с до t₂ = 2с.

1.54. Материальная точка массой 210^3 кг движется по окружности радиусом 2 м. Ее угловая скорость зависит от времени согласно уравнению  = 0,4t² (c^1). Определить для момента времени t = 2с: силу F_, действующую по касательной к траектории; нормальное а_n, касательное а_ и полное a ускорения точки; кинетическую энергию T.

1.55. В центре неподвижного горизонтального диска, который может вращаться вокруг вертикальной оси, проходящей через его центр, стоит человек и держит в руках велосипедное колесо. Ось колеса направлена вертикально вверх и совпадает с осью скамьи. Радиус колеса 0,3 м, его масса 3 кг равномерно распределена по ободу. Радиус диска 0,5 м, масса диска 60 кг. Определить, с какой угловой скоростью  будет вращаться диск, если человек сообщит колесу угловую скорость 20 c^1 относительно Земли. Моментом инерции человека пренебречь.

1.56. Деревянный стержень массой 2 кг и длиной 1 м, расположенный горизонтально, может вращаться относительно вертикальной оси, проходящей через его конец. В другой конец стержня попадает пуля массой 0,02 кг, летящая со скоростью 600 м/с горизонтально, перпендикулярно стержню. Определить угловую скорость , с которой будет вращаться стержень, если пуля застрянет в нем. Пулю можно считать материальной точкой.

1.57. Грузик массой 0,01 кг, который можно считать материальной точкой, присоединен ниткой длиной 0,1 м к центру диска, вращающегося в горизонтальной плоскости, относительно оси, проходящей через его центр. Радиус диска 0,15 м, масса 0,2 кг. Система имеет угловую скорость ₁ = 10 c^1. Нитка пережигается и грузик откатывается на край диска. Определить угловую скорость ₂ системы, если грузик вращается вместе с диском, удерживаясь на его краю.

1.58. На горизонтальной платформе, вращающейся вокруг вертикальной оси, проходящей через ее центр, стоит человек и держит на вытянутых руках две одинаковые гири массой по 2 кг каждая, при этом расстояние от оси платформы до каждой гири 0,75 м. Платформа вращается, делая 1 об/с. Человек сближает гири так, что их расстояние до оси платформы становится равным 0,4 м, а частота оборотов увеличивается до 1,2 об/с. Определить момент инерции платформы с человеком, считая его постоянным, а гири материальными точками.

1.59. Человек находится на краю неподвижной платформы, которая расположена горизонтально и может вращаться относительно вертикальной оси, проходящей через ее центр. Масса человека 50 кг, масса платформы 70 кг, радиус платформы 5 м. Определить, с какой линейной скоростью относительно платформы начал двигаться человек по ее краю, если при этом платформа вращается с угловой скоростью 0,2 c^1. Считать платформу однородным диском, а человека материальной точкой.

1.60. Платформа в виде диска вращается по инерции вокруг вертикальной оси с частотой n₁ = 15 оборотов в минуту. На краю платформы стоит человек. Когда человек перешел в центр платформы, частота вращения возросла до 25 оборотов в минуту. Масса человека m = 70 кг. Определить массу платформы М. Человека считать точечной массой.

1.61. Шар начинает вращаться относительно оси, проходящей через его центр, с постоянным угловым ускорением  = 0,5 с^2. Определить: момент силы M, которой надо подействовать на шар, чтобы через 10 с после начала движения он приобрел момент импульса L = 90 кгм²/с; работу A этой силы за 10 с.

1.62. Маховое колесо вращается с постоянной угловой скоростью  = 60 с^1 относительно оси, проходящей через его центр. Кинетическая энергия колеса T = 910³ Дж. Определить: за какое время вращающий момент сил М = 30 Нм, приложенный к этому маховику, увеличит его угловую скорость  в два раза; во сколько раз возрастет при этом кинетическая энергия T?

1.63. Шар и диск имеют одинаковую массу и катятся по горизонтальной поверхности без скольжения с одинаковой постоянной скоростью. Кинетическая энергия шара T₁ = 70 Дж. Определить: кинетическую энергию T₂ диска; расстояние S, которое пройдут диск и шар до полной остановки, если на них начнет действовать постоянная сила сопротивления 5 Н.

1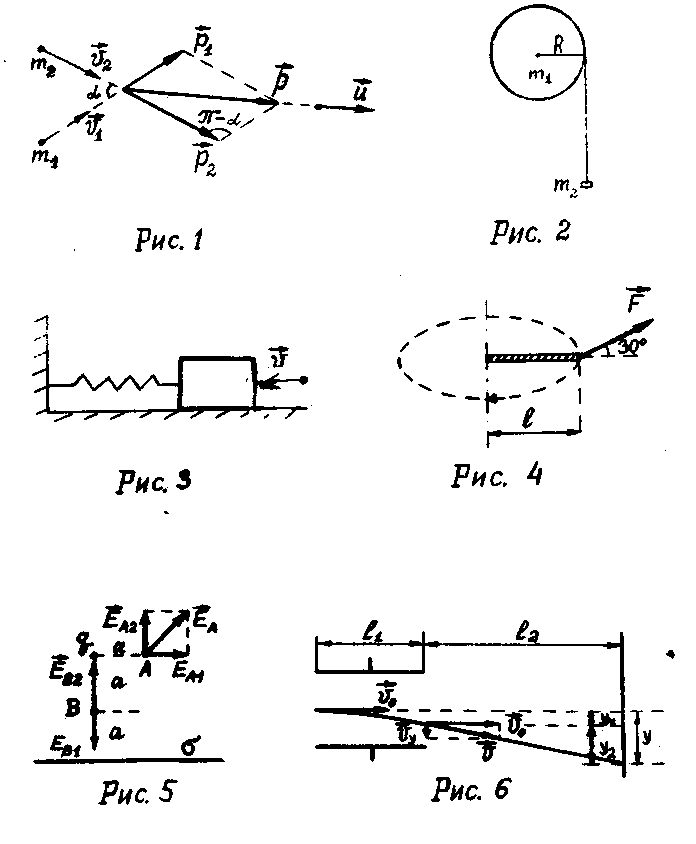 .64. Горизонтальный стержень длиной 0,8 м и массой 1,5 кг вращается относительно вертикальной оси, проходящей через его конец, с угловой скоростью  =50 с^1. В некоторый момент времени к свободному концу стержня приложена тормозящая сила 3,2 Н, линия действия которой горизонтальна и составляет угол 30° с осью стержня. Определить: число N оборотов, сделанных стержнем за 10 с действия силы; момент импульса L стержня через 10 с после начала действия силы.

1.65. Шар, масса которого 1 кг, катится без скольжения со скоростью ₁ = 10 м/с, ударяется о стену и откатывается от нее. При ударе выделяется 44,8 Дж тепла. Определить: скорость ₂ после удара; изменение импульса p шара при ударе.

1.66. Две гири массами 2 кг и 3 кг соединены невесомой нерастяжимой нитью, перекинутой через блок, массой 1 кг. Блок является однородным диском. Определить: ускорение a, с которым движутся гири; силы натяжения T₁ и T₂ нитей; кинетическую энергию E системы через 1 с после начала движения.

1.67. Двум одинаковым маховикам, выполненным в виде однородных дисков радиусом 0,4 м и массой 1000 кг сообщили одинаковую частоту вращения 480 оборотов/мин. Под действием сил трения первый маховик остановился через 1 мин 20 с, а второй маховик сделал до полной остановки 240 оборотов. Определить моменты M₁ и М₂ сил трения, действовавшие на каждый из маховиков, считая их величины постоянными во время вращения.

1.68. Двум одинаковым маховикам, исходно находящимся в покое, сообщили одинаковую угловую скорость  = 63 рад/с. Под действием сил трения первый маховик остановился через одну минуту, а второй сделал до полной остановки 360 оборотов. Определить, для какого маховика тормозящий момент М сил трения был больше и во сколько раз.

1.69. Обруч, вся масса которого распределена равномерно по его окружности, катится по горизонтали со скоростью 2 м/с. Определить, какое расстояние он прокатится вверх по наклонной плоскости до полной остановки, если угол наклона плоскости к горизонту 5⁰?

1.70. Колебания материальной точки происходят согласно уравнению , где А = 8 см,  = /6 с^1. В момент, когда возвращающая сила F в первый раз достигла значения 5 мН, потенциальная энергия П точки стала равной 100 мкДж. Найти этот момент времени t и соответствующую ему фазу  t.

1.71. Тело массой m = 4 кг, закрепленное на горизонтальной оси, совершало колебания с периодом Т₁ = 0,8 с. Когда на эту ось был насажен диск так, что его ось совпала с осью колебаний тела, период Т₂ колебаний стал равным 1,2 с. Радиус R диска равен 20 см, масса его равна массе тела. Найти момент инерции J тела относительно оси колебаний.

1.72. Точка совершает гармонические колебания с циклической частотой 4,0 рад/с. В некоторый момент времени смещение точки от положения равновесия равно 0,25 м, скорость 1 м/с. Написать уравнение колебаний точки. Определить смещение и скорость точки в момент времени t = Т/12. Начальную фазу принять равной нулю.

1.73. Диск радиусом R = 24 см колеблется около горизонтальной оси, проходящей через середину одного из радиусов перпендикулярно плоскости диска. Определить приведенную длину L и период Т колебаний такого маятника.

1.74. Точка совершает колебания по закону . В некоторый момент времени смещение х₁ точки оказалось равным 5 см. Когда фаза колебаний увеличилась в 2 раза, смешение х₂ стало равным 8 см.

Найти амплитуду А колебаний.

1.75. На тонком стержне длиной = 30 см укреплены два одинаковых груза: один - в середине стержня, другой - на одном из его концов. Стержень с грузами колеблется около горизонтальной оси, проходящей через свободный конец стержня. Определить приведенную длину L и период Т простых гармонических колебаний данного физического маятника. Массой стержня пренебречь.

1.76. Материальная точка массой 0,1 г колеблется согласно уравнению (длина — в сантиметрах, время — в секундах). Определить максимальные значения возвращающей силы и кинетической энергии точки.

1.77. Материальная точка массой 0,01 кг совершает гармонические колебания, уравнение которых имеет вид: (длина — в сантиметрах, время — в секундах). Найти возвращающую силу в момент t = 0,1 сек, а также полную энергию точки.

1.78. Тонкий обруч, подвешенный на гвоздь, вбитый горизонтально в стену, колеблется в плоскости, параллельной стене. Радиус R обруча равен 30 см. Вычистить период Т колебаний обруча.

1.79. Полная энергия колеблющегося тела 510⁵ Дж, максимальная сила, действующая на тело, 2,510^3 Н, частота колебании 0,5 Гц, начальная фаза 60°. Написать уравнение колебаний тела. Определить скорость и ускорение тела в момент времени t = Т/6.

1.80. Точка участвует в двух одинаково направленных колебаниях: и , где А₁ = 1 см, A₂ = 2 см,  = 1 с^1. Определить амплитуду А результирующего колебания, его частоту  и начальную фазу ₀. Написать уравнение этого движения.

1.81. Точка совершает одновременно два гармонических колебания, происходящих по взаимно перпендикулярным направлениям и выражаемых уравнениями и , где А₁ = 4 см, А₂ = 8 см,  =  с^1,  = 1 с. Написать уравнение траектории точки.

1.82. В начальный момент времени смещение колеблющейся точки максимально и равно 0,1 м. За 10 колебаний амплитуда уменьшается на 1/10 своей первоначальной величины. Период колебаний равен 0,4 с. Определить коэффициент затухания и логарифмический декремент. Написать уравнение колебаний.

1.83. Уравнение затухающего колебания системы имеет вид: м. Масса системы 0,1 кг. Определить собственную частоту колебаний, коэффициент затуханий, коэффициент сопротивления, логарифмический декремент. Подсчитать амплитуду колебании в момент времени t = 5 с.

1.84. Точка массой 0,02 кг участвует в двух одинаково направленных колебаниях одинаковых частот 2 Гц. Амплитуда первого колебания 0,05 м, начальная фаза /6. Амплитуда второго колебания 0,07 м, начальная фаза /4. Определить: скорость точки в момент времени t = Т/3; полную энергию колебаний.

1.85. Материальная точка массой 0,1 кг участвует в двух одинаково направленных колебаниях, которые заданы уравнениями: см; см. Написать уравнение результирующего колебания. Определить полную энергию точки.

1.86. Материальная точка участвует одновременно в двух взаимно перпендикулярных колебаниях, происходящих согласно уравнениям: и (длина — в сантиметрах, время — в секундах). Определить траекторию точки. Построить траекторию с соблюдением масштаба, указать направление движения точки.

1.87. Период затухающего колебания системы 2 с, логарифмический декремент 1,6; начальная фаза равна 0. В момент времени t = Т/4 смещение равно 5 см. Написать уравнение колебании. Определить число колебаний, по прошествии которых амплитуда убывает в 100 раз.

1.88. Вынужденные колебания описываются дифференциальным уравнением . Определить: частоту вынужденных колебаний; частоту собственных колебаний системы; при какой частоте внешней силы будет наблюдаться резонанс.

1.89. Груз массой 2,5 кг, подвешенный к пружине с коэффициентом жесткости 360 Н/м, совершает вынужденные колебания под действием внешней силы H. Определить амплитуду вынужденных колебаний груза. Трением пренебречь.

1.90. От источника колебаний распространяется волна вдоль прямой линии. Амплитуда А колебаний равна 10 см. Как велико смещение  точки, удаленной от источника на х=3/4, в момент, когда от начала колебаний прошло время t = 0,9 T?

1.91. Определить длину  бегущей волны, если в стоячей волне расстояние между первой и седьмой пучностями равно 15 см.

1.92. Волна распространяется в упругой среде со скоростью  = 100 м/с. Наименьшее расстояние х между точками среды, фазы колебаний которых противоположны, равно 1 м. Определить частоту  колебаний.

1.93. Плоская бегущая акустическая волна представлена уравнением м. Определить частоту колебаний, скорость и длину волны.

1.94. Уравнение незатухающих колебаний источника имеет вид: м. Длина волны 15 м. Написать уравнение плоской волны. Определить: смещение точки среды, находящейся на расстоянии 20 м от источника в момент времени 0,01 с; разность фаз колебаний точек, расположенных на расстоянии 15 м и 20 м от источника.

1.95. Плоская волна, возбуждаемая вибратором, колеблющимся по закону м, распространяется со скоростью 10 м/с. Написать уравнение плоской волны. Определить длину волны и период. Определить в момент t = 0,1 с смещение точки среды, находящейся на расстоянии 10,25 м от вибратора.

1.96. Уравнение плоской волны, распространяющейся в стержне сечением 10 см², имеет вид: м. Определить: частоту колебаний; длину волны; скорость распространения волны в стержне. Плотность материала стержня 410³ кг/м³.

1.97. Источник колебаний с периодом 10^2 с и амплитудой 510^4 м посылает волну, распространяющуюся в среде со скоростью 300 м/с. Определить длину плоской волны. Написать уравнение волны. Определить максимальную колебательную скорость частиц среды.

1.98. В стальном стержне распространяется плоская продольная волна от источника, уравнение колебаний которого задано в виде: м. Модуль Юнга стали 210¹¹Н/м²; плотность стали 810³ кг/м³. Написать уравнение волны. Определить длину волны.

1.99. Найти скорость  распространения продольных упругих звуковых колебаний в меди.

МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА