
- •Казанский кооперативный институт (филиал)
- •Экономико-математические методы и модели лекционный материал
- •Введение
- •Тема 1. Математическое моделирование и анализ экономических процессов. Основные представления о математических моделях.
- •Тема 2. Методы и модели оптимального планирования хозяйственной деятельности
- •Тема 3. Оптимальное планирование перевозок товаров. (Транспортная задача, транспортный метод).
- •Формулировка транспортной задачи.
- •Математическая модель транспортной задачи.
- •Необходимое и достаточное условия разрешимости транспортной задачи.
- •Свойство системы ограничений транспортной задачи.
- •Опорное решение транспортной задачи.
- •Метод вычеркивания
- •Методы построения начального опорного решения. Метод северо-западного угла.
- •Метод минимальной стоимости.
- •Переход от одного опорного решения к другому.
- •Означенный цикл.
- •Распределительный метод.
- •Метод потенциалов.
- •Особенности решения транспортных задач с неправильным балансом.
- •Алгоритм решения транспортной задачи методом потенциалов.
- •Транспортная задача по критерию времени.
- •Тема 4. Принятие решений
- •Методы принятия решений
- •Матрица выйгрышей
- •Матрица Рисков
- •2. Принятие решений в условиях частичной неопределенности (в условиях коммерческого риска)
- •Тема 5. Модель системы массового обслуживания
- •Системы массового обслуживания
- •Основные понятия теории массового обслуживания
- •1.7. Система массового обслуживания с отказами
- •8. Одноканальная система массового обслуживания с неограниченной очередью
- •1.10. Система массового обслуживания с ограниченной очередью
- •1.10.1. Одноканальная смо с ограниченной очередью
- •1.10.2 Многоканальная смо с ограниченной очередью
- •Тема 6. Основные понятия и задачи метода сетевого планирования и управления
- •Основные понятия и задачи.
- •Проект реконструкции торгового центра
- •Тема 7. Экономико-математические методы и модели изучения и прогнозирования спроса.
- •1) Исследователь вносит гипотезу о структуре ящика
- •2) Определение неизвестных коэффициентов a0 и a1 модели
- •3) Проверка
- •Линейная множественная модель
- •Тема 8. Модели управления запасами
- •Модели управления запасами.
- •I. Детерминированные модели управления запасами.
- •1.Простейшая модель оптимального размера заказа.
- •2. Модель оптимального размера заказа с фиксированным временем его выполнения.
- •4. Модель оптимального размера заказа с дефицитом.
- •5. Модель оптимального размера с количественными скидками.
- •II. Стохастическая модель
- •6. Дискретная стохастическая модель оптимизации начального запаса.
- •Примеры
- •Тема 8. Балансовая модель. Балансовый метод.
- •Решение балансовых уравнений с помощью обратной матрицы. Коэффициенты полных затрат.
- •Полные внутрипроизводственные затраты.
- •Полные затраты труда капиталовложений
- •Экономико-математические методы и модели лекционный материал
- •420045 Республика Татарстан, г. Казань,
Тема 3. Оптимальное планирование перевозок товаров. (Транспортная задача, транспортный метод).
Вопросы:
Формулировка открытой и закрытой транспортной модели.
Методы составления первоначального плана перевозок
Экономические задачи, решаемые транспортным методом.
Оптимизация транспортных перевозок.
Метод потенциалов.
,,Транспортная задача” объединяет в себе широкий круг задач с единой математической моделью. Классическая транспортная задача – задача о наиболее экономном плане перевозок однородного продукта или взаимозаменяемых продуктов из пунктов производства в пункты потребления, встречается чаще всего в практических приложениях линейного программирования. Линейное программирование является одним из разделов математического программирования – области математики, разрабатывающей теорию и численные методы решения многомерных экстремальных задач с ограничениями.
В зависимости от способа представления условий транспортной задачи она может быть представлена в сетевой (схематичной) или матричной (табличной) форме. Транспортная задача может также решаться с ограничениями и без ограничений.
Формулировка транспортной задачи.
Однородный
груз сосредоточен у m
поставщиков в объемах
 .
Данный груз необходимо доставить n
потребителям в объемах
.
Данный груз необходимо доставить n
потребителям в объемах
 .
Известны
.
Известны
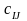 ,
i=1,2,,…,m,
j=1,2,…,n-
стоимости перевозки единицы груза от
каждого I-го поставщика
каждому j-му потребителю.
Требуется составить такой план перевозок,
при котором запасы всех потребителей
полностью удовлетворены и суммарные
затраты на перевозку всех грузов
минимальны.
,
i=1,2,,…,m,
j=1,2,…,n-
стоимости перевозки единицы груза от
каждого I-го поставщика
каждому j-му потребителю.
Требуется составить такой план перевозок,
при котором запасы всех потребителей
полностью удовлетворены и суммарные
затраты на перевозку всех грузов
минимальны.
Исходные данные транспортной задачи обычно записываются в таблице (таб1.1).
-



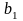

…




…
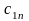


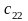
…

…
…
…
….
….

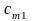

…

Таблица1.1.

 Исходные данные задачи могут быть
представлены также в виде вектора
запасов поставщиков А=(
),
вектора запросов потребителей
Исходные данные задачи могут быть
представлены также в виде вектора
запасов поставщиков А=(
),
вектора запросов потребителей
В=(
)
и матрицы стоимостей
 .
.
В транспортных задачах под поставщиками и потребителями понимаются различные промышленные и сельскохозяйственные предприятия, заводы, фабрики, слады, магазины и т.д. Однородными считаются грузы, которые могут быть перевезены одним видом транспорта. Под стоимостью перевозок понимаются тарифы, расстояния, время, расход топлива и т.п.
Математическая модель транспортной задачи.
Переменными
(неизвестными) транспортной задачи
являются
 i=1,2,,…,m,
j=1,2,…,n –
объемы перевозок от каждого i-го
поставщика каждому j-му
потребителю. Эти переменные можно
записать в виде матрицы перевозок
i=1,2,,…,m,
j=1,2,…,n –
объемы перевозок от каждого i-го
поставщика каждому j-му
потребителю. Эти переменные можно
записать в виде матрицы перевозок
 .
.
Так как произведение
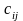
 определяет затраты на перевозку груза
от i-го поставщика j-му
потребителю, то суммарные затраты на
перевозку всех грузов равны
определяет затраты на перевозку груза
от i-го поставщика j-му
потребителю, то суммарные затраты на
перевозку всех грузов равны

 .
По условию задачи требуется обеспечить
минимум суммарных затрат. Следовательно,
целевая функция имеет вид
.
По условию задачи требуется обеспечить
минимум суммарных затрат. Следовательно,
целевая функция имеет вид


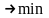 .
.
Система ограничений задачи состоит из двух групп уравнений. Первая группа из m уравнений описывает тот факт, что запасы всех m поставщиков вывозятся полностью:
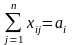 ,
i=1,2,…,m.
,
i=1,2,…,m.
Вторая группа из n уравнений выражает требование полностью удовлетворить запросы всех n потребителей:
 ,
j=1, 2, … , n.
,
j=1, 2, … , n.
Учитывая условие неотрицательности объемов перевозок, математическую модель задачи можно записать так:
, (1)
, i=1,2,…,m , (2)
, j=1, 2, … , n, (3)
 ,
i=1,2,,…,m,
j=1,2,…,n (4)
,
i=1,2,,…,m,
j=1,2,…,n (4)
В рассмотренной модели транспортной
задачи предполагается, что суммарные
запасы поставщиков равны суммарным
запросам потребителей, т.е.
 .
.
Такая задача называется задачей с правильным балансом, а ее модель – закрытой. Если же это равенство не выполняется, то задача называется задачей с неправильным балансом, а ее модель – открытой.
Математическая формулировка
транспортной задачи такова: найти
переменные задачи
 ,
i=1,2,,…,m,
j=1,2,…,n,
удовлетворяющие системе ограничений
(2), (3), условиям неотрицательности (4) и
обеспечивающие минимум целевой функции
(1).
,
i=1,2,,…,m,
j=1,2,…,n,
удовлетворяющие системе ограничений
(2), (3), условиям неотрицательности (4) и
обеспечивающие минимум целевой функции
(1).
Математическая модель транспортной задачи может быть записана в векторном виде. Для этого рассмотрим матрицу А системы уравнений-ограничений задачи (2), (3):
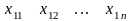

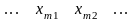



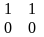






.……………………………………………………
А =




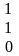
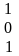
 (6).
(6).
……………………………………………………
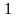
Сверху над каждым столбцом матрицы
указана переменная задачи, коэффициентами
при которой являются элементы
соответствующего столбца в уравнениях
системы ограничений. Каждый столбец
матрицы А, соответствующий переменной
,
является вектором-условием задачи и
обозначается через
 .
Каждый вектор имеет всего m+n
координат, и только две из них, отличные
от нуля, равны единице. Первая единица
вектора
стоит на i-м месте, а вторая
– на (m+j)-м
месте, т.е.
.
Каждый вектор имеет всего m+n
координат, и только две из них, отличные
от нуля, равны единице. Первая единица
вектора
стоит на i-м месте, а вторая
– на (m+j)-м
месте, т.е.
Номер
корди-
наты


 =
=

 ;
;
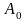 =
=
 .
.
Обозначим через вектор ограничений (правых частей уравнений (2), (3)) и представим систему ограничений задачи в векторном виде. Тогда математическая модель транспортной задачи запишется следующим образом:
, (7)
 =
,
(8)
=
,
(8)
, i=1,2,,…,m, j=1,2,…,n (9)
