
Яблонский Д11 вариант 12
.docД-11. Исследование поступательного и вращательного движений твердого тела.
Механическая система состоит из механизма (колёс 1 и 2) и груза 3. К колесу 1 приложена движущая сила Р = P(t). Время t отсчитывается от некоторого момента (t = 0), когда угловая скорость колеса 1 равна ω0. Момент сил сопротивления ведомого колеса 2 равен Мс. Другие силы сопротивления движению системы не учитывать. Массы колёс 1 и 2 равны т1 и т2, а масса груза - m3. Радиусы больших и малых окружностей колёс R1 ,r1, R2, r2. Относительно неподвижных осей колёс 1 и 2 заданы их радиусы инерции ix1, ix2.
Найти уравнение φ1 = f(t) движения колеса 1 системы. Определить также натяжение нити Т в заданный момент времени t1. Найти, кроме того, окружное усилие S колёс 1 и 2 в точке их касания.
Дано: m1 = 100кг, m2 = 200кг, m3 = 600кг, R1 = 0.30м, r1 = 0.20м, R2 = 0.60м,
ix1
= 0.20![]() м,
ix2
= 0.60м, Р = 5700 + 50t (H), Мс
= 1500Нм, g = 9.81м/с2, ω10
= 2рад/с, t1
= 2с.
м,
ix2
= 0.60м, Р = 5700 + 50t (H), Мс
= 1500Нм, g = 9.81м/с2, ω10
= 2рад/с, t1
= 2с.
Найти: φ1 = f(t), T, S.
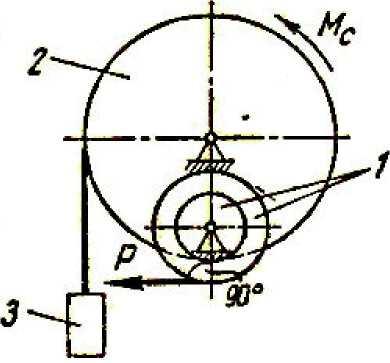
Рис.Д11.1
Решение
В данной механической системе колеса 1 и 2 механизма вращаются вокруг неподвижных осей, а поднимаемый груз 3 совершает поступательное движение.
Напишем дифференциальные уравнения движения каждого из этих трех тел, для чего отделим одно от другого, разрезав нить, удерживающую груз 3, и разъединив колеса 1 и 2 в точках соприкасания зубцов (рис. Д11.1).
К колесу 1 механизма
приложены сила тяжести
![]() движущая сила
движущая сила![]() ,
составляющие реакции подшипника
,
составляющие реакции подшипника
![]() ,
,
![]() ,
окружное усилие
,
окружное усилие
![]() и нормальная реакция
и нормальная реакция
![]() колеса 2.
колеса 2.
К колесу 2 механизма
приложены сила тяжести
![]() ,
момент сил сопротивления Мс,
составляющие реакции подшипника
,
момент сил сопротивления Мс,
составляющие реакции подшипника
![]() ,
,
![]() ,
натяжения
,
натяжения
![]() нити, к которой подвешен груз 3, окружное
усилие
нити, к которой подвешен груз 3, окружное
усилие
![]() и нормальная реакция
и нормальная реакция
![]() колеса 1.
колеса 1.
К грузу 3 приложены
сила тяжести
![]() ,
и натяжение нити
,
и натяжение нити
![]() .
.
Очевидно,
![]() .
Составим дифференциальное уравнение
вращательного движения колеса 1 вокруг
оси x1:
.
Составим дифференциальное уравнение
вращательного движения колеса 1 вокруг
оси x1:
![]() ,
,
здесь
![]() – главный момент внешних сил, приложенных
к колесу 1, относительно оси вращения
x1:
– главный момент внешних сил, приложенных
к колесу 1, относительно оси вращения
x1:
![]() .
.
(Момент от силы Р
приводит в движение колесо 1 и поэтому
принят положительным, а момент, создаваемый
окружным усилием
![]() препятствует вращению колеса 1 и,
следовательно, отрицателен.)
препятствует вращению колеса 1 и,
следовательно, отрицателен.)
Дифференциальное уравнение вращательного движения колеса 1 примет вид
![]() (1)
(1)
Составим дифференциальное уравнение вращательного движения колеса 2 вокруг оси x2 :
![]()
здесь
![]() – главный момент внешних сил, приложенных
к колесу 1, относительно оси вращения
x1:
– главный момент внешних сил, приложенных
к колесу 1, относительно оси вращения
x1:
![]() .
.
(Момент, создаваемый
окружным усилием
![]() приводит в движение, колесо 2 и поэтому
принят положительным, а момент силы
натяжения нити
приводит в движение, колесо 2 и поэтому
принят положительным, а момент силы
натяжения нити
![]() и момент сил сопротивления Мс
препятствуют движению колеса 2 и,
следовательно, отрицательны.)
и момент сил сопротивления Мс
препятствуют движению колеса 2 и,
следовательно, отрицательны.)
Дифференциальное уравнение вращательного движения колеса 2 имеет вид
![]() (2)
(2)
Составим дифференциальное уравнение поступательного движения груза 3:
![]()
Здесь
![]() –
проекция главного вектора внешних сил,
приложенных к грузу 3, на ось у, направленную
в сторону движения груза, т.е. вверх:
–
проекция главного вектора внешних сил,
приложенных к грузу 3, на ось у, направленную
в сторону движения груза, т.е. вверх:
![]() .
.
Дифференциальное уравнение поступательного движения груза 3
![]() (3)
(3)
В уравнениях (1),
(2), (3) неизвестными являются силы Т' =
Т и S1 = S2 = S, а также функции
![]() ,
,
![]() и
и
![]() – угловые ускорения колес 1, 2 и ускорение
груза 3 соответственно.
– угловые ускорения колес 1, 2 и ускорение
груза 3 соответственно.
Но указанные функции связаны между собой соотношениями
 (4)(5)
(4)(5)
так, что в трех
уравнениях - три неизвестные: Т, S,
![]() .
.
Выразим
![]() из (4):
из (4):
![]() и подставим в (1):
и подставим в (1):
![]() (6)
(6)
Исключим из
дифференциального уравнения (2) силу Т,
для чего выразим Т (Т’ = Т) из (3):
![]() .
Учитывая (5), напишем
.
Учитывая (5), напишем
![]() .
.
Тогда (2) приобретает вид
![]() (7)
(7)
Исключим S(S = S1 = S2) из (6) и (7), для чего умножим (6) на R2, a (7) - на r1:
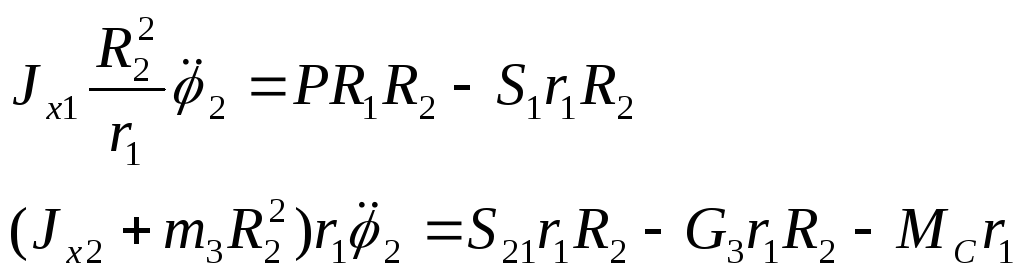
Сложив соответствующие части полученных уравнений, имеем
 (8)
(8)
Выражение (8) определяет в общем виде угловое ускорение колеса 2 механизма. Учитывая соотношение (4), из (8) получим выражение в общем виде для углового ускорения колеса 1:
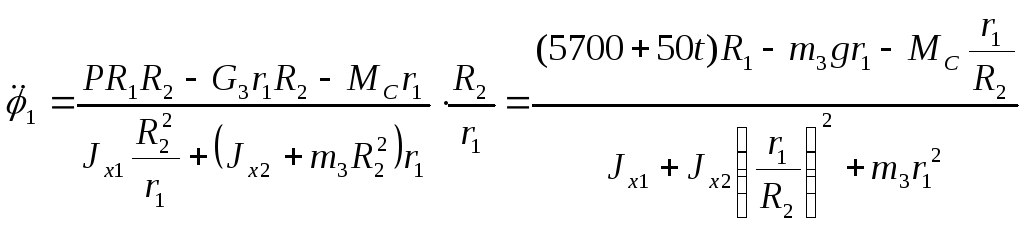 (9)
(9)
Здесь G3 = m3g, g -ускорение свободного падения. Моменты инерции колес 1 и 2 относительно осей x1 и x2
![]() (10)
(10)
Произведём вычисления по формулам (10) и (9), учитывая исходные данные:
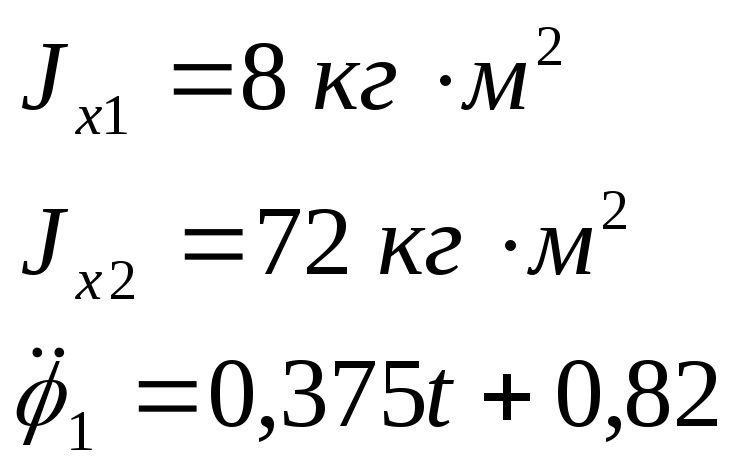 (11)
(11)
Интегрируем это
уравнение дважды, используя следующие
начальные условия задачи: t
= 0,
![]() ,
,
![]() .
.
Первый интеграл
![]()
Второй интеграл
![]()
Напишем полученные
уравнения для t = 0:
![]() ,
,
![]() ,
откуда
,
откуда
![]() .
.
Уравнение угловой скорости звена 1 имеет вид
![]() (12)
(12)
Искомое уравнение вращательного движения колеса 2 имеет вид:
![]() (13)
(13)
Натяжение нити T найдем, как было показано, из уравнения (3):
![]() или
или
![]() (14)
(14)
При t = 2 с, учитывая (11) и исходные данные, имеем
![]() (15)
(15)
Окружное усилие определяем из уравнения (1):
![]() ,
при t = 2 с, учитывая (11),
имеем
,
при t = 2 с, учитывая (11),
имеем
![]()
