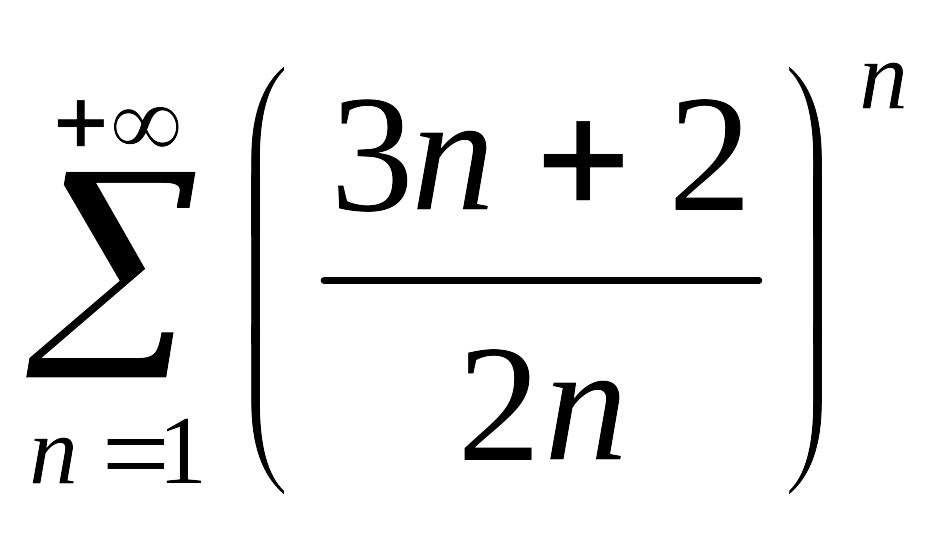Материалы по контролю и оценке учебных достижений обучающихся
«Математика 3»
для студентов 1 курса машиностроительного факультета
специальности 5В070800-«Нефтегазовое дело»
форма обучения очная
на 3 семестр 2012-2013 учебного года
Принципы и система оценки
Изучение дисциплины осуществляется в виде проведения лекций, практических или лабораторных занятий в объеме часов, предусмотренных по данной дисциплине, с проведением текущего, рубежного контроля (7 и 14 недели), итогового контроля (экзамен). Кредиты по дисциплине засчитываются, если по итогам обучения получена положительная оценка.
Положительная оценка ставится в том случае, когда студент знает весь программный учебный материал в полном объеме, выполнил все предложенные ему индивидуальные, самостоятельные и практические работы, имеет все конспекты лекций. На вопросы в пределах программы дает правильные, сознательные и уверенные ответы. В различных практических заданиях умеет самостоятельно пользоваться полученными знаниями. В устных ответах пользуется литературным, профессионально-правильным языком и не допускает ошибок.
Программой дисциплины определяются различные виды текущего контроля успеваемости обучающихся: устный опрос, письменный контроль, комбинированный контроль, презентация домашних заданий, дискуссии, тренинги, круглые столы, кейс-стади, тесты и др.
Структура оценки деятельности обучающегося
В качестве инструментов измерения знаний обучающихся выступает шкала оценок. Шкала оценок основана на балльно-рейтинговой буквенной системе.
Балльно-рейтинговая буквенная система построена по одиннадцати бальной шкале, включающей оценки по буквенной системе, соответствующий им цифровой эквивалент баллов, процентное содержание оценки и традиционные оценки. Оценками буквенной системы являются буквы алфавита английского языка от А (наивысшая оценка) до Ғ (наихудшая оценка) в зависимости от уровня знаний.
Цифровым эквивалентом баллов являются арабские цифры в десятичной системе исчисления от 4,0 до 1,0 положительные оценки и 0 - неудовлетворительная оценка.
Процентное содержание оценки определяется в процентах. При этом положительная оценка включает оценки от 50% до 100%, неудовлетворительная оценка - от 0 до 49%.
Традиционная шкала оценок строится по четырехбалльной шкале с оценками «отлично», «хорошо», «удовлетворительно», «не удовлетворительно».
Балльно-рейтинговая буквенная система применяется для оценки знаний обучающихся всех форм обучения.
Шкала оценок по балльно-рейтинговой системе
Оценка по буквенной системе |
балл |
%-ое содержание |
значение |
А |
4,00 |
95-100 |
Отлично |
А- |
3,67 |
90-94 |
|
В+ |
3,33 |
85-89 |
Хорошо |
В |
3,0 |
80-84 |
|
В- |
2,67 |
75-79 |
|
С+ |
2,33 |
70-74 |
Удовлетворительно |
С |
2,0 |
65-69 |
|
С- |
1.67 |
60-64 |
|
D+ |
1.33 |
55-59 |
|
D |
1.0 |
50-54 |
|
F |
0 |
0-49 |
Неудовлетворительно |
Экзамены преследуют цель оценить полученные студентом за курс (семестр), полученные теоретические знания, прочность их усвоения, развитие творческого мышления, приобретение навыков самостоятельной работы, умение синтезировать полученные знания и применять их для решения практических задач.
Оценка рейтинга допуска составляет 60% итоговой оценки знаний по дисциплине.
Оценка итогового контроля составляет 40% итоговой оценки знаний по дисциплине.
При явке на экзамен обучающийся обязан иметь при себе зачетную книжку со штампом о допуске к экзаменационной сессии. Присутствие на экзаменах посторонних лиц без разрешения декана факультета не допускается.
Студент, не набравший 30% рейтинга допуска в течение семестра, не допускается к экзаменам.
Студенты, обучающиеся на платной основе, не допускаются к сессии при наличии задолженности по оплате за обучение.
Студент может быть допущен к экзаменационной сессии при отсутствии зачета по курсовой работе только на первый экзамена.
Для студентов, которые не смогли сдать экзамены в общеустановленные сроки по болезни или другим уважительным причинам (семейные обстоятельства, длительные служебные командировки, стихийные бедствия), документально подтвержденным соответствующей организацией, устанавливаются индивидуальные сроки их сдачи.
Перечень вопросов и заданий рубежного контроля №1
№ |
Уровень сложности |
Вопросы |
|
|
1 |
Что называется числовым рядом? |
|
|
1 |
Что такое частичная сумма ряда
|
|
|
1 |
Числовой ряд называется сходящимся если … |
|
|
1 |
Числовой ряд называется расходящимся, если |
|
|
1 |
Необходимое условие сходимости числового ряда. |
|
|
2 |
Формула Тейлора |
|
|
1 |
Разложите
|
|
|
1 |
Разложите sinx в степенной ряд. |
|
|
1 |
Разложите в степенной ряд
|
|
|
1 |
Гармонический ряд |
|
|
2 |
Найти радиус сходимости степного ряда
|
|
|
2 |
Среди рядов:
|
|
|
2 |
Для исследования сходимости ряда
|
|
|
2 |
Найти радиус сходимости степенного
ряда
|
|
|
2 |
Среди рядов:
|
|
|
2 |
Среди рядов:
|
|
|
2 |
Для исследования, сходимости ряда
|
|
|
1 |
Радиус сходимости степенного ряда
|
|
|
1 |
Дивергенция векторного поля
|
|
|
1 |
Общий член числового ряда
|
|
|
2 |
Необходимое условие сходимости выполнено для ряда: |
|
|
1 |
Первые три члена ряда
|
|
|
1 |
Общий член числового ряда
|
|
|
2 |
Исследовать на сходимость по признаку
Даламбера
|
|
|
2 |
Исследовать на сходимость по признаку
Даламбера
|
|
|
2 |
Исследовать на сходимость по признаку
Даламбера
|
|
|
2 |
Исследовать на сходимость по признаку
Даламбера
|
|
|
2 |
Исследовать на сходимость по признаку
Даламбера
|
|
|
2 |
Исследовать на сходимость по признаку
Даламбера
|
|
|
2 |
Исследовать на сходимость по признаку
Даламбера
|
|
|
2 |
Исследовать на сходимость по признаку
Даламбера
|
|
|
2 |
Исследовать на сходимость по признаку
Даламбера
|
|
|
2 |
Исследовать на сходимость по признаку
Даламбера |
|
|
2 |
Исследовать на сходимость по признаку
Даламбера |
|
|
2 |
Исследовать на сходимость по признаку
Даламбера |
|
|
2 |
Исследовать на сходимость по признаку
Даламбера |
|
|
2 |
Исследовать на сходимость по признаку
Даламбера |
|
|
1 |
Исследовать на сходимость по признаку
Даламбера |
|
|
2 |
Исследовать на сходимость по признаку
Даламбера |
|
|
1 |
Вычислить первые пять членов ряда
|
|
|
1 |
Вычислить первые пять членов ряда
|
|
|
1 |
Вычислить первые пять членов ряда
|
|
|
1 |
Вычислить первые пять членов ряда
|
|
|
1 |
Исследовать на сходимость по
интегральному признаку Коши
|
|
|
2 |
Исследовать на сходимость по
интегральному признаку Коши
|
|
|
1 |
Исследовать на сходимость по признаку
сравнения
|
|
|
1 |
Исследовать на сходимость по признаку
сравнения
|
|
|
1 |
Исследовать на сходимость по радикальному
признаку Коши
|
|
|
2 |
Исследовать на сходимость по радикальному
признаку Коши
|
|
|
2 |
Исследовать на сходимость по радикальному
признаку Коши
|
|
|
2 |
Исследовать на сходимость по радикальному
признаку Коши
|
|
|
1 |
Исследовать на сходимость знакопеременный
ряд по признаку Лейбница
|
|
|
1 |
Исследовать на сходимость знакопеременный ряд по признаку Лейбница
|
|
|
1 |
Исследовать на сходимость знакопеременный ряд по признаку Лейбница
|
|
|
1 |
Исследовать на сходимость знакопеременный ряд по признаку Лейбница
|
|
|
1 |
Исследовать на сходимость знакопеременный ряд по признаку Лейбница
|
|
|
1 |
Исследовать на сходимость знакопеременный ряд по признаку Лейбница
|
|
|
1 |
Исследовать на сходимость знакопеременный ряд по признаку Лейбница
|
|
|
1 |
Исследовать на сходимость знакопеременный ряд по признаку Лейбница
|
|
|
1 |
Исследовать на сходимость знакопеременный ряд по признаку Лейбница
|
|
|
1 |
Исследовать на сходимость знакопеременный ряд по признаку Лейбница
|
|
|
1 |
Исследовать на сходимость знакопеременный ряд по признаку Лейбница
|
|
|
2 |
Исследовать на сходимость знакопеременный ряд по признаку Лейбница
|
|
|
1 |
Исследовать на сходимость знакопеременный ряд по признаку Лейбница
|
|
|
2 |
Исследовать на сходимость знакопеременный ряд по признаку Лейбница
|
|
|
2 |
Определить интервал сходимости
|
|
|
2 |
Определить интервал сходимости
|
|
|
2 |
Определить интервал сходимости
|
|
|
2 |
Определить интервал сходимости
|
|
|
2 |
Определить интервал сходимости
|
|
|
2 |
Определить интервал сходимости
|
|
|
2 |
Определить интервал сходимости
|
|
|
2 |
Определить интервал сходимости
|
|
|
2 |
Определить интервал сходимости
|
|
|
2 |
Определить интервал сходимости
|
|
|
2 |
Определить интервал сходимости
|
|
|
2 |
Определить интервал сходимости
|
|
|
2 |
Определить интервал сходимости
|
|
|
2 |
Формулы Фурье для составления ряда Фурье по тригонометрической системе |
|
|
1 |
Для функции
|
|
|
1 |
Для функции
написать формулу вычисления коэффициента
|
|
|
3 |
Найти коэффициент разложения
|
|
|
2 |
Найти коэффициент разложения ряда Фурье для функции на интервале |
|
|
2 |
Найти коэффициент разложения ряда Фурье для функции на интервале |
|
|
2 |
Найти коэффициент разложения
ряда Фурье для функции
|
|
|
3 |
Найти коэффициент разложения
|
|
|
2 |
Для функции
написать формулу вычисления коэффициента
ряда Фурье на интервале
|
|
|
1 |
Для функции написать формулу вычисления коэффициента ряда Фурье на интервале при разложении по синусам. |
|
|
1 |
Для функции
написать формулу вычисления коэффициента
|
|
|
1 |
Для функции написать формулу вычисления коэффициента ряда Фурье на интервале при разложении по синусам.
|
|
|
1 |
Для функции
написать формулу вычисления коэффициента
|
Перечень вопросов и заданий рубежного контроля №2
№ |
Уровень сложности |
Вопросы |
|
|
1 |
Под событием понимают такой результат эксперимента или наблюдения, который при реализации данного комплекса условий может: |
|
|
1 |
Какое событие называют достоверным? |
|
|
1 |
Какое событие называют невозможным? |
|
|
1 |
Какое событие называют случайным? |
|
|
1 |
События А и В называются несовместными, если: |
|
|
1 |
События А и В называются совместными, если при испытании: |
|
|
1 |
Перестановками называются комбинации, состоящие из: |
|
|
1 |
Размещениями называются комбинации, состоящие из: |
|
|
1 |
Сочетаниями называются комбинации, состоящие из: |
|
|
1 |
Противоположными называются: |
|
|
2 |
Условной вероятностью
|
|
|
1 |
События А и В называются независимыми, если: |
|
|
1 |
События А и В называются зависимыми, если: |
|
|
2 |
Вероятность появления хотя бы одного из событий А1, А2,…, Аn независимых в совокупности, P(A) =: |
|
|
1 |
Полная вероятность вычисляется по формуле Р(А)=: |
|
|
1 |
Укажите формулу классического определения вероятности |
|
|
1 |
Укажите формулу по которой вычисляется относительная частота |
|
|
1 |
Вероятностью события называется отношение m/n, где: |
|
|
1 |
Вероятность достоверного события равна: |
|
|
1 |
Вероятность невозможного события равна: |
|
|
1 |
Вероятность случайного события Р(А) удовлетворяет неравенствам…: |
|
|
1 |
Найдите формулу с помощью которой находятся перестановки из n различных элементов: |
|
|
1 |
Найдите формулу с помощью которой находится число размещений из n элементов по k элементов : |
|
|
1 |
Найдите формулу с помощью которой находится число сочетаний из n элементов по k элементов : |
|
|
1 |
Число всех перестановок трех элементов равно: |
|
|
1 |
Число всех перестановок четырех элементов равно: |
|
|
1 |
Число всех перестановок пяти элементов равно: |
|
|
1 |
Сколько трехзначных чисел можно составить из чисел 1,2,3, если каждая цифра входит в изображение числа только один раз? |
|
|
1 |
Число всех размещений пяти элементов по два равно: |
|
|
1 |
Число всех размещений шести элементов по три равно: |
|
|
1 |
Число всех размещений шести элементов по пять равно: |
|
|
1 |
Сколько трехзначных чисел можно составить из чисел 1,2,3,4,5 без повторений? |
|
|
1 |
Сколько можно составить сигналов из 6 флажков различного цвета, взятых по 2? |
|
|
1 |
Число всех сочетаний из семи элементов по три равно: |
|
|
1 |
Число всех сочетаний из ста элементов по девяносто восемь равно: |
|
|
1 |
Сколькими способами можно составить букет из 3-х роз, если в вазе их 6. |
|
|
1 |
Сколькими способами можно выбрать 2 детали из ящика, содержащего 10деталей. |
|
|
1 |
Набирая номер телефона, абонент забыл одну цифру и набрал ее наудачу. Найти вероятность того, что набрана нужная цифра. |
|
|
1 |
Брошена игральная кость. Найти вероятность того, что выпадет четное число очков. |
|
|
1 |
Игральная кость подбрасывается один раз. Найти вероятность того, что выпадет число очков равное шести. |
|
|
1 |
Игральная кость подбрасывается один раз. Найти вероятность того, что выпадет число очков кратное трем. |
|
|
1 |
Игральная кость подбрасывается один раз. Найти вероятность того, что выпадет число очков меньше пяти. |
|
|
1 |
Игральная кость подбрасывается один раз. Найти вероятность того, что выпадет число очков больше двух. |
|
|
1 |
Подбрасываются две игральные кости. Найти вероятность того, что число очков на игральных костях совпадает. |
|
|
1 |
Подбрасываются две игральные кости. Найти вероятность того, что число очков на первой кости больше, чем на второй. |
|
|
1 |
Подбрасываются две игральные кости. Найти вероятность того, что сумма очков четна. |
|
|
1 |
Подбрасываются две игральные кости. Найти вероятность того, что сумма очков больше двух. |
|
|
1 |
Подбрасываются две игральные кости. Найти вероятность того, что сумма очков не меньше пяти. |
|
|
1 |
Подбрасываются две игральные кости. Найти вероятность того, что хотя бы на одной кости появится цифра шесть. |
|
|
1 |
Подбрасываются две игральные кости. Найти вероятность того, что произведение очков равно шести. |
|
|
1 |
Подбрасываются две игральные кости. Найти вероятность того, что сумма выпавших очков равна семи. |
|
|
1 |
Подбрасываются две игральные кости. Найти вероятность того, что сумма выпавших очков равна восьми, а разность - четырем. |
|
|
1 |
Подбрасываются две игральные кости. Найти вероятность того, что сумма выпавших очков равна пяти, а произведение - четырем. |
|
|
1 |
В партии из 100 деталей отдел технического контроля обнаружил 5 нестандартных деталей. Чему равна относительная частота появления нестандартных деталей? |
|
|
1 |
По цели произвели 35 выстрелов. Было зафиксировано 21 попаданий. Чему равна относительная частота поражения цели? |
|
|
1 |
По цели произведено 20 выстрелов, причем зарегистрировано 18 попаданий. Найти относительную частоту попадания в цель. |
|
|
1 |
При испытании партии приборов относительная частота годных приборов оказалась равной 0,9. Найти число годных приборов, если всего было произведено 200 приборов. |
|
|
2 |
Известно, что всхожесть семян пшеницы 90 %. Сколько необходимо взять зерен, чтобы взошло 360 растений. |
|
|
2 |
При стрельбе из винтовки относительная частота попадания в цель оказалась равной 0,85. Найти число попаданий, если всего было произведено 120 выстрелов. |
|
|
2 |
Всхожесть семян пшеницы 90 %. Сколько необходимо взять зерен, чтобы взошло 200 растений. |
|
|
1 |
В урне 20 шаров с номерами от 1 до 20. Какова вероятность вынуть из урны шар с номером 37? |
|
|
1 |
Игральная кость будет брошена 2 раза. Какова вероятность того, что сумма выпавших очков при этом будет не меньше 10? |
|
|
1 |
В урне 12 шаров: 3 белых, 4 черных, 5 красных. Какова вероятность вынуть из урны черный шар? |
|
|
1 |
Участники жеребьевки тянут из ящика жетоны с номерами от 1 до 100. Найти вероятность того, что номер первого наудачу извлеченного жетона не содержит цифры 5? |
|
|
1 |
В мешочке имеется 5 одинаковых кубиков. На всех гранях каждого кубика написана одна из следующих букв: о, п, р, с, т. Найти вероятность того, что на вынутых по одному и расположенных в одну линию кубиков можно будет прочесть слово «спорт» |
|
|
1 |
На карточках написаны буквы У, А, З, К, Т. Карточки перемешиваются и раскладываются в ряд. Какова вероятность того, что получится слово ЗКАТУ: |
|
|
1 |
В урне 15шаров: 5 белых и 10 чёрных. Какова вероятность вынуть из урны белый шар? |
|
|
1 |
Бросают 2 игральные кости. Подсчитать вероятность выпадения 7 очков. |
|
|
1 |
Из слова «студент» случайным порядком выбирают букву. Какова вероятность, что выбранной окажется гласная буква: |
|
|
1 |
Найти вероятность того, что наудачу
выбранное из отрезка
|
|
|
1 |
Найти вероятность того, что при бросании игральной кости выпадет число, делящееся на 3: |
|
|
1 |
Найти вероятность того, что при подбрасывании двух монет хотя бы на одной из них выпадет герб: |
|
|
1 |
Найти вероятность того, что карта вынутая из колоды в 36 карт, окажется тузом: |
|
|
1 |
В урне 15 шаров : 5 белых и 10 черных. Какова вероятность вынуть из урны синий шар: |
|
|
1 |
В урне 10 шаров : 3 белых и 7 черных. Из урны наугад вынимается один шар. Какова вероятность того, что этот шар белый? |
|
|
1 |
В урне 10 шаров : 3 белых и 7 черных. Из урны наугад вынимается один шар. Какова вероятность того, что этот шар черный? |
|
|
1 |
Из слова «наугад» выбирается одна буква. Какова вероятность того, что эта буква «я»? |
|
|
1 |
Из слова «наугад» выбирается одна буква. Какова вероятность того, что это гласная буква ? |
|
|
2 |
Брошены три монеты. Найти вероятность того, что выпадут два «герба» |
|
|
2 |
Брошены две игральные кости. Какова вероятность выпадения на двух костях в сумме не менее 9 очков? |
|
|
2 |
Брошены две игральные кости. Какова вероятность выпадения единицы, по крайней мере на одной кости? |
|
|
2 |
Из пяти карточек с буквами А, Б, В, Г, Д наугад одна за другой выбираются три и располагаются в ряд в порядке появления. Какова вероятность того, что получится слово «ДВА»? |
|
|
2 |
Ребенок играет с четырьмя буквами разрезной азбуки А, А, М, М. Какова вероятность того, что при случайном расположении букв в ряд он получит слово «МАМА»? |
|
|
2 |
Точка взята наудачу внутри круга радиуса R. Найти вероятность того, что эта точка окажется от центра на расстоянии, меньшем r (rR). |
|
|
2 |
На отрезке длины 20 см помещен меньший отрезокдлины 10 см. Найти вероятность того, что точка наудачу поставленная на больший отрезок, попадет также и на меньший отрезок. предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения. |
|
|
3 |
Внутрь круга радиуса R наудачу брошена точка. Найти вероятность того, что точка окажется внутри вписанного в круг правильного шестиугольника. Предполагается, что вероятность попадания точки в часть круга пропорциональна площади этой части и не зависит от ее расположения относительно круга. |
|
|
3 |
Внутрь круга радиуса R наудачу брошена точка. Найти вероятность того, что точка окажется внутри вписанного в круг правильного треугольника. Предполагается, что вероятность попадания точки в часть круга пропорциональна площади этой части и не зависит от ее расположения относительно круга. |
|
|
3 |
Внутрь круга радиуса R наудачу брошена точка. Найти вероятность того, что точка окажется внутри вписанного в круг квадрата. Предполагается, что вероятность попадания точки в часть круга пропорциональна площади этой части и не зависит от ее расположения относительно круга. |
|
|
2 |
Талоны занумерованы всеми двузначными числами. Из пачки наудачу берут 1 талон. Найти вероятность того, что номер талона состоит из одинаковых цифр. |
|
|
2 |
Найти вероятность выигрыша наибольшей суммы при игре в лото 5 из 36 |
|
|
1 |
Пусть в результате испытания ожидаются события А и В. Сумма этих событий, А+В, означает: |
|
|
2 |
Пусть в результате испытания ожидаются события А и В. Произведение этих событий, АВ, означает: |
|
|
1 |
Если события А и В несовместны, то p(A+B)=: |
|
|
2 |
Если события А и В независимы, то p(AB)=: |
|
|
2 |
Формула вероятности противоположного события: |
|
|
2 |
Формула Бейеса |
|
|
2 |
Локальная теорема Лапласа вычисляется Pn(k)=: |
|
|
2 |
Интегральная теорема Лапласа вычисляется Pn(k1, k2)=: |
|
|
1 |
Вероятность того, что день будет ясным р=0,7. Найти вероятность того, что день будет дождливым: |
|
|
2 |
Предстоит опыт: из колоды 36 карт будет вынута одна. Какова вероятность того, что эта карта - туз или король? |
|
|
2 |
В ящике 4 белых, 5 красных, 8 зеленых и 3 голубых шара. Шары перемешивают и извлекают один шар. Какова вероятность события, состоящего в том, что шар окажется цветным? |
|
|
3 |
В цехе работают 2 транспортера. Вероятность безотказной работы за время t каждого из них равна 0,9. Транспортеры работают независимо друг от друга. Найти вероятность того, что за время t будут работать хотя бы один транспортер. |
|
|
3 |
В цехе работают 2 транспортера. Вероятность безотказной работы за время t каждого из них равна 0,9. Транспортеры работают независимо друг от друга. Найти вероятность того, что за время t будут работать оба транспортера. |
|
|
3 |
В цехе работают 2 транспортера. Вероятность безотказной работы за время t каждого из них равна 0,9. Транспортеры работают независимо друг от друга. Найти вероятность того, что за время t не будет работать ни один транспортер. |
|
|
3 |
В цехе работают 2 транспортера. Вероятность безотказной работы за время t каждого из них равна 0,9. Транспортеры работают независимо друг от друга. Найти вероятность того, что за время t будет работать только один транспортер. |
|
|
3 |
Устройство состоит из трех элементов, работающих независимо. Вероятность безотказной работы за время t первого, второго и третьего элементов соответственно равны 0,6; 0,7; 0,8. Найти вероятности того, что за время t безотказно будут работать только один элемент. |
|
|
3 |
Устройство состоит из трех элементов, работающих независимо. Вероятность безотказной работы за время t первого, второго и третьего элементов соответственно равны 0,6; 0,7; 0,8. Найти вероятности того, что за время t безотказно будут работать только два элемент. |
|
|
3 |
Устройство состоит из трех элементов, работающих независимо. Вероятность безотказной работы за время t первого, второго и третьего элементов соответственно равны 0,6; 0,7; 0,8. Найти вероятности того, что за время t безотказно будут работать все три элемента. |
|
|
3 |
Три стрелка стреляют по мишени. Вероятность попадания в цель первым стрелком равна 0,6; вторым - 0,7; третьим – 0,8. Найти вероятность того, что при одном выстреле в цель попадет только один из стрелков. |
|
|
3 |
Три стрелка стреляют по мишени. Вероятность попадания в цель первым стрелком равна 0,6; вторым - 0,7; третьим – 0,8. Найти вероятность того, что при одном выстреле в цель попадут все три стрелка. |
|
|
3 |
Три стрелка стреляют по мишени. Вероятность попадания в цель первым стрелком равна 0,6; вторым - 0,7; третьим – 0,8. Найти вероятность того, что при одном выстреле в цель попадет хотя бы один из стрелков. |
|
|
3 |
Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сигнализатор сработает, равна 0,95 для первого сигнализатора и 0,9 для второго. Найти вероятность того, что при аварии сработает только один сигнализатор. |
|
|
3 |
Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сигнализатор сработает, равна 0,95 для первого сигнализатора и 0,9 для второго. Найти вероятность того, что при аварии сработает оба сигнализатора. |
|
|
3 |
Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сигнализатор сработает, равна 0,95 для первого сигнализатора и 0,9 для второго. Найти вероятность того, что при аварии сработает хотя бы один сигнализатор. |
|
|
2 |
Вероятность попадания в цель р=0,9. Определить вероятность того, что при 3 выстрелах будет 3 попадания. |
|
|
2 |
В первом ящике деталей первого сорта 30%, во втором 40%. Вынимаются по одной детали из каждого ящика. Определить вероятность того, что обе вынутые детали первого сорта. |
|
|
3 |
Вероятность того, что стрелок при одном выстреле выбьет 10 очков, равна 0,1; вероятность выбить 9 очков равна 0,3; вероятность выбить 8 или меньше очков равна 0,6. Найти вероятность того, что при одном выстреле стрелок выбьет не менее 9 очков. |
|
|
2 |
Посажены два саженца с вероятностями выживания равными 0.7 и 0.6 . Какова вероятность того, что один из них погибнет? |
|
|
2 |
Два стрелка с вероятностями попадания в цель, равными 0.9 и 0.8, будут делать по одному выстрелу по мишени. Какова вероятность двух попаданий? |
|
|
3 |
Дорогое электрическое оборудование снабжено тремя предохранителями, соединенными последовательно. Вероятности их надежности при единичной аварийной ситуации равны 0.9, 0.8 и 0.7. Какова вероятность того, что при такой ситуации сработает хотя бы один предохранитель? |
|
|
3 |
Три стрелка независимо друг от друга стреляют по цели. Вероятность попадания в цель для первого стрелка равна 0,75, для второго 0,8, для третьего 0,9. Определить вероятность того, что все три стрелка одновременно попадут в цель: |
|
|
3 |
Три стрелка независимо друг от друга стреляют по цели. Вероятность попадания в цель для первого стрелка равна 0,75, для второго 0,8, для третьего 0,9. Определить вероятность того, что в цель попадет хотя бы один стрелок: |
|
|
3 |
В электрическую цепь включены 3 элемента, работающие независимо один от другого. Вероятности отказов I,II,III элементов соответственно равны 0,1;0,15;0,2. Найти вероятность того, что в цепи не будет работать хотя бы один элемент: |
|
|
2 |
Найти вероятность появления 2 «гербов» при одном подбрасывании 2 монет: |
|
|
2 |
2 стрелка стреляют по очереди. Вероятность попадания в цель первого стрелка 0,9, второго – 0,8. Найти вероятность попадания хотя бы одного стрелка. |
|
|
2 |
В студии телевидения три телекамеры. Для каждой камеры вероятность того, что она включена в данный момент, равна 0,6. Найти вероятность того, что в данный момент включена хотя бы одна камера. |
|
|
2 |
Два стрелка стреляют по очереди Вероятность попадания в цель первого стрелка 0,7 , а второго 0,8. Найти вероятность попадания хотя бы одного стрелка: |
|
|
3 |
С первого станка на сборку поступает 40%, со второго – 30%, с третьего – 20%, с четвертого – 10% всех деталей. Среди деталей первого станка 0,1% бракованных, второго – 0,2%, третьего -0,25%, четвертого – 0,5%. Найти вероятность того, что поступившая на сборку деталь - бракованная. |
|
|
3 |
Для участия в студенческих отборочных соревнованиях выделено из первой группы курса 4, из второй – 6, из третьей – 5 студентов. Вероятности того, что студент 1,2,3 группы попадет сборную института, соответственно равны 0,9; 0,7; 0,8. Наудачу выбранный студент в итоге соревнования попал в сборную. Найти вероятность того, что студент попал в сборную. |
|
|
3 |
В ящике 12 деталей изготовленных на заводе №1, 20 деталей изловленных на заводе №2, 18 деталей изловленных на заводе №3. Вероятность того, что деталь изготовлена на заводе №1 отличного качества, равна 0,9; для деталей изготовленных на заводе №2,3 эти вероятности соответственно равны 0,6 и 0,9. Найти вероятность того, что извлеченная наудачу деталь окажется отличного качества. |
|
|
3 |
Вероятности того, что во время работы цифровой электронной машины произойдет сбой в арифметическом устройстве, в оперативной памяти, в остальных устройствах, относятся как 3:2:5. Вероятности обнаружения сбоя в арифметическом устройстве, в оперативной памяти, в остальных устройствах соответственно равны 0,8; 0,9; 0,9. Найти вероятность того, что возникший в машине сбой будет обнаружен. |
|
|
3 |
В пирамиде 5 винтовок, 3 из которых снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом, равна 0,95; для винтовки без оптического эта вероятность будет равна 0,7. Найти вероятность того, что мишень будет поражена, если стрелок произведет один выстрел из наудачу взятой винтовки. |
|
|
3 |
В двух ящиках находятся детали: в первом - 10 (из них 3 стандартных), во втором - 15 (из них 6 стандартных). Из каждого ящика наудачу вынимают по одной детали. Найти вероятность того, что обе детали окажутся стандартными. |
|
|
3 |
Среди 100 лотерейных билетов есть 5 выигрышных. Найти вероятность того, что 2 наудачу выбранные билета окажутся выигрышными. |
|
|
3 |
В читальном зале имеется 6 учебников по теории вероятности, из которых 3 в переплете. Библиотекарь наудачу взял два учебника. Найти вероятность того, что оба учебника окажутся в переплете. |
|
|
3 |
В цехе работают 7 мужчин и 3 женщины. По табельным номерам наудачу отобраны 3 человека. Найти вероятность того, что все отобранные лица окажутся мужчинами. |
|
|
3 |
В ящике 10 деталей, среди которых 6 окрашенных. Сборщик наудачу извлекает 4 детали. Найти вероятность того, что все излеченные детали окажутся окрашенными. |
|
|
2 |
Предстоит опыт: монета будет брошена 2 раза. Какова вероятность того, что оба раза появится «орел»? |
|
|
2 |
В корзине 10 шаров, из них 4 – красного цвета. Предстоит опыт: из корзины друг за другом, без возвращения первого обратно в корзину, будут взяты два шара. Какова вероятность того, что оба они окажутся красного цвета? |
|
|
2 |
В трех одинаковых коробках по 10 одинаковых деталей. Причем в двух коробках по 3 некондиционных детали, а в одной коробке 1 некондиционная деталь. Какова вероятность того, что взятая из случайно вскрытой коробки деталь окажется некондиционной? |
|
|
2 |
Брошены монета и игральная кость. Найти вероятность того, что выпадут «орел » и «6 очков»: |
|
|
3 |
Имеются два одинаковых ящика с шарами. В первом ящике 2 белых и 1 черный шар, во втором – 1 белый и 4 черных шара. Наудачу выбирают один ящик и вынимают из него один шар. Какова вероятность того, что вынутый шар окажется белым? |
|
|
3 |
В цехе работают 20 станков. Из них 10 марки А, 6 марки Б и 4 марки С. Вероятность того, что качество детали окажется отличным, для этих станков соответственно равна: 0,9, 0,8, 0,7. Какой процент отличных деталей выпускает цех в целом? |
|
|
3 |
Предположим, что 5% всех мужчин и 0,25% всех женщин дальтоники. Наугад выбранное лицо страдает дальтонизмом. Какова вероятность того, что это мужчина? (Считать, что мужчин и женщин одинаковое число) |
|
|
3 |
На фабрике, изготовляющей болты, первая машина производит 25% , вторая 35%, третья 40% всех изделий. В их продукции брак составляет соответственно 5%, 4% и 2%. Какова вероятность того, что случайно выбранный болт дефектный? |
|
|
3 |
На фабрике, изготовляющей болты, первая машина производит 25% , вторая 35%, третья 40% всех изделий. В их продукции брак составляет соответственно 5%, 4% и 2%. Случайно выбранный из продукции болт оказался дефектным. Какова вероятность того, что он был произведен первой машиной? |
|
|
3 |
На фабрике, изготовляющей болты, первая машина производит 25% , вторая 35%, третья 40% всех изделий. В их продукции брак составляет соответственно 5%, 4% и 2%. Случайно выбранный из продукции болт оказался дефектным. Какова вероятность того, что он был произведен второй машиной? |
|
|
3 |
На фабрике, изготовляющей болты, первая машина производит 25% , вторая 35%, третья 40% всех изделий. В их продукции брак составляет соответственно 5%, 4% и 2%. Случайно выбранный из продукции болт оказался дефектным. Какова вероятность того, что он был произведен третьей машиной? |
|
|
3 |
В продажу поступают телевизоры трех заводов. Продукция первого завода содержит 20% телевизоров со скрытым дефектом, второго 10% и третьего – 5%. Какова вероятность приобрести исправный телевизор, если в магазин поступило 30% телевизоров с первого завода, 20% со второго и 50% с третьего завода ? |
|
|
3 |
На двух станках производятся одинаковые детали. Вероятность того, что деталь стандартная, для первого станка равна 0,8, для второго 0,9. производительность второго станка втрое больше, чем первого. Найти вероятность того, что взятая наудачу деталь отличного качества окажется стандартной |
|
|
2 |
Предположим, что для одной торпеды вероятность потопить корабль равна 1/2. Какова вероятность того, что 4 торпеды потопят корабль, если для потопления корабля достаточно одного попадания торпеды в цель? |
|
|
2 |
В ящике 10 красных и 5 синих пуговиц. Вынимаются наудачу все пуговицы. Какова вероятность того, что пуговицы будут одноцветными. |
|
|
2 |
Определить вероятность того, что в семье, имеющей 5 детей будет 3 девочки и 2 мальчика. Вероятности рождения мальчика и девочки предполагаются одинаковыми. |
|
|
2 |
Всхожесть семян данного растения составляет 90%. Найти вероятность того, что из четырех посеянных семян взойдут три. |
|
|
2 |
В хлопке число длинных волокон составляет 80%. Какова вероятность того, что среди взятых наудачу 5 волокон длинных окажется три. |
|
|
2 |
В некотором водоеме карпы составляют 80%. Найти вероятность того, что из 5 выловленных в этом водоеме рыб окажется 4 карпа. |
|
|
2 |
Прибор состоит из 4 узлов. Вероятность безотказной работы в течение смены для каждого узла равна 0,8. Узлы выходят из строя независимо друг от друга. Найти вероятность того, что за смену откажут два узла. |
|
|
2 |
Монету подбрасывают 8 раз. Какова вероятность того, что 6 раз она упадет гербом вверх? |
|
|
2 |
В цехе 6 моторов. Для каждого мотора вероятность того, что он в данный момент включен, равна 0,8. Найти вероятность того, что в данный момент включен 4 мотора. |
|
|
2 |
Вероятность того, что стрелок при одном выстреле попадает в мишень, равна р=0,9. Стрелок произвел 3 выстрела. Найти вероятность того, что все 3 выстрела дали попадание. |
|
|
2 |
В цехе 6 моторов. Для каждого мотора вероятность того, что он в данный момент включен, равна 0,8. Найти вероятность того, что в данный момент включены все моторы |
|
|
2 |
В цехе 6 моторов. Для каждого мотора вероятность того, что он в данный момент включен, равна 0,8. Найти вероятность того, что в данный момент выключены все моторы: |
|
|
1 |
Формула Бернулли |
|
|
2 |
Посажены пять одинаковых саженцев яблони с вероятностями выживания, равными 0.8. Какова вероятность того, что выживут четыре из них? |
|
|
3 |
Изделия некоторого производства содержат 5 % брака. Найти вероятность того, что среди пяти взятых наугад изделий нет ни одного испорченного. |
|
|
3 |
Изделия некоторого производства содержат 5 % брака. Найти вероятность того, что среди пяти взятых наугад изделий будут два испорченных. |
|
|
3 |
Для прядения смешаны поровну белый и окрашенный хлопок. Какова вероятность того, что среди пяти случайно выбранных волокон смеси обнаружено менее двух окрашенных? |
|
|
2 |
Всхожесть семян данного сорта растений оценивается с вероятностью, равной 0,8. Какова вероятность того, что из пяти посеянных семян взойдут не менее четырех? |
|
|
3 |
Два равносильных шахматиста играют в шахматы. Что вероятнее: выиграть две партии из четырех или три партии из шести (ничьи во внимание не принимаются)? |
|
|
3 |
Найти вероятность того, что событие
А наступит ровно 70 раз в 243 испытаниях,
если вероятность появления этого
события в каждом испытании равна 0,25.
( |
|
|
3 |
Вероятность поражения мишени при одном выстреле равна 0,8. Найти вероятность того, что при 100 выстрелах мишень будет поражена ровно 75 раз ( (1,25)=0,1826) |
|
|
3 |
Вероятность рождения мальчика равна 0,51. найти вероятность того, что среди 100 новорожденных окажется 50 мальчиков ( (0,2)=0,3910) |
|
|
3 |
Магазин получил 1000 бутылок минеральной воды. Вероятность того, что при перевозке бутылка окажется разбитой равна 0,003. Найти вероятность того, что магазин получит разбитых бутылок ровно две (е-3= 0,04979) |
|
|
3 |
Учебник издан тиражом 100000 экземпляров. Вероятность того, что учебник сброшюрован неправильно равна 0,0001. Найти вероятность того, что тираж содержит ровно 5 бракованных книг (е-10= 0,000045) |
|
|
1 |
Случайная величина называется дискретной, если число принимаемых ею значений: |
|
|
1 |
Математическое ожидание постоянной величины (числа) С равно: |
|
|
1 |
Дисперсия постоянной величины (числа) С равна: |
|
|
1 |
Среднее квадратическое отклонение постоянной величины (числа) С равно: |
|
|
2 |
Задан закон распределения дискретной случайной величины Х. Найти математическое ожидание М(Х)
Р | 0,3|0,2 | 0,4| 0,1| |

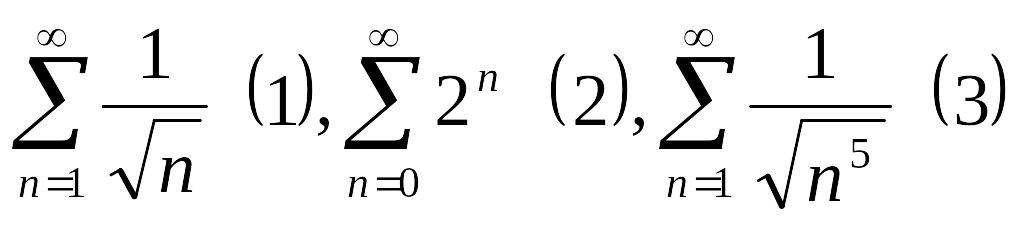 укажите расходящиеся ряды:
укажите расходящиеся ряды: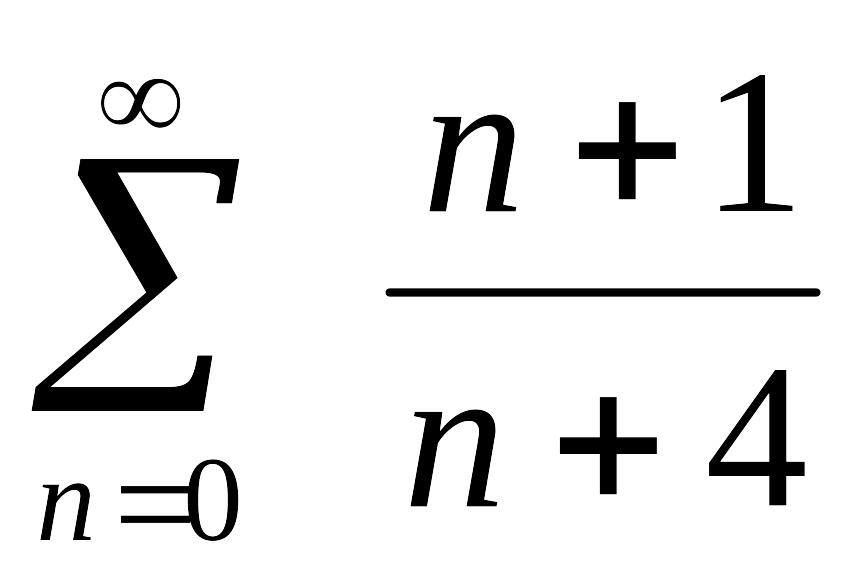 надо применить:
надо применить: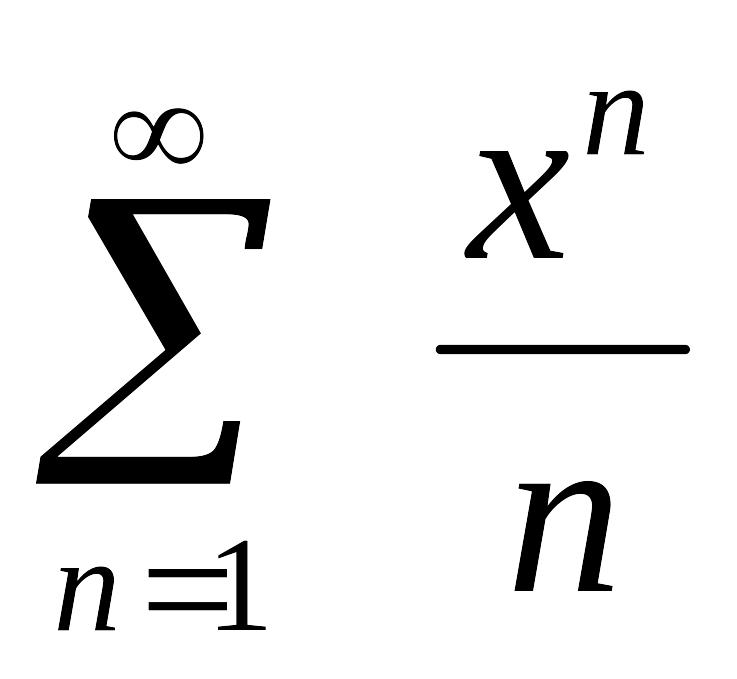 равен:
равен: