2.1.Построение ортогональной проекции точки на плоскость

Ортогональная проекция точки на плоскость строится следующим образом:

1).Из точки на плоскость опускают перпендикуляр;

2). Находят точку пересечения перпендикуляра с плоскостью. Эта точка и есть ортогональная проекция точки на плоскость.

Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости. В начертательной геометрии в качестве этих пересекающихся прямых выбирают главные линии плоскости - горизонталь и фронталь, так как по теореме о проецировании прямого угла он проецируется на плоскость проекций в натуральную величину, если одна его сторона параллельна этой плоскости.

Так как горизонталь параллельна горизонтальной плоскости проекций, на нее угол между перпендикуляром и горизонталью спроецируется в натуральную величину, и на чертеже угол между горизонтальными проекциями перпендикуляра и горизонтали будет равен 90 градусов.

Аналогично будут расположены на чертеже фронтальные проекции перпендикуляра и фронтали.

Следовательно, решение задачи начинают с проведения в плоскости параллелограмма главных линий: горизонтали и фронтали. Для примера разберем нахождение ортогональной проекции вершины А на плоскость параллелограмма (рис.12).

.

Из вершины треугольника А проводят прямую перпендикулярно плоскости параллелограмма. На чертеже это будет выглядеть так:

1). из горизонтальной проекции точки А проводят проекцию перпендикуляра перпендикулярно горизонтальной проекции горизонтали;

2).из фронтальной проекции точки А проводят проекцию перпендикуляра перпендикулярно

фронтальной проекции фронтали.

После построения перпендикуляра приступают к нахождению точки пересечения перпендикуляра с плоскостью параллелограмма. Эта задача подробно разобрана в задаче №1,как задача по определению точки пересечения прямой с плоскостью.

В результате получают ортогональную проекцию точки А на плоскость параллелограмма.

Повторяя предыдущее решение для вершин В и С, находят ортогональные проекции этих точек на плоскость параллелограмма. Последовательно соединяя ортогональные проекции точек, получают ортогональную проекцию треугольника на плоскость параллелограмма.

2.2.Пример решения задачи

Пусть Вас не пугает нагромождение линий. Все эти построения можно провести на отдельных чертежах поочередно для всех трех вершин, а затем их можно объединить в один чертеж. Для проверки решения можно сравнить его с первой задачей. Линия пересечения плоскостей треугольника и параллелограмма, построенная в первой задаче, должна совпасть с линией, соединяющей точки пересечения сторон треугольника ABC и его ортогональной проекции.

3.Задача№3.

Дана плоскость треугольника АВС. Построить падающие тени треугольника на плоскости проекций.

Решение этой задачи проводится с помощью определения падающих теней точек (вершин треугольника) на плоскости проекций.

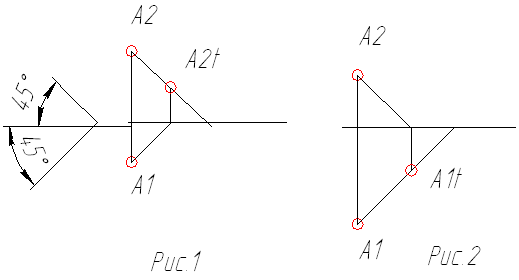
Для построения падающих теней определим, что солнечные лучи проецируются на плоскости проекций под углом 45 градусов. Эти лучи показаны на рисунке 1.

Для построения тени от точки через точку проводят солнечный луч и определяют точку пересечения луча с плоскостью проекций. На чертеже это выглядит так: через проекции точки проводят проекции луча, затем определяют точку пересечения луча с плоскостью проекций.

Эта точка есть след луча.

Луч может пересечь горизонтальную плоскость проекций, тогда он имеет горизонтальный след, т.е. тень от точки падает на горизонтальную плоскость. Для нахождения горизонтального следа на чертеже надо продолжить фронтальную проекцию луча до пересечения с осью X, из полученной точки провести перпендикуляр до пересечения с горизонтальной проекцией луча. Эта точка и есть тень заданной точки на горизонтальную плоскость проекций (рис.2).

Для нахождения фронтального следа луча на чертеже надо продолжить горизонтальную проекцию луча до пересечения с осью X, из полученной точки провести перпендикуляр до пересечения с фронтальной проекцией луча. Эта точка и есть тень заданной точки на фронтальную плоскость проекций (рис.1).

На рисунке 3 показан пример решения задачи. Точки А и В дают тень на горизонтальную плоскость проекций А_т1 и В_т1. Точка С дает тень на фронтальную плоскость проекций С_т2.

Отсюда следует, что часть тени треугольника АВС падает на плоскость горизонтальную, а часть – на фронтальную плоскость проекций. Для определения преломления тени строят тень от точки С на горизонтальную плоскость С_т1. Эта точка является мнимой, но она нужна для определения места преломления. После определения тени С_т1 соединяют горизонтальные тени А_т1В_т1С_т1.Точки пересечения этого треугольника с осью X дают точки преломления падающей тени треугольника.