Связь между параметрами процесса.
Если индикаторная диаграмма обработана, то
pvn = const или p1v1n = p2v2n и p1/p2 = (v2/v1)n (3.7)
для любых двух состояний процесса. Для рабочих тел, у которых уравнения состояния или сложны или, чаще, просто отсутствуют, найти связь температуры Т с другими параметрами состояния р или v аналитическим путем невозможно.
Для идеального газа, т.е. кроме связи pvn = const еще справедлива связь pv = RуT, сочетание этих зависимостей позволяет получить взаимосвязь:
T1 / T2 = (v2 / v1)n-1 = (p1 / p2)(n-1)/n . (3.8)
Замечание. Вывод связей (3.8) предлагаем провести самостоятельно.
Частные политропные процессы.
Если какой-то параметр состояния при взаимодействии с внешней средой фиксировать, то процесс, входящий в гамму политропных, называют частным:
pvn = const и p = const → n = 0 – изобарный,
а для идеального газа из (3.8) T1/T2 = v1/v2.
pvn = const и v = const → n = ± ∞ - изохорный,
а для идеального газа из (3.8) T1/T2 = p1/p2.
pvn = const и T = const – изотермический,
а для идеального газа n = 1 и из (3.8) v2/v1 = p1/p2.
При s = const → n = k ≡ cp / cv – изоэнтропийный (адиабатный) с уравнением
pvk = const.
Замечание. Условие Q (q) = 0 (нет источников теплоты) означает, что Tds ≡ 0 и s = const и по первому признаку процесс назван адиабатным (adiabatos – непереходимая – в смысле тепловой изоляции)
На рис.3.2 представлены графики политроп с различными показателями n для частных процессов, только еще раз напомним, что величина показателя адиабаты для двухатомных газов k ≈ 1,4.
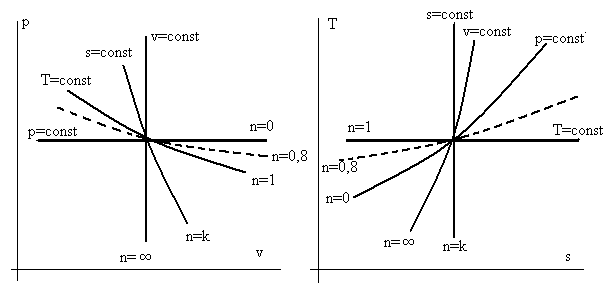
Рис. 3.2. Взаимное расположение частных политропных
процессов в осях p – v и T – s при различных значениях
показателей политропы n.
Замечание. Если необходимо построить график оригинального политропного процесса, т.е. не совпадающего с указанными частными, то, зная величину n , не сложно построить этот график на фоне частных процессов.
Пример. Построить график политропного процесса с показателем политропы n = 0,8 в осях p – v и T – s.
Решение этой задачи основано на том обстоятельстве, что линии частных процессов делят всю плоскость с координатными осями на сектора. Следовательно, график (в осях p – v или T – s) политропного процесса с каким-то n должен проходить в соответствующем секторе. На рис. 3.2 линия с n = 0,8 расположена в секторе между политропами n = 0 и n = 1 и обозначена пунктиром.
Расчет изменения функций состояния Δu, Δh и количеств воздействия (функций процесса q, w).
1.3.1. Рабочее тело - идеальный газ.
В лекции 2 представлены все способы, расчетные формулы для определения изменения функций состояния и функций процесса при любом n для любого вещества. Исключение среди них составляет процесс с n = 1, т.е. изотермический процесс. Действительно, раcчетная формула для работы деформации
w = Rу(T1 – T2) / (n – 1) и n → 1, т.е. T1 → T2,
демонстрирует неопределенность типа 0 / 0. Здесь поступаем следующим образом. Для процесса T = const и идеального газа имеем
Δu = cv|t1t2(t2 – t1) и при t2 = t1
0 = Δu = q – w → q = w = ∫pdv
и pv = RуT → p = RуT / v; подставим эту зависимость в интеграл для работы:
q = w = ∫RуT / v dv = RуT ln v2/v1 Дж/кг (3.9)
Соответственно, q = TΔs → Δs =q / T = Rу ln v2 / v1 Дж/кгК (3.10)
Таким образом, рассчитывается не абсолютное значение энтропии, а ее условное значение от s0 = 0 при избираемом удобном состоянии вещества. В инженерной практике для газов это – р = 1 бар (или 1 ата) и Т = 273К.
Замечание. Глядя на расчетные формулы (3.5) и (3.6) для истинной и средней политропной теплоемкости, видно, что при n → 1 обе теплоемкости стремятся к ±∞. Это и понятно из самого определения истинной и средней теплоемкости: делить на 0 математика не разрешает. Но это совсем не мешает рассчитать количество теплоты и изменение энтропии термодинамически, без использования калориметрии, т.е. без применения понятия теплоемкости.
Ссылка. В методических указаниях по дисциплине «Техническая термодинамика» для самостоятельной работы студентов, разработанных проф. П. Г. Алексеевым в 2003 году, МИТХТ, на стр. 16 представлена таблица 5.1, в которой приводятся в концентрированном виде все соотношения и расчетные формулы для расчета процессов при любом значении n для идеального газа.