Расчет количества теплоты и энтропия.
Из лекции 1 и анализа определения теплоемкости понятно, что количество теплоты можно определить двояко – через теплоемкости и через энтропию. Действительно, dq = cdT или dq = Tds, т.е. cdT = Tds, а переходя на геометрическую интерпретацию определенного интеграла ∫dq, как площади под кривой, можно воспользоваться тепловыми диаграммами с координатами с – Т или Т – s (см. рис. 2.6.).
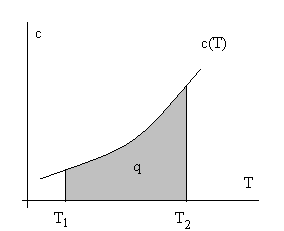
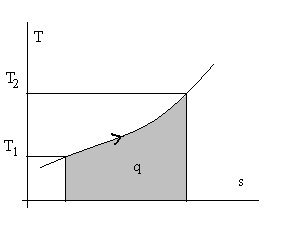
Рис.2.6. Тепловые диаграммы с – Т и Т – s для некоторого вещества.
Заштрихована площадь, численно равная количеству теплоты.
Разумеется, вторая, т.е. Т – s диаграмма, более содержательна и строга, т.к. она имеет координаты в виде функций состояния. Остается для интегрирования выразить T через s (или сх через Т), что возможно при известных свойствах веществ.
3. Термодинамические свойства веществ.
3.1. Свойства веществ и расчет внутренней энергии и энтальпии.
Ранее мы получили важный результат: внутренняя энергия u(s,v) является функцией координат состояния s и v. С другой стороны имеем уравнение состояния рабочего тела, предоставленное физиками, T = T(s,v). Из этого уравнения ничто не мешает найти энтропию s = s(T,v) и подставить ее в зависимость для u(s,v). Получим новую зависимость u(s(T,v),v) = u(T,v) и для последней распишем полный дифференциал внутренней энергии du:
du = (∂u/∂T)vdT + (∂u/∂v)Tdv. (2.12)
Еще запишем основное уравнение термодинамики в двух формах (см. лекцию 1):
dq = du +dw, или dq = du + pdv, где dq =схdT в произвольном процессе.
Пусть х = v = const, т.е. конкретизируем изохорный процесс (dv = 0), и тогда схdT = cvdT = du, т.е.
сv = (∂u/∂T)v.
После подстановки этого выражения в (2.12) получаем:
du = cvdT + (∂u/∂v)Tdv. (2.13)
Получили очень важный результат в виде (2.13) - уравнение для расчета изменения внутренней энергии. Если рассмотреть еще энтальпию h(s,v), снова сделать замену переменных h(T,p) с помощью уравнений состояния, далее провести процесс х = p = const над рабочим телом, то получим уравнение для расчета изменения энтальпии:
dh = cpdT + (∂h/∂p)Tdp. (2.14)
Предлагаем студентам проделать эту процедуру.
Уравнения (2.13) и (2.14) справедливы для любых веществ и любых процессов c рабочим телом.
3.1.1. Идеальный газ.
Определение. Идеальным газом называется такое состояние вещества, при котором можно пренебречь силами взаимодействия между молекулами этого вещества.
В этом определении понятия идеального газа подчеркивается, что одно и тоже вещество может быть в любом состоянии, в том числе и в состоянии идеального газа. Например, воздух при обычных условиях (давление и температура – атмосферные) – является идеальным газом. Тот же воздух в жидком состоянии уже не идеальный газ. Пары воды в составе атмосферного воздуха – идеальный газ, а вода в состоянии близком к кипению или конденсации – нет.
В первой лекции было дано определение понятия уравнения состояния: это функциональная зависимость потенциала взаимодействия системы какого-то рода от всех координат состояния. Для термодеформационной системы (а это и есть предмет изучения технической термодинамики) имеем ровно два уравнения состояния:
T = T(s,v) и p = p(s,v). (2.15.1)
Конкретный вид этих зависимостей предоставляют физики для каждого индивидуального рабочего тела (вещества).
Как показано в лекции 1, можно провести несложную замену переменных:
T = T(s,v) → s = s(T,v) → p(s(T,v),v) = p(T,v).
И получаем другую пару уравнений состояния:
T = T(s,v) и p = p(T,v). (2.15.2)
Чисто исторически получилось так, что одно из этих уравнений состояния появилось на свет задолго до появления понятия энтропии и включает в свой состав легко измеряемые в опытах параметры p, v,T, формализуемые в уравнение p = p(T,v)
Вначале уравнение состояния идеального газа было получено экспериментально для условий с небольшими давлениями и температурами. В дальнейшем это уравнение было получено строго на основании молекулярно-кинетической теории газов.
Для 1 кг вещества уравнение состояния идеального газа p = p(T,v) имеет вид:
pv = RуТ. (2.16.1)
Для произвольного количества вещества:
pV = mRуT. (2.16.2)
Если в ряду произвольных количеств вещества выбирается молярное количество, то:
pV΄ = nRT. (2.16.3)
В этих 3х уравнениях p, н/м2, v, м3/кг,T, К – параметры состояния, Rу = 8314/μ Дж/кгК, R = 8314 Дж/кмольК – универсальная газовая постоянная, V – геометрический объем, который занимает вещество, м3, V΄ - его молярный объем нм3/кмоль, m – масса, кг, n – кмоль количество вещества, μ – мольная масса вещества, кг/кмоль.
Условие критерия стабильности (см. первую лекцию), который определяет принцип достоверности построения любого уравнения состояния, выполняется для pv = RуT:
p = RуT/v → (∂(-p)/∂v)T = RуT/v2 ≥ 0.
Еще раз вернемся к основному уравнению термодинамики:
dq = du + pdv → cxdT = cvdT + pdv и
рассмотрим частный случай: рабочее тело находится в состоянии идеального газа и совершается процесс х = p = const. Тогда из предыдущего уравнения следует, что
cp = cv + p(∂v/∂T)p и pv = RуT → v = (R у/p)T → (∂v/∂T)p = Rу/p.
Окончательно, получаем
cp = cv + Rу, и, конечно, cp > cv . (2.17)
Соотношение между теплоемкостями (2.17) в термодинамике носит название закона Майера. Из него следует, что на практике достаточно определить только одну теплоемкость cp или сv, чтобы сразу найти другую. И не будем забывать, что закон Майера справедлив только для идеального газа. Для реальных веществ с другими уравнениями состояния можно лишь говорить, что cp > cv.
Замечание. Уравнение Майера справедливо не только для истинных теплоемкостей, но и для средних. Дело в том, что операция усреднения (2.10) в (2.17) постоянной величины Rу дает в результате саму постоянную.
.
Как ясно из выведенных уравнений (2.13) и (2.14), внутренняя энергия и энтальпия зависят от свойств веществ. Действительно, первое слагаемое включает теплоемкость в явном виде, а во втором слагаемом она же входит в неявном виде как u = u(cv, T). Одновременно, свойства веществ отражаются уравнениями состояния u = u(s,v) и h = h(s,v). Следовательно, оценку роли u и h и их связи с поведением рабочих тел можно установить только, если известны уравнения состояния конкретного вещества (рабочего тела).