Разветвляющиеся программы и операторы управления

С п р а в о ч н а я и н ф о р м а ц и я

Рис.1.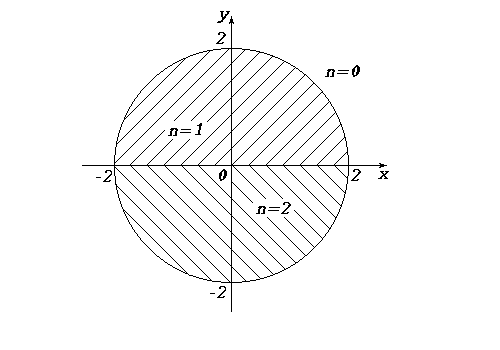

В рассмотренных ранее программах были реализованы линейные алгоритмы, которые требовали последовательного выполнения операций. Однако существует класс задач, решение которых предполагает наличие нескольких путей получения конечного результата. Например, при решении квадратного уравнения требуется анализировать величину дискриминанта и, в зависимости от его знака, принимать решение о наличии и кратности действительных корней. Поэтому в алгоритме решения должны существовать по крайней мере два взаимоисключающих пути получения конечного результата. Эти пути принято называть ветвями алгоритма, а реализующие его программы - разветвляющимися.

Разветвляющийся алгоритм можно продемонстрировать на примере решения следующей задачи. В компьютер вводятся значения переменных X и Y, представляющие собой координаты точки M(x, y) на плоскости xOy (смотри рисунок 1). Вся плоскость xOy разбита на три области, каждая из которых имеет признак n – номер от 0 до 2-х. Требуется разработать алгоритм и составить программу идентификации области, в которую попала точка M. Точки границ отнести к области с большим номером.

Решение поставленной задачи может быть описано следующей последовательностью действий:

1. Ввести значения x и y;

2. Если длина радиуса-вектора точки M(x, y) больше радиуса окружности, ограничивающей области с номерами 1 и 2, то перейти к пункту 3. В противном случае перейти к пункту 4;

3. Присвоить переменной n значение 0 и перейти к пункту 7;

4. Если y больше 0, то перейти к пункту 5, иначе перейти к пункту 6;

5. Присвоить переменной n значение 1 и перейти к пункту 7;

6. Присвоить переменной признака области n значение 2;

7. Вывести значения x, y и n.

Данное описание неудобно, поэтому при разработке разветвляющихся программ рекомендуется составлять блок-схему алгоритма, так как это позволяет получить наглядную схему его функционирования и избежать ошибок. Под блок-схемой понимают графическое отображение алгоритма программы, где каждой операции соответствует свой образ, а последовательность решения изображается соединяющими их линиями. Символьное обозначение операций приведено ниже в таблице.

Выполняемая операция	Образ
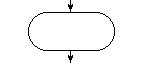
Начало и окончание работы алгоритма или программы
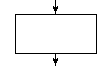
Оператор или группа операторов, изменяющих значение данных
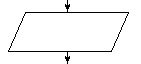
Операторы ввода-вывода данных
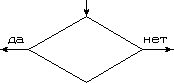
Оператор условного перехода

Внутри каждого элемента блок-схемы в произвольной форме описывается выполняемая операция.

Блок-схема вышеописанного алгоритма приведена на рисунке 2.

Для создания программ, реализующих такие разветвляющиеся алгоритмы, используются операторы безусловного и условного переходов, влияющие на последовательность выполнения операторов.

Оператор безусловного перехода позволяет передать управление любому выполняемому оператору программы. Общая форма оператора

Go to метка

где метка – метка оператора, которому передается управление.

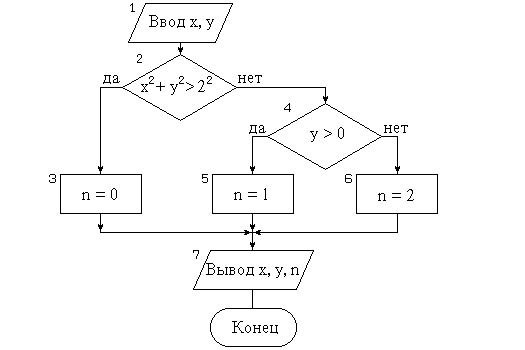
Рис.2.

Выполняемый оператор, непосредственно следующий за оператором безусловного перехода, должен иметь метку, иначе на него невозможно передать управление

Go to 10

А = D + B

10 C = E - A

В данном фрагменте оператор безусловного перехода передает управление оператору C=E-A с меткой 10, минуя оператор A=D+B.

Оператор условного перехода служит для выбора одного из 0нескольких возможных продолжений процесса выполнения программы в зависимости от выполнения некоторого условия.

Оператор условного перехода позволяет использовать в каждой из своих расчетных ветвей не один оператор, а блоки операторов. Общая форма оператора