- •Министерство общего и профессионального образования российской федерации московский государственный технический университет (мами) Кафедра "Прикладная и вычислительная математика"
- •Программирование на языке Фортран
- •Основные понятия. Программирование расчетов по формулам
- •Real*4 – ранг 3
- •Ввод-вывод информации
- •Разветвляющиеся программы и операторы управления
- •If ( выражение ) Then
- •Программирование циклов
- •C *** Конец внутреннего цикла ***
- •Обработка массивов
- •Подпрограммы
Real*4 – ранг 3
Real*8 – ранг 4
Например:
-
5*ROT
– дает результат Real*4;
I/10
– Integer*4;
J + 0.2D+6
– Real*8;
*** Замечания: – в сложных арифметических выражениях тип результата определяется поэтапно, для каждой отдельной операции, например
(N+1) * A
Первая операция – N+1 – дает целый результат, так как оба операнда целого типа. Вторая операция – умножение результата первой операции на А – дает вещественный результат, так как переменная А вещественного типа. Окончательный результат выражения Real*4.
– неучет типов операндов арифметического выражения может привести к неожиданным результатам, например
5 / 2 * 10 = 20; 64**(1 / 3) = 1;
5 / 2.* 10 = 25.0; 64**(1. / 3) = 4.0 .
Простое логическое выражение определяет соотношение между сравниваемыми величинами. Оно представляет собой логические константы и переменные или арифметические выражения, соединенные символами логических отношений, что позволяет записывать необходимые условия. Выделяют следующие логические отношения:
-
.EQ. (= =)
– равно;
.NE.(/= )
– не равно;
.GT. (>)
– больше;
.LT. (<)
– меньше;
.GE. (>=)
– больше или равно
(не меньше);
.LE. (<=)
– меньше или равно
(не больше).
Например, результатом выполнения логического выражения A.LT.B. будет .TRUE. (истина), если A<B, или .FALSE. (ложь), если AB.
Простые логические выражения могут быть объединены в сложные с помощью логических операций .NOT. - "не", .AND. - "и" и .OR. - "или". При вычислении логических выражений используется следующий порядок выполнения операций. Сначала выполняются операции отношения .EQ., .NE., .GT., .GE., .LT. и .LE., а затем .NOT., .AND. и .OR.. Например, условие принадлежности величины X отрезку [-1, 3/2] или интервалу ]3, 8[ будет записываться в виде
X.GE.-1..AND.X.LE.1.5.OR.X.GT.3..AND.X.LT.8.
Для изменения порядка выполнения логических операций или повышения степени их наглядности используются скобки:
((X.GE.-1.).AND.(X.LE.1.5)).OR.(X.GT.3..AND.X.LT.8.)
Текстовое выражение служит для обработки символьных констант и переменных. Для них определена только одна операция – конкатенация – слияние символьных констант и переменных, обозначающаяся символами "//".
Например выражение '1 + 1 ='//' 2' дает '1 + 1 = 2'.
Встроенные библиотечные функции – это программы для вычисления элементарных математических функций (например, sin х, cos х и др.), которые хранятся в библиотеке математических программ Фортрана. Для обращения к функции в арифметическом выражении требуется указать имя функции и далее в круглых скобках фактический параметр в форме константы, переменной или выражения. Ниже в таблице приведены некоторые часто используемые библиотечные функции.
-
Название
функции
Математическое
обозначение
Обозначение функции
в Фортране
Показательная функция
ex
Exp(x)
Натуральный логарифм
ln x
Log(x)
Десятичный логарифм
lg x
Log10(x)
Синус
sin x
Sin(x)
Косинус
cos x
Cos(x)
Тангенс
tg x
Tan(x)
Арксинус
arcsin x
ASin(x)
Арккосинус
arccos x
ACos(x)
Арктангенс
arctg x
ATan(x)
Квадратный корень
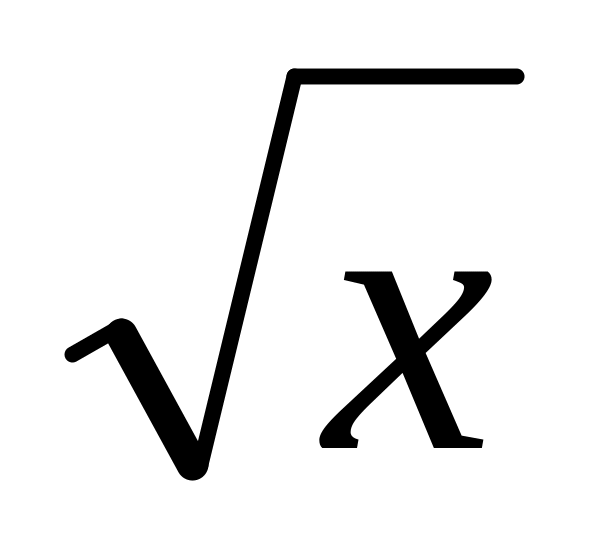
Sqrt(x)
Абсолютное значение
x
Abs(x)
Целая часть числа
[x]
Int(x)
При использовании функций следует учитывать, что:
тригонометрические функции используют аргумент только в радианной мере;
аргументы, приведенных в таблице функций, и результаты их вычислений имеют вещественный тип;
Оператор присваивания – простейший выполняемый оператор Фортрана. Он не имеет ключевого слова и форма его записи имеет вид:
переменная = выражение
Действие оператора состоит в том, что переменная, стоящая слева от символа "=", получает значение, равное результату выполнения выражения, записанного справа. Например
A = c i = i + 1
Res_1 = (1.0 + Exp(x+1))/(x**2 + 1.) Str = 'МГТУ (МАМИ)'
После вычисления выражения его результат, независимо от типа, приводится к типу переменной. Например, оператор L = 12.1 / 10.4 даст результат, равный единице.
Пример выполнения задания. Вычислить значение функции
![]() при
x
= 1.5 .
при
x
= 1.5 .
Программа
program lab_1
implicit none
Real x, y
x=1.5
y= 4.*x/(x*x+1.);
print *, 'x=',x,' y=', y
end program
Результат
З а д а н и е к л а б о р а т о р н о й р а б о т е
Составить программу для вычисления по формулам. Программу протестировать на приведенных данных. Значения аргументов задавать с помощью оператора присваивания. Результаты расчета вывести на экран монитора.
1 |
При x = 0.5, y = 4.62759Е02 |
2 |
При x = 1, z = 0.97728 |
3 |
При x = 1.7, y = 1.370529 |
4 |
При x = 0.6, v = 431.1837 |
5 |
При x = 0.4, y = 1.17128 |
6 |
При x = 1, z = 0.6947773 |
7 |
При x = 1, z = 0.1254594 |
8 |
При x = 0.3, y = 0.1220199 |
9 |
При x = 1, y = 4.225864 |
10 |
При x = 1.7, v = 2.943459 |
11 |
При x = 1.5, y = 0.1792445 |
12 |
При x = 1, z = 0.5330063 |
13 |
При x = 1.3, y = 6.9011946 |
14 |
При x = 0.8, v = 0.3356272 |
15 |
При x = 0.8, y = 0.296262 |
16 |
При x = 1.5, z = 1.9183795E-03 |
17 |
При x = 0.5, z = 0.1372674 |
18 |
При x = 0.3, y = 9.580337E-02 |
19 |
При x = 1, y = 1.145531 |
20 |
При x = 0.5, v = 1.293568 |
21 |
При x = 0.3, y = 1.187293 |
22 |
При x = 1, z = 05133697 |
23 |
При x = 1.3, Y = 0.6068606 |
24 |
При x = 0.5, v = 2.377286 |
25 |
|
26 |
При x = 0.5, z = 1.441137 |
27 |
При x = 1, z = 4.4465311E-02 |
28 |
При x = 0.3, y = 0.1773368 |
29 |
При x = 1, y = 1.289237 |
30 |
При x = 0.7, v = 1.044279 |
Л А Б О Р А Т О Р Н А Я Р А Б О Т А № 2







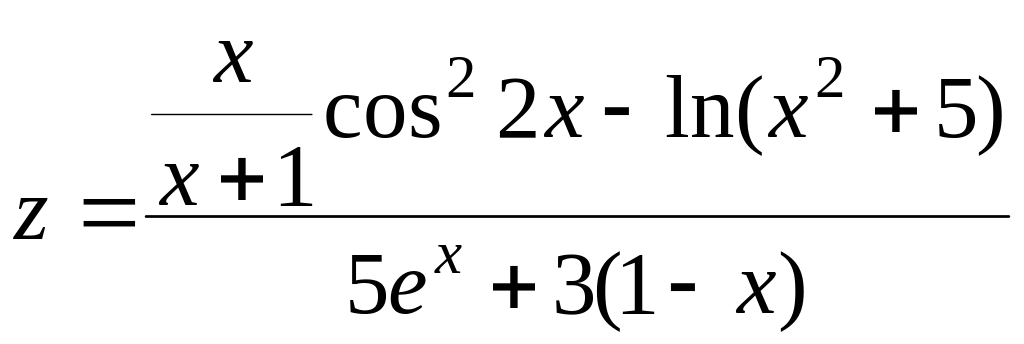




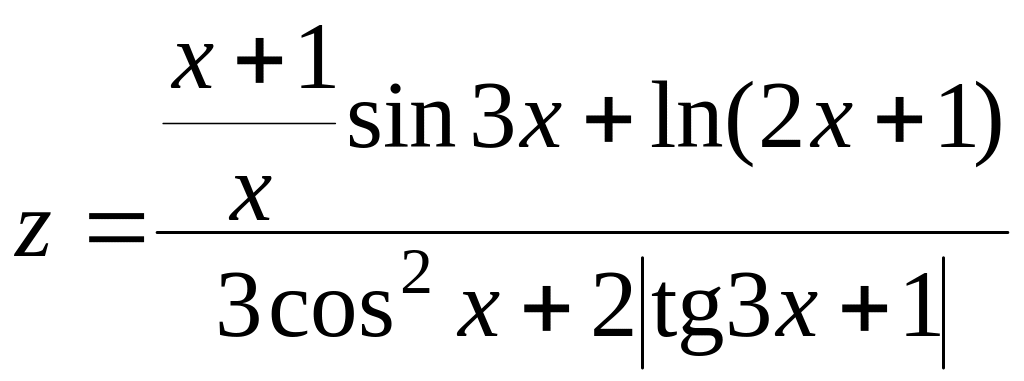
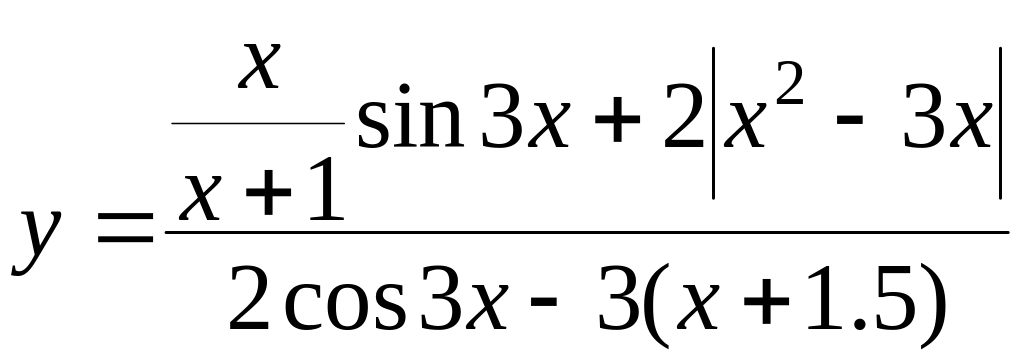





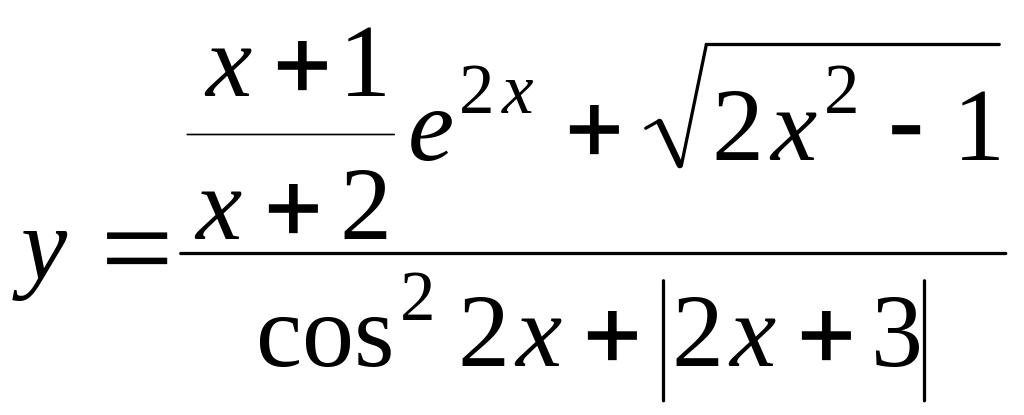
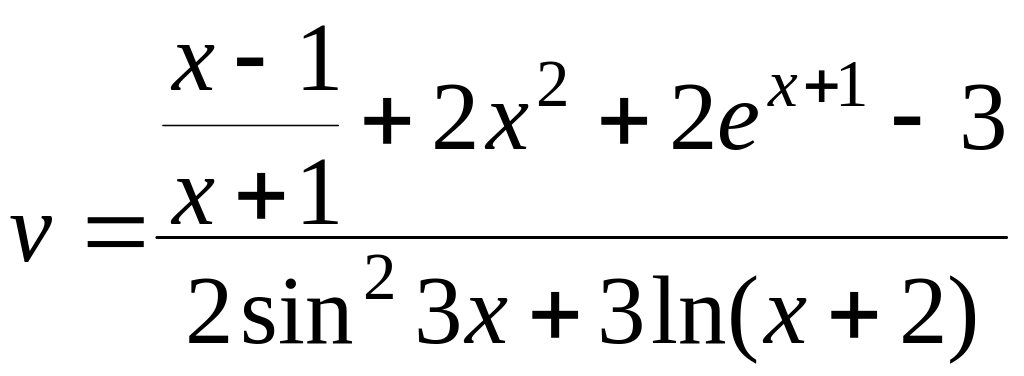




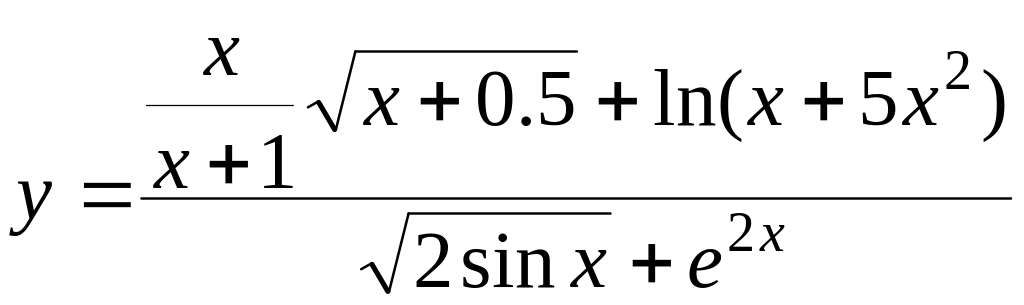 При
x
= 0.4,
y
= 1. 458705
При
x
= 0.4,
y
= 1. 458705