8. Методы детерминированного факторного анализа

Идея детерминированного факторного анализа заключается в разложении общей вариации результатирующей переменной у на независимые компоненты, каждая из которых характеризуется влиянием того или иного фактора х_i или взаимодействием целого ряда факторов. Основные предпосылки проведения детерминированного факторного анализа состоят в следующем:

• определение детерминированной модели путем логического анализа;

• наличие функциональной (жесткой) связи между факторами и результативным показателем;

• невозможность разделения действующих факторов, которые не поддаются объединению в одной модели;

• изучение взаимодействий в короткий промежуток времени, при котором внутренние свойства исследуемого объекта не могут измениться.

Способы детерминированного факторного анализа основываются на методе элиминирования. Элиминировать – это, значит, устранить, отклонить, исключить воздействие всех факторов на величину результативного показателя кроме одного. При моделировании детерминированных факторных систем необходимо выполнять ряд требований.

Факторы, которые включаются в модель, и сами модели должны иметь определенно выраженный характер, реально существовать, а не быть придуманными абстрактными величинами или явлениями.

Факторы, которые входят в систему, должны быть не только необходимыми элементами формулы, но и находиться в причинно-следственной связи с изучаемыми показателями. Иначе говоря, построенная факторная система должна иметь познавательную ценность.

Все показатели факторной модели должны быть количественно измеримы, т. е. Должны иметь единицу измерения и необходимую информационную обеспеченность.

Факторная модель должна обеспечивать возможность измерения влияния отдельных факторов, это значит, что в ней должна учитываться соразмерность изменений результативного и факторного показателей, а сумма влияния отдельных факторов должна равняться общему изменению результативного показателя.

Факторные модели в детерминированном анализе обязательно должны подчиняться следующему условию: сначала в моделях просчитывается влияние количественных факторов, а затем качественных. Если же имеется несколько количественных и качественных показателей, то сначала следует измерить величину факторов первого уровня подчинения, а потом более низкого. Выполнение данного требования позволяет получить более точные результаты, и избежать недостатков метода элиминирования.

Сферу применения приемов детерминированного факторного анализа в систематизированном виде можно представить в следующем виде:

Таблица 2.3.

Сфера применения методов детерминированного факторного анализа для различных типов моделей

Способ	Модели
	мультипликативные	аддитивные	кратные	смешанные
Цепной подстановки	+	+	+	+
Абсолютных разниц	+	-	-	У=а(в-с)
Интегральный	+	-	+	У=а/xi
Логарифмирования	+	-	-	-
Индексный	+	-	+	-

Способ цепной подстановки является наиболее универсальным, так как его можно применять для всех типов детерминированных факторных моделей. Сущность данного способа заключается в определении влияния отдельных факторов на изменение величины результативного показателя путем постепенной замены базисной величины каждого факторного показателя в объеме результативного, на фактический в отчетном периоде.

Например, возьмем трехфакторную мультипликативную модель типа:

у = авс, тогда влияние факторов можно определить следующим образом:

у₁ = а₀в₀с₀ у₂ = а₁в₀с₀ у₂ - у₁ – влияние фактора а

у₃ = а₁в₁с₀ у₃ - у₂ – влияние фактора в

у₄ = а₁в₁с₁ у₄ - у₃ – влияние фактора с

Пример В таблице 2.4. приведены данные об использовании основных средств в Тамбовской области за 2004-2005 годы. На основании приведенной информации (табл.2.4.) определим, как повлияло изменение объема основных средств (количественный, экстенсивный фактор) и отдачи (качественный, интенсивный фактор) на объем валового регионального продукта.

Таблица 2.4.

Показатели отдачи основных средств по Тамбовской области

(млн. руб.)

Показатели	2004	2005	Отклонение	Темп роста %
Валовый региональный продукт	56775,0	64538,7	7763,7	113,7
Остаточная стоимость основных средств	118768,2	130387	11618,8	109,8
Объем ВРП в расчете на 1 руб. основных средств	0,478	0,495	+0,017	103,6

Исходная модель:

ВРП=ОС*О

1) Расчет влияния факторов, с помощью метода цепных подстановок:

ВРП₁=ОС₀*О₀= 118768,2*0,478= 56775,0

ВРП₂=ОС₁*О₀= 130387,0*0,478= 62325,0

ВРП₃=ОС₁*О₁= 130387,00*0,495= 64538,7

2) Рассчитаем влияние изменения среднегодовой стоимости основных средств на изменение объема ВРП (ВРП₂-ВРП₁)

62325-56775=5550 млн.руб.

Данные расчета показывают, что в результате увеличения стоимости основных средств на 11618,8 млн. руб., прирост объема ВРП составил 5550 млн.руб.

3) Рассчитаем влияние изменения отдачи основных средств на изменение объема ВРП (ВРП₃-ВРП₂)

64538,7 – 62325,0 = 2213,7 млн.руб.

Данные расчета показывают, что в результате увеличения отдачи на 0,017 коп на каждый вложенный рубль в основных средств, прирост объема ВРП составил 2213,7 млн.руб.

4) Таким образом совокупное влияние факторов составило 5550+2213,7=+7763,7 млн.руб.

5) Определим прирост ВРП за счет интенсивного и экстенсивного фактора:

5550:7763,7*100%=71,5% - влияние экстенсивного фактора

2213:7763,7*100%=28,5% - влияние интенсивного фактора

Следовательно, в отчетном периоде объем ВРП на 71,5% вырос за счет экстенсивного и соответственно на 28,5% за счет интенсивного факторов.

Расчет влияния интенсивного и экстенсивного фактора можно определить и другим способом:

При использовании способа абсолютных разниц величина влияния факторов рассчитывается умножением абсолютного прироста на базовую величину факторов, которые находятся справа от него и на фактическую величину факторов, расположенных слева от него. Способ абсолютных разниц применим в мультипликативных и смешанных моделях типа:

у = а(в-с) и у = (а-в)с.

Покажем расчет влияния факторов на мультипликативной модели

у = авс

а = а₁-а₀ в = в₁-в₀ с = с₁-с₀

у₁ = а в₀ с₀ - влияние фактора а

у₂ = а₁ в с₀ – влияние фактора в

у₃ = а₁ в₁ с - влияние фактора с

Рассмотрим алгоритм расчета факторов этим способом в моделях мультипликативно-аддитивного типа.

у=а(в-с)

у₁ = а (в-с) - влияние фактора а

у₂ = а₁ в – влияние фактора в

у₃ = а₁ (-с) - влияние фактора с

Мощным орудием сравнительного анализа региональной экономики являются индексы. Индексный метод основывается на относительных показателях, выражающих отношение уровня данного явления к уровню его в прошлое время или к уровню аналогичного явления, принятому в качестве базы. Индексный метод можно применять в мультипликативных и кратных моделях.

С помощью индексов в региональном экономическом анализе решаются следующие основные задачи:

• оценка изменения уровня явления;

• выявление роли отдельных факторов в изменении результативного признака;

• оценка влияния изменения структуры совокупности на динамику.

В зависимости от степени охвата подвергнутых обобщению единиц изучаемой совокупности индексы подразделяются на индивидуальные и общие. Индивидуальные индексы характеризуют изменения отдельных единиц совокупности. Общие индексы выражают сводные результаты совместного изменения всех единиц, образующих совокупность.

Элиминирование как способ детерминированного факторного анализа имеет существенный недостаток, так расчет влияния факторов производится поочередно, не учитывая совместное воздействие, и даже простая перестановка факторов в модели дает совершенно разные результаты.

Чтобы избавиться от этого недостатка в мультипликативных, кратных и смешанных моделях типа у = а / (в+с) можно использовать интегральный способ расчета. Его сущность заключается в том, что общий абсолютный прирост от взаимодействия факторов раскладывается между ними пропорционально изолированному их воздействию. Приведем алгоритм расчета влияния факторов для разных типов моделей:

1. у = ав

влияние фактора a

влияние фактора b

или

влияние фактора а

влияние фактора b

влияние фактора а

влияние фактора b

влияние фактора с

влияние фактора а

влияние фактора b

влияние фактора с

Таким образом, использование выше перечисленных формул не потребует знания всего процесса интегрирования. Достаточно в эти готовые рабочие формулы подставить необходимые числовые данные и провести соответствующие расчеты.

Еще более высокую точность расчетов для мультипликативных моделей можно получить с помощью способа логарифмирования. С его помощью результат совместного действия факторов распределяется пропорционально доли изолированного влияния каждого фактора на уровень результативного показателя. В отличии от интегрального метода при логарифмировании используются не абсолютные приросты показателей, а индексы их изменения. Алгоритм применения данного способа покажем на трехфакторной мультипликативной модели:

у = а в с

Прологарифмируем обе части уравнения

lg y = lgа + lgв + lgс

Разделим обе части уравнения на lg (у₁/у₀) и умножим на у.

у =  у(а) +  у(в) +  у(с), т.е.

влияние фактора a

влияние фактора b

влияние фактора c

9. Способы стохастического факторного анализа

Выше указанные способы детерминированного факторного анализа используются для функциональных зависимостей, но не менее важную долю в экономических исследованиях занимают стохастические зависимости (корреляционные). При проведении корреляционно-регрессионного анализа выявляется количественная оценка взаимосвязей между факторными и результативными признаками, выявляется наличие и характеристика взаимосвязи, а также направление и форма. Следует помнить, то применение корреляционной зависимости оправдано только в большой массе наблюдений, подчиняющихся закону нормального распределения. Для другого вида взаимозависимостей вероятностного характера оправдано применение непараметрических способов анализа.

Корреляционные связи не являются точными (жесткими) зависимостями, а эти зависимости носят соотносительный характер. Если знание функциональных зависимостей позволяет точно расcчитывать события, например, время восхода и захода солнца ежедневно, время наступления солнечных затмений с точностью до секунды, то при корреляционных связях при одном и том же значении учтенного факторного признака могут быть различные значения результата. Это объясняется наличием других, порой неучтенных факторов, которые действуют на изучаемые социально-экономические явления. Особенность корреляционных связей состоит в том, что их проявление можно заметить не в единичных случаях, а в массе случаев.

Для определения корреляционной связи показателей социально-экономической, финансовой и прочей деятельности необходимо решить две основные задачи:

1. проверить возможность существования взаимосвязи между изучаемыми показателями и придать выявленной взаимосвязи конкретную математическую форму зависимости;

2) установить количественные оценки тесноты взаимосвязи, т.е. силу влияния факторных признаков на результат.

Наиболее разработанными в статистике являются методы изучения парной корреляции, позволяющие определить влияние изменения факторного признака (х) на результативный (у). Чтобы отразить выявляемые взаимосвязи в аналитической форме прибегают к использованию математических функции в виде уравнения прямолинейной и криволинейной зависимости.

Для анализа прямолинейной зависимости применяется уравнение вида:

у_х=а₀+а_1*х

Криволинейная зависимость анализируется с помощью математических функций параболы, гиперболы, показательной, степенной и др.

При анализе корреляционной зависимости между признаками “х” и “у” необходимо:

а) выявить вид функционального уравнения;

б) определить численное выражение их параметров;

в) осуществить проверку вычисленных параметров на их типичность;

г) произвести оценку практической ценности выявленной модели функционального уравнения;

д) определить в какой степени теснота корреляционной (соотносительной) связи между факторами и результатом отличается от функциональной (жесткой) зависимости, и.т.д.

Осуществить это можно путем применения метода группировок и корреляционно-регрессионного анализа влияния изменения (вариации) факторного признака “х” на результативный “у”.

Модель регрессии может быть построена как по индивидуальным значениям признака, так и по сгруппированным данным (таблица № 1). Для выявления связи между признаками по достаточно большому числу наблюдений используется корреляционная таблица на ее основе можно построить не только уравнение регрессии, но и определить показатели тесноты связи.

Искомые параметры уравнения связи находят с помощью способа наименьших квадратов, т.е. при условии что:

Ѕ= → min

Эти расчеты при даже очень большом объеме эмпирических данных с использованием компьютерных технологий, не представляет больших трудностей и времени.

Система нормальных уравнений для нахождения параметров линейной парной регрессии методом наименьших квадратов имеет следующий вид:

;

где

n — объем исследуемой совокупности (число единиц наблюдения),

и – коэффициенты, и – свободные члены

В уравнениях регрессии параметр показывает усредненное влияние на результативный признак неучтенных (не выделенных для исследования) факторов; параметр - коэффициент регрессии, который показывает, насколько изменяется в среднем значение результативного признака при изменении факторного на единицу его собственного измерения. Для нахождения параметров системы нормальных уравнении используется метод определителей. Во-первых представим эту систему в матричном виде:

= =

Определители и получаются заменой свободными членами элементов соответственно первого ( ) и второго ( ) столбцов. Получаем таким образом:

= =

= =

=

=

Система нормальных уравнений для нахождения параметров полулогарифмической парной регрессии методом наименьших квадратов имеет следующий вид:

Аналогично находятся параметры системы уравнений:

При статистическом анализе не линейной корреляции связи возможно применение уравнения регрессии показательной функции:

.

Для решения уравнения производится его логарифмирование:

С учетом требований метода наименьших квадратов составляется система нормальных уравнений:

;

.

Применением к системе метода определителей устанавливаются алгоритмы расчета параметров уравнения:

;

.

Проверка адекватности моделей, построенных на основе уравнений регрессии, начинается с проверки значимости каждого коэффициента регрессии. То есть необходимо сначала проверить параметры уравнения на типичность прежде, чем использовать полученную модель.

Если n (количество групп) меньше 30 то:

;

.

Параметры модели признаются типичными если:

где - это табличное значение, определяемое по распределению Стьюдента (t – распределение) обычно при вероятности α=0,05 и v=n-2.

Измерение тесноты и направления связи является важной задачей изучения и количественного измерения взаимосвязи социально-экономических явлений.

Теснота связи при линейной зависимости измеряется с помощью линейного коэффициента корреляции.

В практике применяются различные модификации формул расчета данного коэффициента:

,

Производя расчет по итоговым значениям исходных переменных, линейный коэффициент корреляции можно вычислить по формуле:

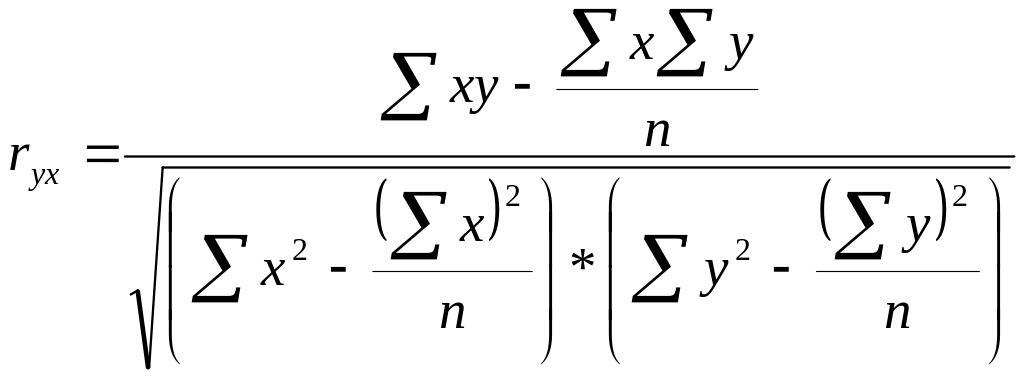
Линейный коэффициент корреляции изменяется в пределах от –1 до +1. Знаки коэффициентов регрессии и корреляции совпадают.

Значимость линейного коэффициента корреляции проверяется на основе t – критерия Стьюдента:

Если расчетное значение (табличное), то гипотеза =0 отвергается, что свидетельствует о значимости линейного коэффициента корреляции, а, следовательно, и свидетельствует о статистической существенности зависимости между факторами “х” и “у”.

Для характеристики степени тесноты связи по линейному коэффициенту корреляции используется шкала Чеддока:

Таблица 2.5

Характеристика силы связи по шкале Чеддока

Теснота связи	0,1-0,3	0,3-0,5	0,5-0,7	0,7-0,9	0,9-0,99
Характеристика степени тесноты связи	слабая	заметная	умеренная	высокая	весьма высокая

Частное от деления факторной (σ²_ух) дисперсии на общую дисперсию (σ²_у) представляет собой показатель (R), указывающий на меру тесноты связи между признаками “х” и “у”, при не линейных зависимостях.

R²= ; тогда R= =

Показатель R² называется индексом детерминации, свидетельствующий насколько значение результативного признака обусловлено влиянием факторного. Чем ближе значение R² к единице, тем сильнее зависимость.

Проверка адекватности всей модели осуществляется с помощью F – критерия Фишера и величины средней ошибки аппроксимации .

где m – число параметров уравнения (при и , т.е. m=2)

V₁=n-m; V₂=m-1.

Индекс корреляции считается типичным если

Значение средней ошибки аппроксимации, определяется по формуле, которая показывает степень влияния на изменение результативного признака неучтенных факторов. Если ошибка аппроксимации не превышает 12-15%, то с построенное уравнение регрессии можно использовать в экономических расчетах.

Расчет частных коэффициентов эластичности позволяет определить на сколько процентов изменяется результативный признак при изменении факторного признака на один процент.

Применение методов корреляционно-регрессионного анализа влияния вариации факторного показателя “x” на результативный “y” рассмотрим на конкретном примере.