
МАТЕМАТИКА
КОНТРОЛЬНЫЕ ЗАДАНИЯ
для студентов-заочников профиля подготовки
080200.6200.13 МЕНЕДЖМЕНТ ОРГАНИЗАЦИИ
080200.6200.07 УПРАВЛЕНИЕ МАЛЫМ БИЗНЕСОМ
КОНТРОЛЬНЫЕ ЗАДАНИЯ
Ниже приведены таблицы номеров задач, входящих в задания на контрольные работы, по учебным планам. Студент должен выполнять контрольные задания по варианту, номер которого совпадает с последней цифрой его номера студенческого билета (шифр).
.
Студенты групп ЗСМ (прием 2012) изучающие высшую математику 2 семестра, выполняют:
Контрольные работы № 1 (1 семестр).
Контрольные работы № 2 (2 семестр).
Вариант |
Контрольная работа №1 |
|
1 |
11 |
51 |
2 |
12 |
52 |
3 |
13 |
53 |
4 |
14 |
54 |
5 |
15 |
55 |
6 |
16 |
56 |
7 |
17 |
57 |
8 |
18 |
58 |
9 |
19 |
59 |
10 |
20 |
60 |
Вариант |
Контрольная работа №2 |
||||||
1 |
91 |
121 |
151 |
161 |
191 |
|
|
2 |
92 |
122 |
152 |
162 |
192 |
|
|
3 |
93 |
123 |
153 |
163 |
193 |
|
|
4 |
94 |
124 |
154 |
164 |
194 |
|
|
5 |
95 |
125 |
155 |
165 |
195 |
|
|
6 |
96 |
126 |
156 |
166 |
196 |
|
|
7 |
97 |
127 |
157 |
167 |
197 |
|
|
8 |
98 |
128 |
158 |
168 |
198 |
|
|
9 |
99 |
129 |
159 |
169 |
199 |
|
|
10 |
100 |
130 |
160 |
170 |
200 |
|
|
Студенты групп ЗСМ (прием 2012) изучающие высшую математику 3 семестра, выполняют:
Контрольная работа № 1 (1 семестр).
Контрольная работа№ 2 (2 семестр).
Контрольная работа № 3 (3 семестр).
Вариант |
Контрольная работа №1 |
|
1 |
11 |
51 |
2 |
12 |
52 |
3 |
13 |
53 |
4 |
14 |
54 |
5 |
15 |
55 |
6 |
16 |
56 |
7 |
17 |
57 |
8 |
18 |
58 |
9 |
19 |
59 |
10 |
20 |
60 |
Вариант |
Контрольная работа №2 |
||||||
1 |
91 |
121 |
151 |
161 |
191 |
|
|
2 |
92 |
122 |
152 |
162 |
192 |
|
|
3 |
93 |
123 |
153 |
163 |
193 |
|
|
4 |
94 |
124 |
154 |
164 |
194 |
|
|
5 |
95 |
125 |
155 |
165 |
195 |
|
|
6 |
96 |
126 |
156 |
166 |
196 |
|
|
7 |
97 |
127 |
157 |
167 |
197 |
|
|
8 |
98 |
128 |
158 |
168 |
198 |
|
|
9 |
99 |
129 |
159 |
169 |
199 |
|
|
10 |
100 |
130 |
160 |
170 |
200 |
|
|
Вариант |
Контрольная работа №3 |
||
1 |
351 |
361 |
371 |
2 |
352 |
362 |
372 |
3 |
353 |
363 |
373 |
4 |
354 |
364 |
374 |
5 |
355 |
365 |
375 |
6 |
356 |
366 |
376 |
7 |
357 |
367 |
377 |
8 |
358 |
368 |
378 |
9 |
359 |
369 |
379 |
10 |
360 |
370 |
380 |
1. Элементы векторной алгебры и аналитической геометрии
11 – 20. Даны координаты вершин пирамиды А1А2А3А4. Найти: 1) длину ребра А1А2; 2) угол между ребрами А1А2 и А1А4; 3) угол между ребром А1А4 и гранью А1А2А3; 4) площадь грани А1А2А3; 5) объем пирамиды; 6) уравнение прямой А1А2; 7) уравнение плоскости А1А2А3; 8) уравнение высоты, опущенной из вершины А4 на грань А1А2А3. Сделать чертеж.
11. А1 (2; 1; –4), А2(1; –2; 3), А3(1; –2; –3), А4(5; –2; 1).
12. А1 (2; –1; 3), А2 (–5; 1; 1), А3(0; 3; –4), А4(–1; –3; 4).
13. А1 (5; 3; 6), А2 (–3; –4; 4), А3(5; –6;8), А4(4; 0; –3).
14. А1 (5; 2; 4), А2(–3; 5; –7), А3(1; –5; 8), А4(9; –3; 5).
15. А1 (7; –1; –2), А2(1; 7; 8), А3(3; 7; 9), А4(–3; –5; 2).
16. А1 (–2; 3; 4), А2(4; 2; –1), А3(2; –1; 4), А4(–1; –1; 1).
17. А1 (0; 4; –4), А2(5; 1; –1), А3(–1; –1; 3), А4(0; –3; 7).
18. А1 (0; –6; 3), А2(3; 3; –3), А3(–3; –5; 2), А4(–1; –4; 0).
19. А1 (2; –1; 3), А2(–5; 1; 1), А3(0; 3; –4), А4(–1; –3; 4).
20. А1 (2; 1; –4), А2(1; –2; 3), А3(1; –2; –3), А4(5; –2; 1).
31 – 40. Привести уравнение кривой второго порядка к каноническому виду, построить график кривой.
31. x2 + у2 – 4x + 2у = 4; 32. x2 – у2 – 4у – 13 = 0;
33. x2 – 4x + 2у + 2= 0; 34. x2 + 4x + 4у2 + 8у – 5 = 0;
35. x2 – 6у2 – 12x + 36у – 54 = 0; 36. 2x2 + 4x + 18у2 – 16= 0;
37. 2x2 + 2у2 + 4x – 8у – 8 = 0; 38. –x + у2 + 2у = 0;
39. 3x2 + 5у2 + 12x – 10у + 2 = 0; 40. 4x2 – 3у2 – 8x – 6у – 11 = 0.
2. Элементы линейной алгебры
51 – 60. Дана система линейных уравнений

Доказать ее совместность и решитьтремя способами: 1) по формулам Крамера; 2) методом Гаусса; 3) средствами матричного исчисления. Проверить правильность вычисления обратной матрицы, используя матричное умножение.
-
51.

52.

53.

54.

55.

56.

57.

58.

59.
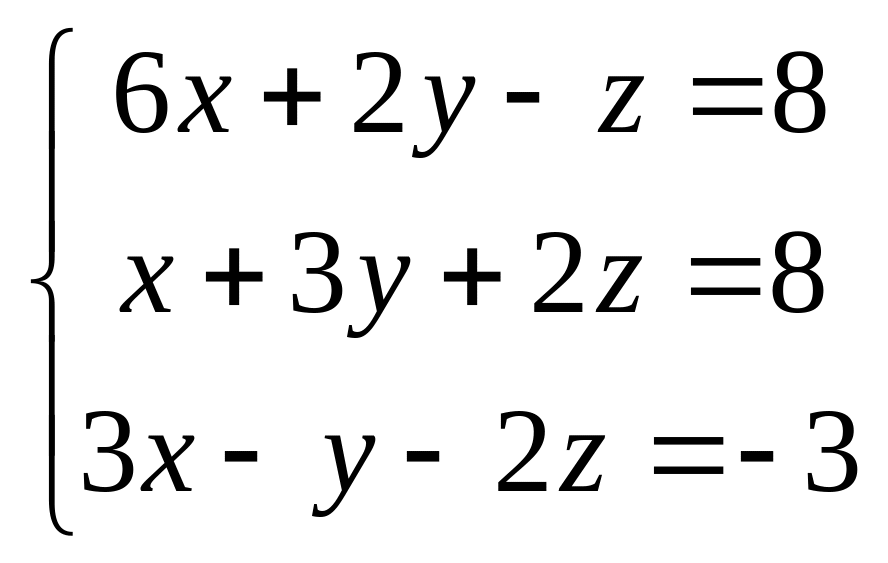
60.

3.Введение в математический анализ
91 – 100. Найти пределы функций, не пользуясь правилом Лопиталя.
91. a)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)![]() ;
д)
;
д)
![]() .
.
92. a)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() .
.
93. a)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
д).
;
д).
![]()
94. a)
![]() ; б)
; б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() .
.
95. a)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() .
.
96. a)
![]() ;
б)
;
б)
![]() .
.
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() .
.
97. a)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() .
.
98. a)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() .
.
99. a)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() .
.
100. a)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() .
.
4. Производная и еЁ приложения
121 - 130. Найти производные
![]() данных функций.
данных функций.
121. |
a)
|
б)
|
|
в)
|
г)
|
|
д)
|
|
122. |
а)
|
б)
|
|
в)
|
г)
|
|
д)
|
|
123. |
а)
|
б)
|
|
в)
|
г)
|
|
д)
|
|
124. |
а)
|
б)
|
|
в)
|
г)
|
|
д)
|
|
125. |
а)
|
б)
|
|
в)
|
г)
|
|
д)
|
|
126. |
а)
|
б)
|
|
в)
|
г)
|
|
д)
|
|
127. |
а)
|
б)
|
|
в)
|
г)
|
|
д)
|
|
128. |
а)
|
б)
|
|
в)
|
г)
|
|
д)
|
|
129. |
а)
|
б)
|
|
в)
|
г)
|
|
д)
|
|
130. |
а)
|
б)
|
|
в)
|
г)
|
|
д)
|
|
5. Приложения дифференциального
исчисления
151 – 160. Исследовать методами
дифференциального исчисления функцию
![]() и, используя полученные результаты,
построить её график.
и, используя полученные результаты,
построить её график.
151.
![]() .
152.
.
152.
![]() .
.
153.
![]() .
154.
.
154.
![]() .
.
155.
![]() .
156.
.
156.
![]() .
.
157.
![]() .
158.
.
158.
![]() .
.
159.
![]() .
160.
.
160.
![]() .
.
6. Дифференциальное исчисление функций
нескольких переменных
161 – 170. Найти а)
![]() ;
б)
;
б)
![]() .
.
161. |
a)
|
б)
|
162. |
а)
|
б)
|
163. |
а)
|
б)
|
164. |
а)
|
б)
|
165. |
а)
|
б)
|
166. |
а)
|
б)
|
167. |
а)
|
б)
|
168. |
а)
|
б)
|
169. |
а)
|
б)
|
170. |
а)
|
б)
|
191 – 200. Даны функция
![]() ,
точка
,
точка
![]() и вектор
и вектор
![]() .
Найти: 1) grad z в точке А; 2) производную
в точке А по направлению вектора
.
Найти: 1) grad z в точке А; 2) производную
в точке А по направлению вектора
![]() .
.
191.
![]()
192.
![]()
193.
![]()
194.
![]()
195.
![]()
196.
![]()
197.
![]()
198.
![]()
199.
![]()
200.
![]()
