
- •Основные понятия и классификация моделей
- •Системный подход у управлению зи.
- •Условия эффективности системы зи (сзи).
- •Этапы управления сзи:
- •Системные принципы создания комплексной системы зи
- •Принципы и методы построения им.
- •Основные методы имит.Моделирования
- •Математические методы моделирования инф.Процессов и систем
- •Случайные события и их имитация.
- •Имитация случайных величин
- •Метод Неймана (режекции)
Имитация случайных величин
Моделирование случайных факторов.
Слуяайные факторы в зависимости от их природы могут быть отражены в модели как случайные события, случайные величины (дискрет.или непрер) или как случайные функции (процессы).
Датчики, которые использ, должны обладать след.св-ми:
-Равномерность
-Стохастичность (случайность)
-Независимость.
Проверка сводится к построению гистограмм последовательности СЧ.
Проверка равномерности м.б. выполнена с помощью гистограммы относительных частот генерируемой СВ. чем ближе огибающая гистограммы к прямой, тем в большей степени генерируемая послед-ть отвечает требованию равномерности распределения.
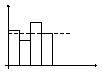
9.10.12.
Проверка стохастичности.
Рассмотрим один из основных методов – метод комбинаций. Суть его сводится к следующему: выбирают достаточно большую последовательность случайных чисел xi и для нее определяют вероятность появления в каждом из xj ровно j единиц.
При попадании r в интервал [0, Pc] считают, что событие А наступило, в противном случае – не наступило.
Метод интерпретации.
Основан на трактовке моделируемого закона распределения. Например, биномиальное распределение описывает число успехов в n независимых испытаниях с вер-тью успеха в каждом испытании Р и вероятностью неудачи g=1-P.
При моделировании этого распределения с помощью метода интерпретации выбирают n независимых С, равномерно распределенных на интервале [0,1], и количество тех из них, которые меньше Р. Это число является моделируемой СВ.
Имитационное модел-ние явлений и объектов, формальное описание которых возможно с помощью представления их в виде СВ с заданным законом распределения основывается на использовании СЧ с равномерным законом распределения. Такие преобр-я могут быть осуществлены с помощью метода обр. функции, предельных теорем теории вер-ти, приближенных методов и т.д.
Метод обр.функции
Пусть непрерывная случ.величина (СВН) η задана своим законом распределения:
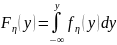 ,
,
Где
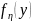 – плотность распределения вероятностей,
– плотность распределения вероятностей,
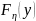 – функция
распределения вероятностей.
– функция
распределения вероятностей.
Доказано,
что случ.величина
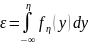 распределена равномерно на интервале
(0, 1). Отсюда следует, что искомое значение
y
может быть определено из уравнения:
распределена равномерно на интервале
(0, 1). Отсюда следует, что искомое значение
y
может быть определено из уравнения:
 , (**)
, (**)
Которое эквивалентно уравнению:
 , (*)
, (*)
Где
y
– значение случ.величины η, а х – значение
случ.величины ε. Решение уравнения (*)
можно записать в общем виде через
обр.функцию:
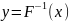 .
.
Основная проблема заключ.в том, что интеграл (**) не всегда берется, а уравнение (*) не всегда решается аналитическими методами.
Пример.
Получить в соответствии с методом обр.функции преобразование, позволяющее вычислить значение СВ η, распределенной по показательному закону.
Решение.
Показательный закон характеризуется функцией плотности:
 .
.
Воспользуемся методом обр.функции, вычислим интеграл (**) и получим уравнение вида (*):
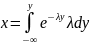 или
или
 .
Тогда
.
Тогда
 ,
прологарифмировав ур-ние через y,
будем иметь:
,
прологарифмировав ур-ние через y,
будем иметь:
 .
(***)
.
(***)
Получая значение х с помощью датчика равномерно распределенных СЧ на интервале (0,1) можно получить значения y в соответствии с выражением (***). Показательный закон распределения особенно часто использ.для исследования СМО и определения показателей надежности систем.
Пример 2.
Получить преобразование в соответствии с методом обратной функции СВ η вычислить значение СВ η, распределенной по закону Вейбулла.
Решение.
Плотность распределения такой СВ имеет вид:
 ,
,
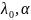 – параметры
закона распределения, введем обозначение
– параметры
закона распределения, введем обозначение
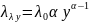 .
Нетрудно вывести уравнение вида (*). Для
данного распределения оно имеет вид:
.
Нетрудно вывести уравнение вида (*). Для
данного распределения оно имеет вид:
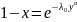 .
.
Следовательно,
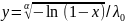 .
.
распределение
Вейбулла имеет место при исследовании
отказов элементов оборудования, возникших
в рез-те износа и старения. Параметр
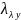 носит название и имеет смысл интенсивности
отказов.
носит название и имеет смысл интенсивности
отказов.
При α=1 закон Вейбулла совпадает с показательным, при α<1 интенсивность отказа является монотонно убывающей, а при α>1 – монотонно возрастающей функции.
