Лекции по сопромату2 / SOPROMAT_lekcii1

Лекция № 10. Влияние различных факторов на механические характеристики материалов

Зависимость механических характеристик конструкционных материалов от их химического состава, внешних условий и условий нагружения весьма многообразна; отметим наиболее существенные, характерные для типичных условий эксплуатации конструкций.

Влияние содержания углерода. Введение различных легирующих добавок в металлы позволяет значительно повысить прочностные характеристики сплавов. На рис. 1 показано влияние процентного содержания углерода на механические свойства конструкционной стали. Как видно, с увеличением содержания углевода, временное сопротивление повышается в несколько раз; однако при этом значительно ухудшаются

пластические свойства; относительное удлинение и относительное сужение 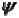при разрыве уменьшаются.

Рис.1. Влияние процентного содержания углерода

Влияние температуры окружающей среды. Повышенные температуры оказывают существенное влияние на такие механические характеристики конструкционных материалов, как ползучесть и длительная прочность. Ползучестью называют медленное непрерывное возрастание пластической (остаточной) деформации под воздействием постоянных нагрузок. Длительной прочностью называется зависимость разрушающих напряжений (временного сопротивления) от длительности эксплуатации. Свойства ползучести и длительной прочности проявляются у углеродистых сталей при Т >300oС, для легированных сталей при Т>350oС. для алюминиевых сплавов при Т>100oС. Некоторые материалы проявляют эти свойства и при обычных температурах.

Мерой оценки ползучести материала является предел ползучести — напряжение, при котором пластическая деформация за определенный промежуток времени достигает заданной величины. В некоторых случаях сопротивление ползучести оценивается величиной скорости деформации по прошествии заданного времени. При обозначении предела ползучести указывается величина деформации, время и температура испытаний. Например, для жаропрочного сплава ХН77ТЮР при температуре 700oС за время 100 часов и деформации ползучести 0,2% предел ползучести составляет 400

МПа: .

Ползучесть сопровождается релаксацией напряжений — самопроизвольным уменьшением напряжений с течением времени при неизменной деформации. Скорость релаксации напряжений возрастает при повышении температуры. Мерой скорости релаксации служит время релаксации—промежуток времени, в течение которого напряжение уменьшается по сравнению с начальным значением в е=2,718 раза.

Прочность материала при повышенных температурах оценивается пределом длительной прочности — напряжением, при котором материал разрушается не ранее заданного времени. При обозначении предела длительной прочности указывается продолжительность нагружения и температура испытания. Так, для сплава ХН77ТЮР при температуре 700oС и времени 1000 часов предел длительной прочности составляет

. При кратковременных испытаниях для этого же сплава при температуре 700oС пределы прочности и текучести соответственно равны:

.

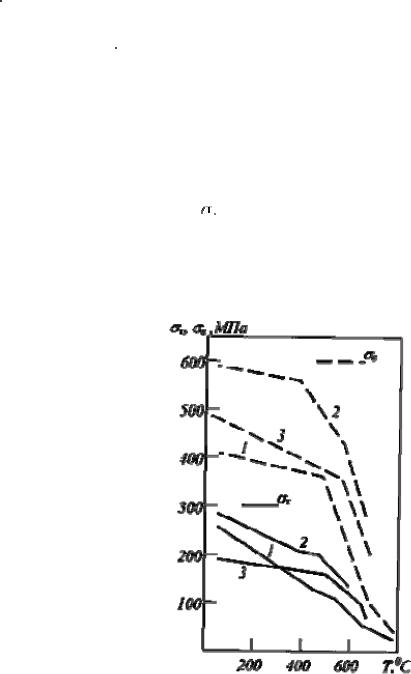
Влияние повышенных температур на характеристики прочности и пластичности можно проследить на рис. 2 и 3, где представлены осредненные результаты экспериментов для 1—углеродистой стали, содержащей 0,15% углерода; 2—0,40% углерода, 3—хромистой стали. Прочность углеродистых сталей с повышением температуры до 650—700oС снижается почти в десять раз. Наиболее резкое снижение

наблюдается для алюминиевых сплавов. Наибольшими значениями при высоких температурах обладают литые жаропрочные сплавы, содержащие 70—80% никеля.

Снижение пределов текучести с повышением температуры происходит примерно так

же, как и снижение 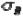. Для углеродистых сталей характерным является ухудшение пластических свойств (охрупчивание) при температурах около 300oС (кривая 2 на рис. 3).

Рис.2. Влияние температуры на упругие свойства

Рис.3. Влияние температуры на пластические свойства

Влияние температур на упругие свойства. Температурный коэффициент линейного расширения и температурный коэффициент модуля упругости

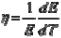связаны между собой соотношением

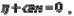или

где r и m — постоянные, характеризующие параметры кристаллической решетки. На рис. 4 приведена зависимость безразмерного модуля упругости Е/Е0 некоторых конструкционных материалов от температуры (E0— модуль упругости материала при обычной температуре): 1 — нержавеющая сталь; 2 — алюминиевые сплавы, 3 — углеродистые стали, 4 — титановые сплавы.

Для сталей с повышением температуры испытаний с 25 до 450oС модули упругости Е и G уменьшаются на 20—40%, при этом, начиная с 300—400oС наблюдается расхождение между значениями модулей, определенными при статических и динамических испытаниях.

Изменение модулей упругости при малый колебаниях температуры (от –50 до +50oС) незначительно и им обычно пренебрегают.

Рис.4. Зависимость модуля упругости от температуры

Лекция № 11. Основные понятия теории надежности конструкций

ПОСТАНОВКА ЗАДАЧ ТЕОРИИ НАДЕЖНОСТИ

Согласно ГОСТ 27.002—89 «Надежность в технике. Термины и определения» надежность конструкции есть свойство сохранять во времени способность к выполнению требуемых функций в заданных режимах. Одним из основных понятий Теории надежности конструкций является понятие предельного состояния. Условие прочности по существу есть условие обеспечения прочностной надежности.

Основной особенностью реальных условий эксплуатации машин и конструкций является случайный характер взаимодействия с окружающей средой. Это проявляется в том, что мы не можем достоверно предвидеть все типы внешних нагрузок и их величины, которые могут встретиться в процессе эксплуатации. Кроме того, источником неопределенности могут быть случайные свойства материалов. Например, предельное

напряжение , входящее в условие прочности, по своей природе является случайным. Его величина зависит от многих факторов: марки материала, технологии изготовления, размеров детали или конструкции, условий эксплуатации и др. Случайный характер механических свойств материалов наглядно проявляется при испытаниях, обнаруживающих значительный разброс экспериментальных данных. Источник неопределенности связан также с разбросом размеров при изготовлении конструкций: в принципе невозможно выдержать абсолютно точно геометрические параметры конструкции, при их изготовлении допускаются некоторые отклонения.

В случае одномерного напряженного состояния

(1)

напряжение , зависящее от внешних нагрузок, при определенных условиях может

принять довольно большое значение, а предельное значение может оказаться малым, так что это неравенство нарушится. Если стечение обстоятельств, приводящее к нарушению условия прочности, редкое событие, то приходим к вероятностной трактовке условия прочности с позиций теории надежности. Вероятностью называется числовая характеристика степени возможности наступления некоторого события в определенных многократно воспроизводимых условиях. Вероятность события А можно оценить на основе опытных данных. Если проводится достаточно большое число опытов N, в которых событие Л появилось NA раз, то можно считать, что вероятность появления этого события равна

P(A)=NА/N.

Вероятность как мера возможности наступления события удовлетворяет условиям

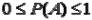, причем значение Р=0 соответствует невозможному событию, а значение Р=1 — достоверному событию.

Вероятность события, заключающегося в выполнении условия (4.1) Р(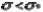) в теории надежности называется вероятностью безотказной работы. Вместо условия прочности (1) записывается условие

где Р* —заданное достаточно высокое значение вероятности, которое называется нормативной вероятностью безотказной работы. В этом случае говорят, что условие прочности обеспечено с вероятностью Р*.

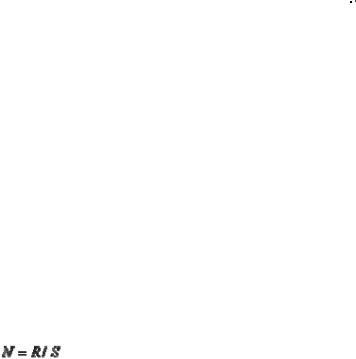
РАСЧЕТНЫЕ НАГРУЗКИ, КОЭФФИЦИЕНТЫ ЗАПАСА

Условие прочности (1) записано через напряжения, которые вычисляются через внешние нагрузки, приложенные к конструкции. Пусть внешние нагрузки определены с

точностью до одного параметра S, а напряжение связано с этим параметром зависимостью

.

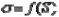Тогда условие прочности (1) можно записать через внешние нагрузки

Здесь через R обозначено предельное значение нагрузки, т.е. такое ее значение, которое приводит к предельному состоянию

.

Величина R, зависящая от свойств материала и условий нагружения, называется

несущей способностью или сопротивлением.

При заданном значении S отношение

называется коэффициентом запаса. Он обозначает, что сколько раз нужно увеличить нагрузку, чтобы достичь предельного состояния. Вместо условия прочности (2) можно записать эквивалентное условие

Если нагрузка и свойства материала являются случайными, то условия прочности (3) и (4) теряют смысл, их нужно заменить вероятностными условиями типа (2):

P(S<R)=P*,

или

P(n > 1)=P*.

При этом коэффициент запаса п также будет случайным.

Практически расчет на прочность с учетом случайного характера внешних нагрузок и случайных свойств материала проводится следующим образом. Вводится некоторое характерное значение нагрузки [S]. Это значение, называемое допускаемым или нормативным значением, можно найти из условия

где [PS] —; некоторое значение вероятности, называемое обеспеченностью. Аналогично вводится нормативное значение [R] несущей способности

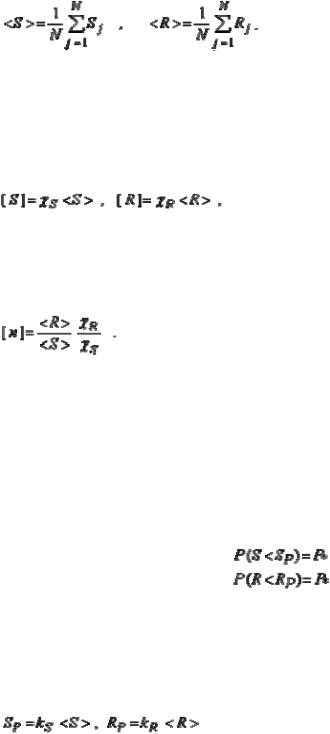
Отношение

называется нормативным коэффициентом запаса. Этот коэффициент зависит от условий нагружения, от свойств материалов, условий работы конструкции, степени ее ответственности и ряда других факторов. Такой коэффициент назначается, исходя из многолетнего опыта эксплуатации конструкций, и для каждого типа конструкций задается нормативно-технической документацией.

В качестве нормативных значений [S] и [R] можно выбрать средние значения соответствующих случайных величин

где Sj и Rj экспериментально полученные значения случайных величин в серии из N опытов. Однако в действующих нормах, в частности, строительных, нормативные значения не совпадают со средними значениями, а сдвинуты в сторону более опасных значений, что связано со значительным разбросом опытных данных около средних значений. Для нагрузки принимается несколько большее значение, а для несущей способности — меньшее

где коэффициенты 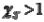и находятся из уравнений (5) и (6). Таким образом, нормативный коэффициент запаса (7) вычисляется через средние значения следующим образом:

С учетом случайного характера внешних нагрузок и сопротивлений условие прочности (3) заменяется следующим условием

SP < RP.

Здесь SР —; достаточно редко встречающееся в реальных условиях эксплуатации высокое значение нагрузки, RР —; также достаточно редко встречающееся низкое значение несущей способности. Эти значения называются расчетными. Они находятся из уравнений

(8)

(9)

В правой части уравнений содержатся нормативные значения вероятности безотказной работы, которые близки к единице (0,95; 0,99; 0,999;...).

Расчетные значения нагрузок и несущей способности можно выразить через средние значения этих величин следующим образом:

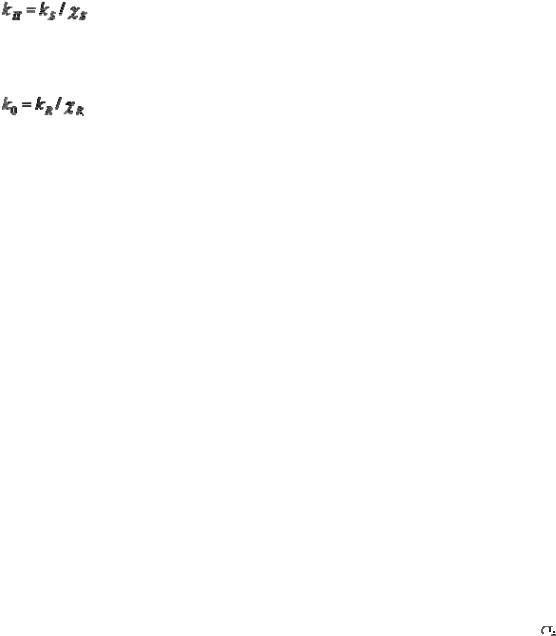
где коэффициенты kS >1 и kP < 1 находятся из решения уравнений (8) и (9). Расчетные значения связаны с соответствующими нормативными значениями соотношениями

SP = kп[S], RP = ko[R].

Коэффициент

называется коэффициентом однородности (меньше единицы). Другой коэффициент, учитывающий случайный характер несущей способности,

называется коэффициентом однородности (меньше единицы).

Это условие можно заменить равенством

SP=RP/m,

где коэффициент m >1 учитывает условия работы конструкции, степень ее ответственности. С учетом обозначения (7) для нормативного коэффициента запаса получим формулу, учитывающую случайные свойства нагрузки и несущей способности,

атакже степень ответственности конструкции

[n]= mkп / kо.

РАСЧЕТЫ ПО ДОПУСКАЕМЫМ НАГРУЗКАМ И ПО ДОПУСКАЕМЫМ НАПРЯЖЕНИЯМ

Если пренебречь случайным разбросом прочностных свойств материала конструкции, то расчетное и нормативное значения, а также среднее значение несущей способности R совпадают

RP = [R] = <R> = R,

а уравнение (7) позволяет получить выражение нормативной или допускаемой нагрузки через нормативный коэффициент запаса

[S] = R / [n].

При этом параметр несущей способности R связан с предельным значением напряжения.

Если на заданную конструкцию действует фиксированная неслучайная нагрузка S, то соотношение

NS = R / S

определяет коэффициент запаса по нагрузке. При этом условие прочности можно переписать следующим образом

S < [S].

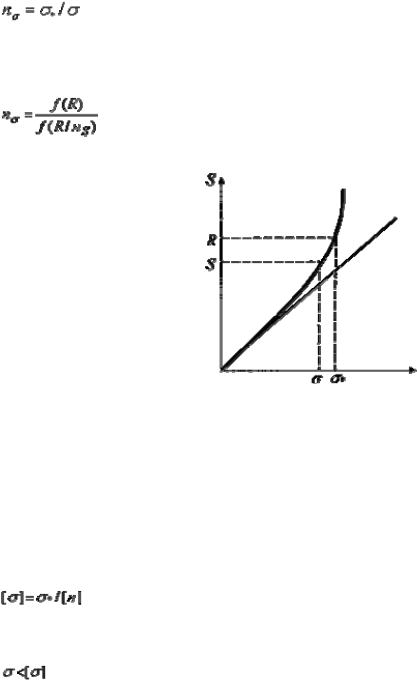
После подстановки условие прочности примет вид

nS > [n]

Переход от нагрузок к вызываемым этими нагрузками напряжениям производится по ранее описанным соотношениям. Отношение

называется коэффициентом запаса по напряжениям. С учетом (4) и (6) можно получить связь между коэффициентами запаса по нагрузкам и по напряжениям

Рис.1. Вариабельность коэффициентов запаса

Вобщем случае полученные коэффициенты запаса не совпадают, что видно из рис.

1.Равенство этих коэффициентов возможно только в том случае, когда зависимость между напряжениями и нагрузкой линейна. При нелинейной зависимости коэффициент теряет ясный физический смысл как число, на которое нужно умножить значение параметра внешней нагрузки, чтобы достичь предельного состояния. По аналогии можно ввести допускаемое напряжение

Расчет по допускаемым напряжениям

в общем случае дает результаты, отличные от расчетов по допускаемым нагрузкам. Эти результаты совпадают только в случае линейных зависимостей между напряжениями и нагрузкой.

Следует отметить, что приведенные рассуждения относятся к понятию предельного состояния в точке, которое нужно отличать от предельного состояния конструкции. Предельное состояние в точке еще не означает потерю несущей способности конструкции. Пусть предельное состояние конструкции будет достигнуто при

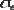
достижении параметром нагрузки S предельного значения R*. Тогда локальное условие прочности нужно заменить условием

S < R*.

Расчеты с использованием этого условия носят название расчетов по предельному состоянию для конструкции. При этом говорят о конструкционной прочности в отличие

от прочности материала, характеризуемой локальным пределом прочности или R. Конструкционная прочность зависит не только от прочностных свойств материала, но и от масштабного фактора, конструктивной формы, типа напряженного состояния, условий взаимодействия с окружающей средой и ряда других факторов.

Лекция № 12. Прочность и перемещения при центральном растяжении или сжатии

НАПРЯЖЕНИЯ ПРИ РАСТЯЖЕНИИ (СЖАТИИ) ПРИЗМАТИЧЕСКИХ СТЕРЖНЕЙ. РАСЧЕТ НА ПРОЧНОСТЬ

Переходя к изучению введенных основных видов деформации стержней, ограничимся рассмотрением стержней постоянного поперечного сечения с прямолинейной осью, т. е. призматических стержней. Начнем с деформации растяжения (сжатия).

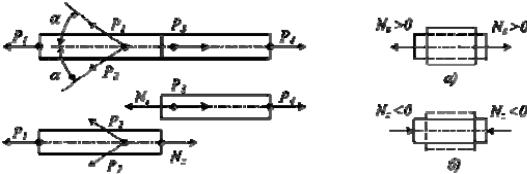
Напомним, что под растяжением (сжатием) понимают такой вид деформации стержня, при котором в его поперечном сечении возникает лишь один внутренний силовой фактор — продольная сила Nz. Поскольку продольная сила численно равна сумме проекций, приложенных к одной из отсеченных частей внешних сил на ось стержня (для прямолинейного стержня она совпадает в каждом сечении с осью Oz), то растяжение (сжатие) имеет место, если все внешние силы, действующие по одну сторону от данного поперечного сечения, сводятся к равнодействующей, направленной вдоль оси стержня (рис. 1). Одна и та же продольная сила Nz при действии на различные части стержня (левую или правую) имеет противоположные направления. Знак Nz зависит от характера вызываемой ею деформации. Продольная сила считается положительной, если вызывает растяжение элемента (рис. 2, а), и она отрицательна, если вызывает сжатие (рис. 2,б).

Для того, чтобы сформулировать предпосылки теории растяжения (сжатия) призматического стержня, обратимся к эксперименту. Представим себе стержень, изготовленный из какого-либо податливого материала (например, резины), на боковую поверхность которого нанесена система продольных и поперечных рисок (рис. 3, а). Эта ортогональная система рисок остается таковой и после приложения растягивающей нагрузки (рис. 3, б). Поскольку поперечные риски являются следами поперечных сечений на поверхности стержня и остаются прямыми и перпендикулярными к оси стержня то это свидетельствует о выполнении гипотезы плоских сечений (Бернулли). С

учетом гипотезы об отсутствии поперечного взаимодействия продольных волокон

приходим к выводу, что деформация растяжения стержня сводится к одноосному растяжению его продольных волокон, и в поперечном сечении стержня возникают лишь нормальные напряжения а (рис. 4), индекс г у которых опускаем. Ортогональность продольных и поперечных рисок свидетельствует также об отсутствии сдвигов, а, следовательно, и связанных с ними касательных напряжений т в поперечных и продольных сечениях стержня.