4. Исследование функций
Найти а) точки экстремума функции и б) точки перегиба и направления выпуклости графика функции
.Построить график функции
.
Найти точки локального экстремума
функции
и наибольшее значение этой функции на
отрезке
.Построить график функции и найти точку минимума этой функции.
Исследовать функцию
и построить ее график.Найти а) точки экстремума функции и б) точки перегиба и направления выпуклости графика функции:
.Найти а) точки экстремума функции и б) точки перегиба и направления выпуклости графика функции:
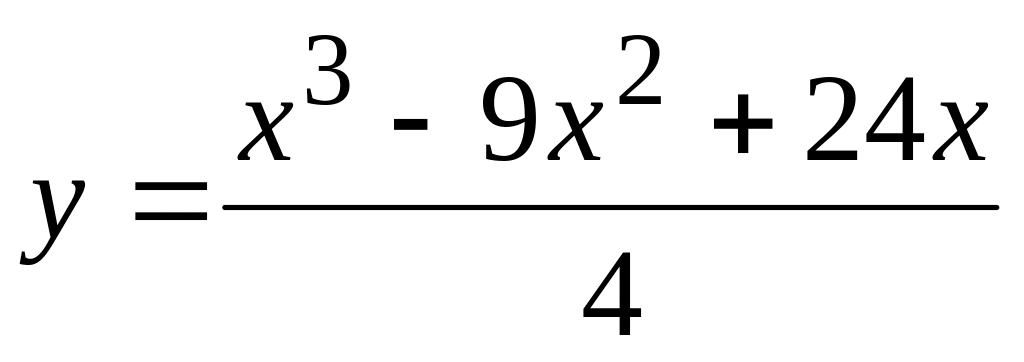.Найти а) точки экстремума функции и б) точки перегиба и направления выпуклости графика функции:
.Найти а) точки экстремума функции и б) точки перегиба и направления выпуклости графика функции:
.Приведите пример функции, не обладающей на некотором числовом промежутке наибольшим значением.
Найти асимптоты функции
.
5. Интеграл
Вычислить неопределенный интеграл, используя формулу замены переменной
.Вычислить неопределенный интеграл, используя формулу замены переменной
.Вычислить неопределенный интеграл, используя формулу замены переменной
.Используя формулу замены переменной, вычислить неопределенный интеграл
.Вычислить неопределенный интеграл, используя формулу интегрирования по частям
.Вычислить неопределенный интеграл, используя формулу интегрирования по частям
.Вычислить неопределенный интеграл, используя формулу интегрирования по частям
.Вычислить неопределенный интеграл, используя метод замены переменной
.Вычислить неопределенный интеграл
.Вычислить неопределенный интеграл
.Вычислить определенный интеграл
.Вычислить определенный интеграл
.Найти
.Вычислить определенный интеграл
.Вычислить
.Вычислить
.Вычислить
.Вычислить
.Найти
.Найти
.Найти
.Вычислить
.Вычислить неопределенный интеграл
.Приведете пример функции, которую нельзя проинтегрировать в элементарных функциях.
Вычислить площадь фигуры, ограниченной следующими линиями:
.Вычислить площадь фигуры, ограниченной следующими линиями:
.Вычислить площадь фигуры, ограниченной следующими линиями:
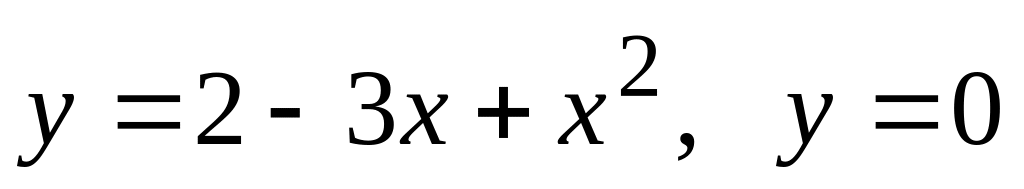.Вычислить площадь фигуры, ограниченной следующими линиями:
.Вычислить площадь фигуры, ограниченной следующими линиями:
.
КОНТРОЛЬНАЯ РАБОТА №1
Формулировки условий задач контрольной работы:
Вычислить предел функции.
Вычислить производную функции.
Исследовать функции
и
построить их графики.Вычислить неопределенные интегралы.
Вычислить площадь фигуры, ограниченной графиками функций и .
Вариант 0
1.
а)
|
б) |
в)
|
г)
|
д)
|
е)
|
2.
а)
|
б)
|
в)
|
г)
|
.3.
а)
|
б)
|
4.
а)
|
б)
|
в)
|
г)
|
5.
|
|
ВАРИАНТ 1
1.
а)
|
б)
|
в)
|
г)
|
д)
|
е)
|
2.
а)
|
б)
|
в)
|
г)
|
3.
а)
|
б)
|
4.
а)
|
б)
|
в)
|
г)
|
5.
ВАРИАНТ 2
1.
а)
|
б)
|
в)
|
г)
|
д)
|
е)
|
2.
а)
|
б)
|
в) |
г)
|
3.
а)
|
|
4.
а)
|
б)
|
в)
|
г)
|
5. 
ВАРИАНТ 3
1.
а)
|
б)
|
в)
|
г)
|
д)
|
е)
|
2.
а)
|
б)
|
в)
|
г)
|
3.
а)
|
б)
|
4.
а)
|
б)
|
в)
|
г)
|
5. 
ВАРИАНТ 4
1.
а)
|
б)
|
в)
|
г)
|
д)
|
е) |
2.
а)
|
б)
|
в)
|
г)
|
3.
а)
|
б)
|
4.
а)
|
б)
|
в)
|
г)
|
5. 
ВАРИАНТ 5
1.
а)
|
б)
|
в)
|
г)
|
д)
|
е)
|
2.
а)
|
б)
|
в)
|
г)
|
3.
а)
|
б)
|
4.
а)
|
б)
|
в)
|
г)
|
5. 
ВАРИАНТ 6
1.
а)
|
б)
|
в)
|
г)
|
д)
|
е)
|
2.
а)
|
б)
|
в)
|
г)
|
3.
а)
|
б)
|
4.
а)
|
б)
|
в)
|
г)
|
5. 
ВАРИАНТ 7
1.
а)
|
б)
|
в)
|
г)
|
д)
|
е)
|
2.
а)
|
б)
|
в)
|
г)
|
3.
а)
|
б)
|
4.
а)
|
б)
|
в)
|
г)
|
5. 
ВАРИАНТ 8
1.
а)
|
б)
|
в)
|
г)
|
д)
|
е)
|
2.
а)
|
б)
|
в)
|
г)
|
3.
а)
|
б)
|
4.
а)
|
б)
|
в)
|
г)
|
5. 
ВАРИАНТ 9
1.
а)
|
б)
|
в)
|
г)
|
д)
|
е)
|
2.
а)
|
б)
|
в)
|
г)
|
3.
а)
|
б)
|
4.
а)
|
б)
|
в)
|
г)
|
5. 
Таблицы и формулы
1. Производные основных элементарных функций
1) Производная
константы равна нулю:
.
2) 
,
где
- любое не равное нулю действительное.
В частности,
.
3) Показательная и логарифмическая функции.
|
|
|
|
4) Тригонометрические функции
|
|
|
|
5) Обратный тригонометрические функции
|
|
|
|
2. Производные некоторых сложных функций:
1.
2.
3.
4.
5.
6.
|
7.
8.
9.
10.
11.
12.
|
Правила дифференцирования
3. 
4. Константы можно
выносить за знак производной
5. Производная
суммы равна сумме производной
6. 
7. 
8. Пусть
- сложная функция,
и
Тогда:
9. Интегрирование, также как и операция дифференцирования, операция вычисления пределов, является линейной; то есть, константы можно выносить за знак интеграла, и интеграл суммы функций равен сумме интегралов. Линейность операции интегрирования можно выразить формулой:
10. Таблица основных неопределенных интегралов:
1)
2)
3)
4)
5)
6)
|
7)
8)
9)
10)
|
11)
|
|
11. Замена переменных (метод подстановки):
Если
,
то
.
Эта формула позволяет интегрировать
произведения, одним из сомножителей
которых служит сложная функция
12. Интегрирование
по частям:
13. Интегрирование простейших дробей:
1) 
2) 
3) 
14. Если
15. Формула
Ньютона-Лейбница
где
- первообразная, вычисляемая как
неопределенный интеграл с
