Лабораторная работа № 7. Поиск решения, Подбор параметра Подбор параметра

Когда желаемый результат одиночной формулы известен, но неизвестны значения, которые требуется ввести для получения этого результата, можно воспользоваться средством Подбор параметра.

При подборе параметра MS Excel изменяет значение в одной ячейке до тех пор, пока формула, зависимая от этой ячейки, не возвращает нужный результат.

Этот инструмент удобен, если нам нужно знать, на сколько изменить одну входную величину, чтобы получить желаемый результат.

Поиск решения

Поиск решения является инструментом оптимизации, с его помощью можно найти оптимальное или заданное значение некоторой ячейки путем подбора значений нескольких ячеек, удовлетворяющих нескольким граничным условиям.

Программа Поиск решения относится к надстройкам (это компоненты, установка которых позволяет дополнить Excel новыми командами и функциями) и может отсутствовать в меню. Для ее установки выполните команду Сервис→ Надстройки.... Откроется диалоговое окно, в котором установите галочку для надстройки Поиск решения и нажмите ОК. Если процесс установки завершается успешно, то в меню Сервис появляется ещё один пункт – Поиск решения.

Чтобы запустить инструмент Поиск решения выполните Сервис → Поиск решения. При этом появится диалоговое окно с установкой параметров поиска.

Ц елевая ячейка – та, для которой нужно найти максимальное, минимальное или заданное значения. Она должна содержать формулу, зависящую от изменяемых ячеек (прямо или косвенно). Пока не будет найдено решение, программа подбирает значения изменяемых ячеек.

Изменяемые ячейки – те, от которых зависит значение целевой ячейки.

Существует возможность определения результирующего значения при необходимости изменения нескольких используемых в формуле ячеек, для которых существуют несколько ограничений.

Кнопка Выполнить инициирует процесс решения. Через некоторое время в диалоговом окне появится сообщение о том, найдено решение или нет.

Цель работы: Знакомство с методами решения задач оптимизации в электронных таблицах.

Одной из задач оптимизации является задача об использовании сырья. При этом решается задача оптимизации целевой функции – критерия задачи при заданных в виде равенств и неравенств ограничений. Принятие оптимальных решений требует выполнения трех этапов:

1. анализ исходных данных;

2. создание математической модели;

3. решение задачи на компьютере;

4. анализ полученных результатов.

Рассмотрим простейшую задачу, в которой проиллюстрируем некоторые понятия задач оптимизации. Отметим, что рассматриваемая задача относится к задачам нелинейного программирования.

Задача № 1. Расчет изделия с минимальным расходом материала

Спроектировать бак, имеющий форму прямоугольного параллелепипеда, объем которого равен V = a·b·h, где a, b, h –стороны бака (длина, ширина, высота). Требуется определить размеры бака объемом V = 2000, чтобы на его изготовление пошло как можно меньше материала. Площадь материала для изготовления бака равна сумме площадей всех стенок бака и выражается формулой: S = a·b + a·b + b·h + b·h + a·h + a·h = 2(a·b + (a +b)h).

Составим математическую модель.

Очевидно, что целью задачи является экономия материала. Тогда целевая функция F зависящая от трех переменных a, b и h – это просто площадь необходимого материала S.

Необходимо найти при каких значениях a, b и h целевая функция F будет минимальной.

Итак, задача может быть записана в форме математической модели:

F = S → min

V = 2000.

Эта запись читается так:

минимизировать величину S при условии, что V = 2000. Подставив значения F и S, получим: F=2·(a·b + (a + b)·h) → min, а т.к. V=a·b·h, то a·b·h = 2000

И, наконец, нужно добавить ограничения (граничные условия) на параметры бака: а > 0, b > 0, h > 0.

Составим таблицу для решения задачи и решим ее средствами Excel.

♠ Будьте внимательны: имена столбцов набираются латинскими буквами!

Ввод данных

Введите текст:	в ячейку А1 – Целевая функция F;
	в ячейку А3 – Расчетные показатели;
	в ячейки А4:А7 – a=, b=, h=, V=.

Ячейки D1, D2, D3 будем использовать для ввода начальных значений переменных a, b и h, для дальнейшего поиска оптимального решения. Пока будем считать их равными нулю.

В ячейку B1 введем для целевой функции F формулу, которая будет иметь следующий вид =2*(D1*D2+(D1+D2)*D3)

В ячейки B4, B5 и B6 последовательно введем формулу со ссылкой на ячейки D1, D2, D3 (в B4 =D1, в B5 =D2 и в B6 =D3), для дальнейшего ввода ограничений на параметры бака.

В ячейку B7 введите формулу =D1*D2*D3 для расчета объема бака, т.е. ограничения по объему, который должен быть равен 2000.

Приступим к поиску решения задачи.

Выберите команду Сервис–Поиск решения. Появится окно диалога «Поиск решения» – рис. 1.

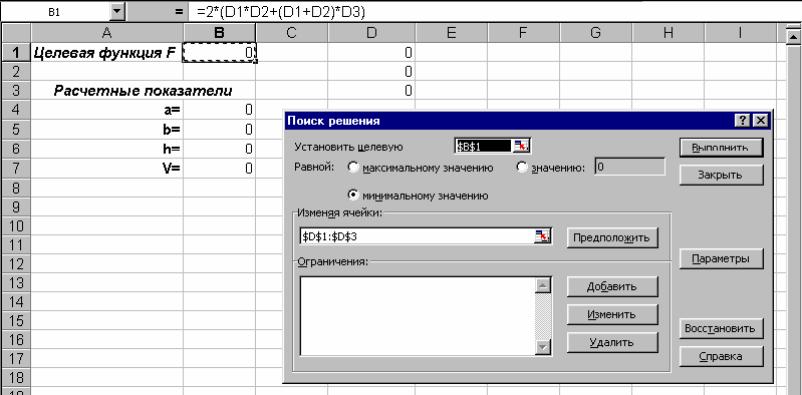
Рис. 1 Окно диалога «Поиск решения». Указатель находится в ячейке В1.

Так как формула для целевой функции находится в ячейке B1, то нужно щелкнуть мышью на этой ячейке. В поле окна диалога «Установить целевую ячейку» появится автоматически абсолютная ссылка $B$1. (Примечание: можно набрать значение абсолютной ссылки с клавиатуры, но щелкнуть мышью проще!).

В поле «Изменяя ячейки» укажите ссылку на диапазон ячеек D1:D3.

Установите переключатель «Минимальное значение».

Теперь необходимо ввести ограничение для поиска решения. Нажмите кнопку Добавить, чтобы ввести информацию в поле Ограничения – рис. 2.

Рис. 2 Окно диалога «Добавить ограничения»

В поле Ссылка на ячейку введите B4. В списке неравенств выберите >= – больше или равно. В поле Ограничение введите число 0.

Нажмите кнопку Добавить.

Введите аналогичные ограничения для ячеек B5 и B6. Введите ограничение для ячейки B7: =2000. После ввода последнего ограничения нажмите клавишу Enter или кнопку OK.

Окно диалога «Поиск решения» примет следующий вид – рис. 3.

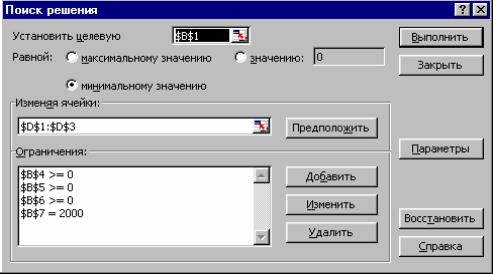
Рис. 3 Окно диалога «Поиск решения» после ввода ограничений

Решение задачи

Теперь все параметры для поиска решения введены и, можно дать команду к выполнению поиска решения. Нажмите кнопку Выполнить. В окне Результаты поиска решения выведено сообщение «Поиск не может найти подходящего решения», т.к. в ячейках D1, D2, D3 были заданы нулевые начальные значения (рис. 4).

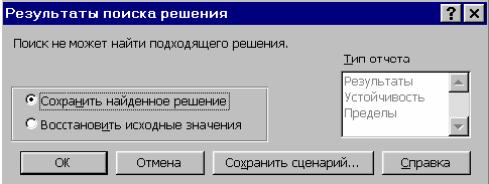
Рис. 4 Окно Результаты поиска решения (при нулевых начальных данных!)

При решении задач линейного программирования достаточно часто не удается получить оптимального решения. Это происходит по следующим причинам:

• Неправильная математическая модель или неправильные исходные данные.

• Неограниченность целевой функции. При максимизации целевая функция должна быть

ограничена сверху, при минимизации – снизу.

Измените начальные условия в ячейках D1:D3 на 1. Снова выберите команду Сервис – Поиск решения и нажмите кнопку Выполнить. Теперь в окне поиска решения появилось сообщение: «Решение найдено. Все ограничения и условия оптимальности выполнены». (Примечание: если в эти ячейки ввести отрицательные числа, то согласно заданным ограничениям, решение все равно будет найдено).

Рис. 5 Окно Результаты поиска решения (при ненулевых начальных данных!)

Чтобы получить отчет по найденному решению в окне Результаты поиска решения выберите Тип отчета: Результаты, нажав кнопку OK, получите лист с отчетом по результатам поиска решения. Перед тем листом, где записана постановка задачи автоматически будет вставлен лист Отчет по результатам 1. В этом отчете содержится ответ на поставленную задачу.

Искомый параллелепипед оказался кубом со сторонами ≈ 12,6.

Переименуйте рабочий лист и дайте ему название Бак.

Задача № 2. План выгодного производства

Условие задачи: Предположим, что мы решили производить несколько видов конфет. Назовем их условно "A", "B" и "C".

Конфеты можно производить в любых количествах (сбыт обеспечен), но запасы сырья ограничены.

Известно, что реализация 10-ти килограмм конфет "А" дает прибыль 9 р., "В" – 10 р. и "С" – 16 р.

Надо определить, каких конфет и сколько десятков килограмм необходимо произвести, чтобы общая прибыль от реализации была максимальной.

Решение задачи: Перейдем на другой лист рабочей книги, переименуйте его Конфеты, создайте таблицу с данными норм расхода сырья как показано на рис. 6. (ячейки B6, C6, D6 имеют формат Денежный).

Рис. 6. Таблица с данными норм расхода сырья.

Создайте и введите формулы в таблицы для нахождения решения поставленной задачи, как указано на рис 7.

Примечание: Количество конфет будет измеряться в десятках килограмм, т.к. нормы расхода сырья и получаемая от этого прибыль тоже приведены из расчета на 10 кг конфет.

Рис. 7. Таблицы с формулами для Поиска решения максимальной прибыли

Обратите внимание, что в ячейках А17, В17, С17 находится формула, отражающая сумму расхода сырья на производство каждого вида конфет, при этом каждая из них имеет ограничение по количеству имеющегося сырья. В меню Сервис активизируйте команду Поиск решения и опишите его ограничения, как показано на рис 8.

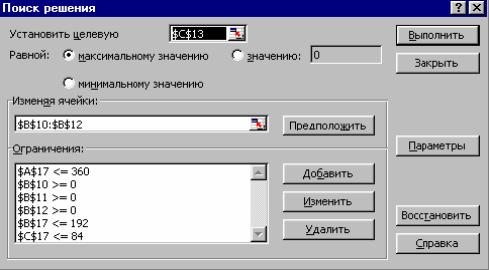
Рис. 8. Вид окна Поиск решения с заданными ограничениями.

Если Вы сделали все верно, то решение будет таким, как на рис 9.

Рис. 9. Вид рабочего листа "Конфеты" после нахождения решения

Вывод: Из решения видно, что оптимальный план выпуска предусматривает изготовление 80 кг конфет "В" и 200 кг конфет "С". Конфеты "А" производить не стоит. Полученная Вами прибыль составит 400 р. При этом сырье израсходуется полностью, кроме наполнителя, расход которого составит 84 кг из имевшихся 180 кг.

Задача № 3. Транспортная задача

В пунктах A и B находятся соответственно 150 и 190 т горючего. Пунктам 1, 2, 3 требуются соответственно 160, 70, 110 т. горючего. Стоимость перевозки 1 т горючего из пункта A в пункты 1, 2, 3 равна 60, 10, 40 тыс. руб. за 1 т соответственно, а из пункта B в пункты 1, 2, 3 – 120, 20, 80 тыс. руб. за 1 т соответственно. Составьте план перевозок горючего, минимизирующий общую сумму транспортных расходов.

Технология работы:

1. Исходные данные задачи представлены в табл. 1.

Таблица 1

Исходные данные

Поставщики	Потребители			Запасы
	1	2	3
A	60	10	40	150
B	120	20	80	190
Потребность	160	70	110

Важно отметить, что данная задача должна быть сбалансирована, то есть запасы горючего и потребность в нем равны (т.е. 160+70+110=150+190). В этом случае не нужно учитывать издержки, связанные как со складированием, так и с недопоставками. В противном случае в модель нужно ввести:

• в случае превышения объема запасов – фиктивного потребителя; стоимость перевозок единицы продукции этому фиктивному потребителю полагается равной стоимости складирования, а объемы перевозок этому потребителю равны объемам складирования излишек продукции у поставщиков;

• в случае дефицита – фиктивного поставщика; стоимость перевозок единицы продукции от фиктивного поставщика полагается равной стоимости штрафов за недопоставку продукции, а объемы перевозок от этого поставщика равны объемам недопоставок продукции потребителям.

2. Теоретические сведения.

Для решения данной задачи построим ее математическую модель. Неизвестными здесь являются объемы перевозок. Пусть x_ij – объем перевозок от i-того поставщика j-тому потребителю. Функцией цели являются суммарные транспортные расходы, т.е.

,

где c_ij – стоимость перевозки единицы продукции от i-того поставщика j-тому потребителю. Кроме того, неизвестные должны удовлетворять следующим ограничениям:

• неотрицательность объема перевозок;

• в силу сбалансированности задачи, вся продукция должна быть вывезена от поставщиков и потребности всех потребителей должны быть удовлетворены.

Таким образом, мы имеем следующую модель:

,

где a_i – запасы горючего у i- того поставщика; b_j – спрос у j-того потребителя.