3. Переведення чисел з двійкової, вісімкової та шістнадцяткової систем числення у десяткову.

Для переведення чисел з двійкової, вісімкової та шістнадцяткової системи числення у десяткову використовують формулу:

(a_na_n-1a_n-2...a₀a_-1a_-2...)_p=a_npⁿ+a_n-1p^n-1+a_n-2p^n-2+...+a₀p⁰+a_-1p^-1+a_-2p^-2+...

де a_n, a_n-1, a_n-2, ... a₀, a_-1, a_-2, ... – цифри у числі;

n, n-1, n-2, ..., 0, -1, -2, ... – позиція цифри у числі;

р – основа системи числення.

Приклад. Перевести числа (276)₈, (100101,01)₂ та (3F)₁₆ у десяткову систему числення.

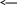_{2 1 0}

(276)₈=2*8²+7*8¹+6*8⁰=128+56+6=(190)₁₀

_{5 4 3 2 1 0 -1 -2}

(100101,01)₂=1*2⁵+1*2²+1*2⁰+1*2^-2=32+4+1+1/4=(37,25)₁₀.

4. Переведення чисел з двійкової, вісімкової та шістнадцяткової систем числення у десяткову.

Для переведення чисел з однієї системи числення в іншу (крім десяткової) використовують декілька способів.

1. Щоб перевести число з двійкової системи числення в вісімкову або шістнадцяткову, з вісімкової в двійкові та шістнадцяткову, з шістнадцяткової в двійкову та вісімкову систему необхідно спочатку перевести дане число в десяткову систему. Після чого з десяткової системи числення перевести у необхідну систему.

2. Цифри вісімкової системи замінюються на двійкові згідно з таблицею 1.

Таблиця 1

Вісімкові цифри	0	1	2	3		4		5	6	7
Двійкові числа	000	001	010		011		100	101	110	111

Використовуючи таблицю 1 можна записати правило переведення цілих двійкових чисел у вісімкові:

 розбити запис двійкового числа справа наліво по 3 цифри;

 доповнити зліва нулями до 3 цифр крайній лівий запис;

 кожну групу з 3 двійкових цифр замінити відповідною вісімковою цифрою згідно таблиці 1.

Приклад. Перевести у вісімкову систему двійкове число (1011101)₂.

(1011101)₂=(001 011 101)₂=(135)₈.

^{1 3 5}

3. Цифри шістнадцяткової системи змінюються на двійкові числа згідно з таблицею 2.

Таблиця 2

Шістнадцяткові	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
Двійкові	0000	0001	0010	0011	0100	0101	0110	0111	1000	1001	1010	1011	1100	1101	1110	1111

Використовуючи таблицю 2 можна записати правило переведення цілих двійкових чисел в шістнадцяткові:

 розбити запис двійкового числа справа наліво по 4 цифри;

 доповнити зліва нулями до 4 цифр крайній лівий запис;

 кожну групу з 4 двійкових цифр замінити відповідною шістнадцятковою цифрою.

Приклад. Перевести у шістнадцяткову систему двійкове число (1011101)₂

(1011101)₂=(0101 1101)₂=(5D)₁₆

^{5 D}

Зведемо в таблицю 3 співвідношення чисел з різними основами.

Таблиця 3.

10-кові	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
2-кові	0	1	10	11	100	101	110	111	1000	1001	1010	1011	1100	1101	1110	1111
8-кові	0	1	2	3	4	5	6	7	10	11	12	13	14	15	16	17
16-кові	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F

Якщо є необхідність перевести вісімкове ціле число в шістнадцяткове, використовують таку послідовність дій:

 перевести вісімкове число в двійкове;

 Розбити запис двійкового числа справа наліво по 4 цифри;

 доповнити зліва нулями до 4 цифр крайній лівий запис;

 кожну групу з 4 двійкових цифр замінити відповідною шістнадцятковою цифрою.

Приклад. Перевести вісімкове число (231)₈ в шістнадцяткову систему.

1. (231)₈=(010 011 001)₂

^{2 3 1}

2. (1001,1001)₂=1001,1001=(99)₁₆

^{9 9}

При переведенні двійкового дробу у вісімковий або шістнадцятковий використовують тіж способи, що і для переведення цілих чисел. Але розбивка двійкового дробу здійснюється зліва від коми направо по 3 цифри (для вісімкової системи) і по 4 цифри (для шістнадцяткової).

Приклад. Перевести двійкове число (0,1010111)₂ в вісімкову та шістнадцяткову системи.

(0,1010111)₂=(0,101 011 100)₂=(0,534)₈

^{5 3 4}

(0,1010111)₂=(0,1010 1110)₂=(AE)₁₆

^{A E}