2. Для интерполяционного метода

Алгоритм:

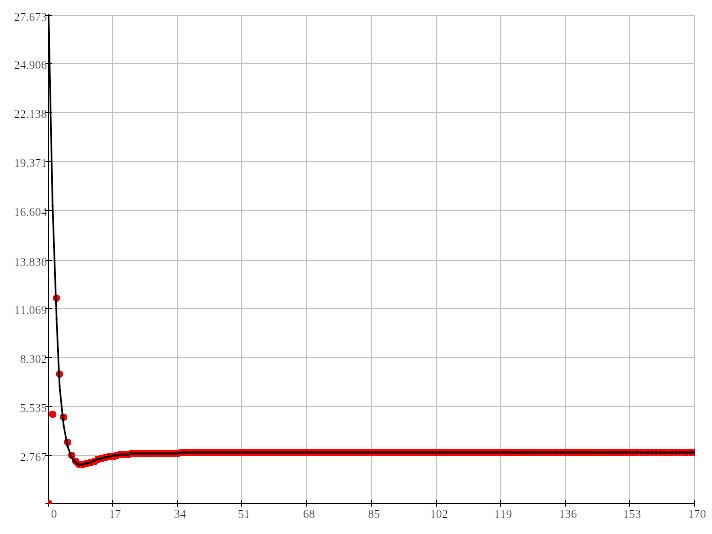Рисунок 4.17: Переходные процессы в аналоговом и цифровом ( ) фильтрах для интерполяционного метода.

Посчитаем среднеквадратичное отклонени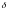е переходного процесса в цифровом фильтре от переходного процесса в аналоговом фильтре:

. Здесь:

— функция выхода аналогового фильтра, определённая выражением (3.26),

— её устоявшееся (достигнутое к десятой секунде) значение,

— n-ый отсчёт функции выхода цифрового фильтра, определённой страницу назад сформированным алгоритмом.

Алгоритм оправдал наши ожидания: построенный по нему цифровой фильтр достаточно точно повторил свой аналоговый прототип.

3. Для экстраполяционного метода

Алгоритм:

Рисунок 4.18: Переходные процессы в аналоговом и цифровом ( ) фильтрах для экстраполяционного метода.

Посчитаем среднеквадратичное отклонение переходного процесса в цифровом фильтре от переходного процесса в аналоговом фильтре:

Алгоритм оправдал наши ожидания: построенный по нему цифровой фильтр достаточно точно повторил свой аналоговый прототип.

2. Замкнутая система с цифровым фильтром

Для формирования алгоритма моделирования замкнутой системы с цифровым фильтром, рассмотрим временную диаграмму:

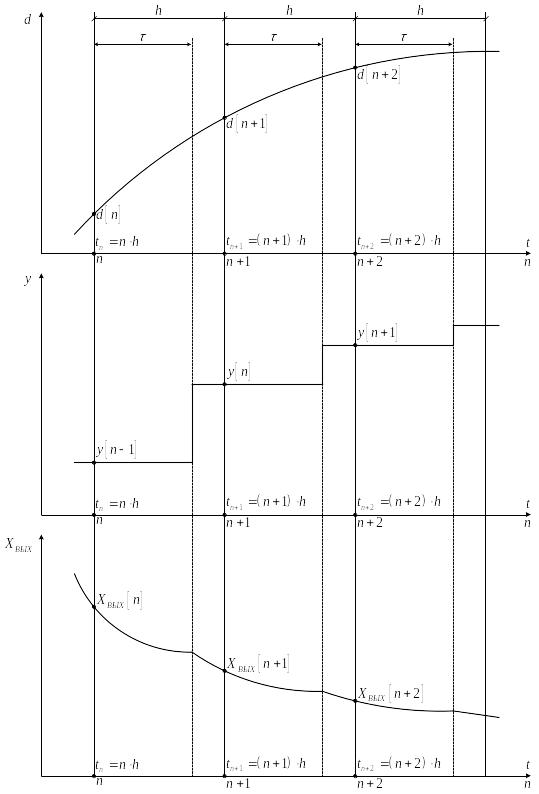
Рисунок 4.19: Временная диаграмма цифрового фильтра в составе замкнутой системы.

Рассмотрим момент времени . В этот момент АЦП измеряет входной сигнал . В памяти ЦВМ при этом хранятся значения и , а так же вычисленные на прошлом шаге промежуточные величины и . По этим параметрам (с учётом только что снятых с АЦП показаний) ЦВМ вычисляет значение в соответствии с алгоритмом, описанном в предыдущем пункте. Но выставлено на ЦАП оно будет лишь в момент времени , где , — запаздывание, — складывается из чистого запаздывания (время срабатывания АЦП и ЦАП и время собственно вычисления) и введённого при необходимости искусственного запаздывания.

При отсутствии помех ( ), уравнение объекта в произвольный момент времени имеет вид:

. (4.15)

На интервале времени от до величина постоянна и равна , и с помощью формул Тейлора мы получаем:

(4.16)

На интервале времени от до величина так же постоянна, но равна уже , тогда с помощью (4.16) мы вычисляем значения следующего отсчёта:

(4.17)

Для завершения построения модели осталось добавить к полученным уравнениям ещё одно, уравнение обратной связи:

. (4.18)

3. Выбор шага дискретизации

С помощью модели, полученной в предыдущем пункте, построим график переходного процесса в замкнутой системе с цифровым фильтром в сравнении с графиком переходного процесса в замкнутой системе с аналоговым фильтром при отсутствии внешнего возмущения ( ) и запаздывания в цифровом фильтре ( ) при различных шагах дискретизации. На вход системы подадим единичное ступенчатое воздействие ( при ). Построение будем вести на интервале времени от 0 до 0.6 (которому соответствует интервал отсчётов от 0 до ), к концу которого переходный процесс гарантированно закончится. Для каждого построенного переходного процесса в замкнутой системе с цифровым фильтром определим:

• Среднеквадратичное отклонение от переходного процесса в замкнутой системе с аналоговым фильтром по формуле:

, где: (4.19)

— функция выхода замкнутой системы с аналоговым фильтром, определённая выражением (3.16),

— её устоявшееся (достигнутое к десятой секунде) значение,

— n-ый отсчёт функции выхода замкнутой системы с цифровым фильтром, определённой моделью, построенной в предыдущем пункте.

• Перерегулирование , как:

. (4.20)

• Время переходного процесса , как момент вхождения переходного процесса в пятипроцентный -коридор своего устоявшегося значения.

При построениях:

С плошной линией будем обозначать график переходного процесса в замкнутой системе с аналоговым фильтром.

Жирными точками — график переходного процесса в замкнутой системе с цифровым фильтром, работающем по полуаналитическому интерполяционному методу

Жирными треугольниками — график переходного процесса в замкнутой системе с цифровым фильтром, работающем по полуаналитическому экстраполяционному методу

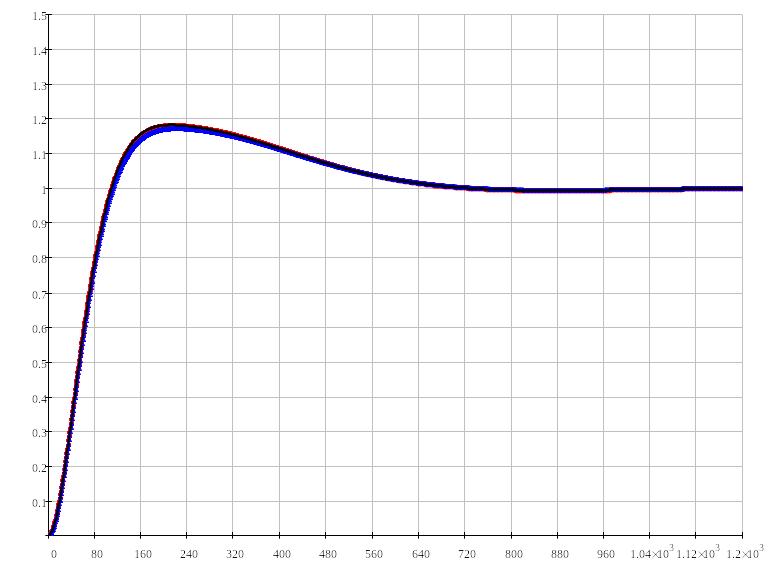
Рисунок 4.20: Переходный процесс в замкнутой системе при , .

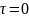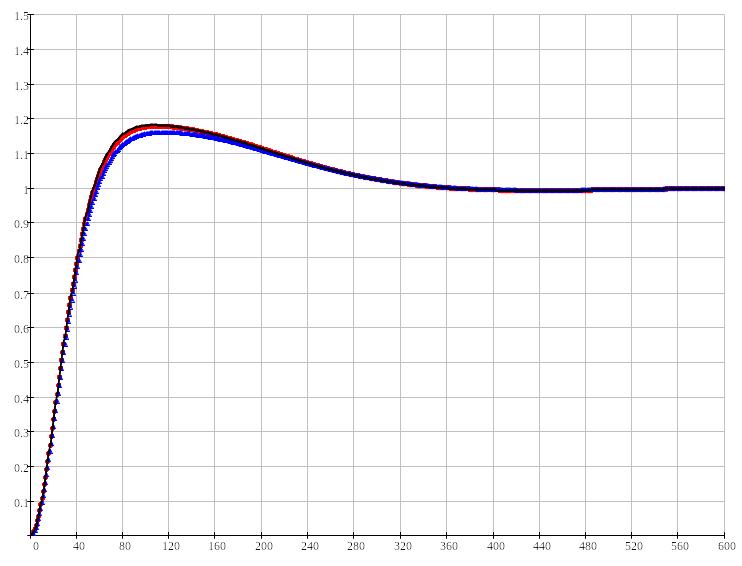
Рисунок 4.21: Переходный процесс в замкнутой системе при , .

Рисунок 4.22: Переходный процесс в замкнутой системе при , .

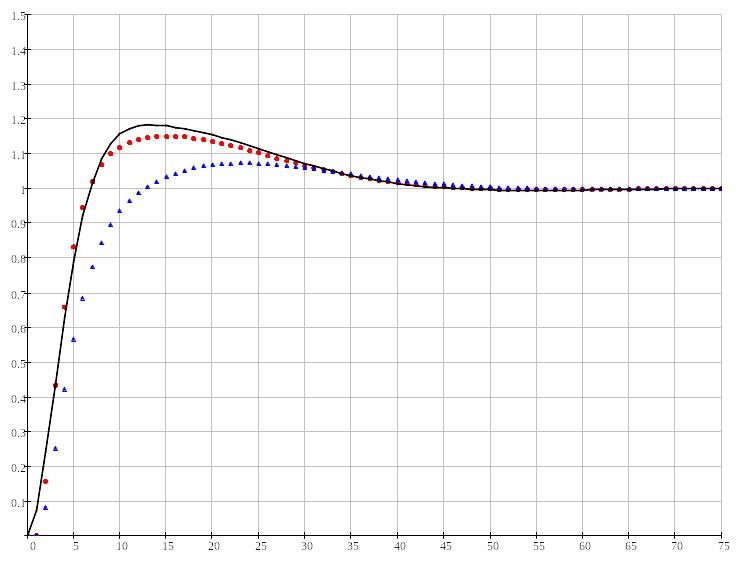
Рисунок 4.23: Переходный процесс в замкнутой системе при , .

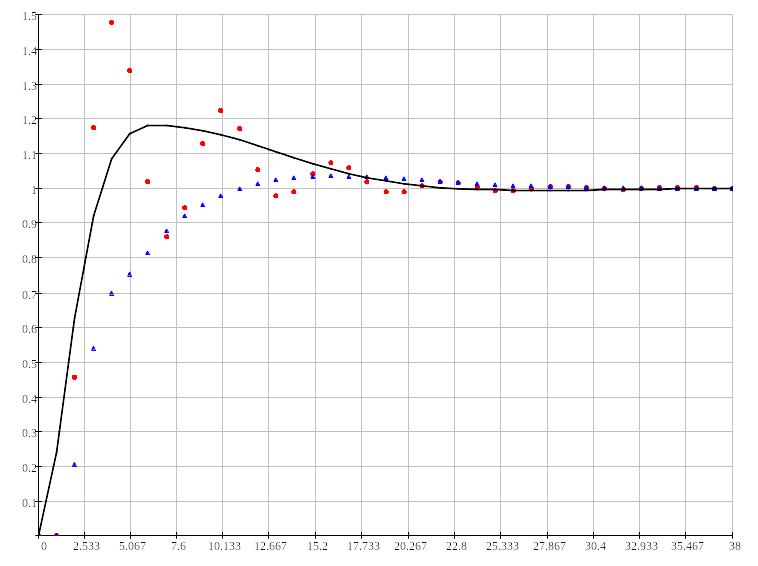
Рисунок 4.24: Переходный процесс в замкнутой системе при , .

Занесем результаты в таблицу:

Метод	▲ Интерполяционный					● Экстерполяционный
	0.0005	0.001	0.004	0.008	0.016		0.0005	0.001	0.004	0.008	0.016
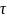
	0	0	0	0	0		0	0	0	0	0
	0.660	1.310	4.993	9.422	16.826		0.139	0.264	0.821	1.196	Неустойчива
	0.171	0.161	0.112	0.072	0.0344		0.180	0.178	0.166	0.148
	0.264	0.264	0.246	0.264	0.144		0.263	0.264	0.268	0.264

Таблица 4.2: Характеристики переходного процесса при различных значениях .

Выберем следующие значения исходя из условия :

Интерполяционный метод: , при этом

Экстерполяционный метод: , при этом