2 Анализ и уточнение требований к программному продукту

2.1 Анализ процесса обработки информации и описание структур данных для ее хранения

2.1.1 Диаграмма вариантов использования

Диаграмма вариантов использования – это визуальная модель, отражающая спецификацию ПС с точки зрения её функциональности. На рисунке 1 представлена в виде диаграммы вариантов использования функциональность разрабатываемого в данной работе программного средства.

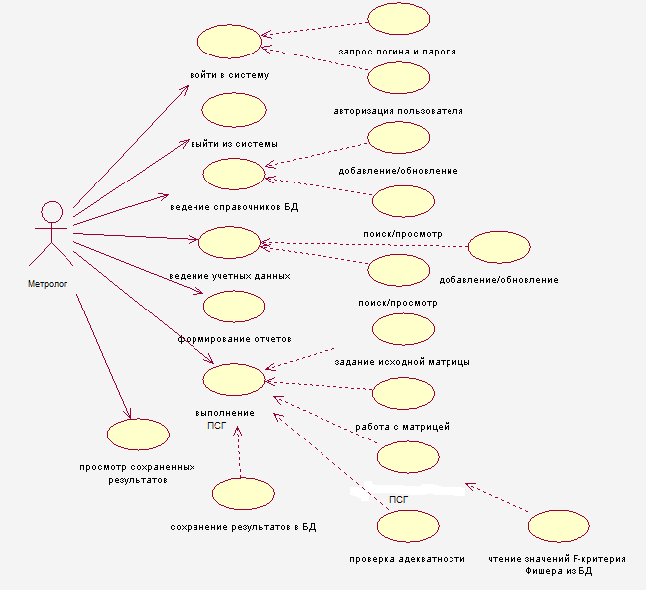
Рисунок 1

2.1.2 Даталогическая модель бд

Информация, используемая в качестве входных данных для программного средства, хранится в базе данных «Приборы.mdb». Структура базы данных представлена в виде даталогической модели (ДЛМ) на рисунке 2.

Для построения даталогической модели используются модели на основе физических записей. Существуют иерархические, сетевые, реляционные модели данных /2/. В данной работе использована реляционная модель данных.

Реляционное отношение (таблица) – это подмножество декартового произведения k доменов, имеющих смысл с точки зрения рассматриваемой предметной области. Домен – это допустимое множество значений одного типа.

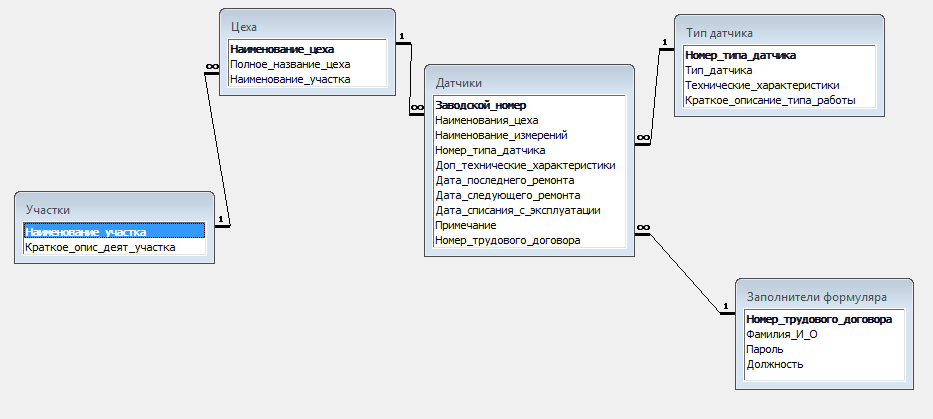
Рисунок 2 – Иерархия функций

2.2 Выбор методов и разработка основных алгоритмов решения задачи

Для разработки приложений АИС используются следующие методы:

проверка статистических гипотез;
корреляционно-регрессионный анализ;
кластерный анализ;
дискриминантный анализ;
факторный анализ.

В качестве метода решения прогнозирования был выбран метод проверки статистических гипотез.

Статистические гипотезы – это выдвигаемые теоретические предположения относительно параметров статистического распределения или закона распределения случайной величины. В соответствии с решаемой задачей различают параметрические и непараметрические гипотезы.

При проверке статистических гипотез используются понятия нулевой (прямой) и альтернативной (обратной) гипотез. Прямая гипотеза ( ) является основной и обычно содержит утверждение об отсутствии различий между сравниваемыми величинами. Альтернативная величина ( ) принимается после того, как отвергнута основная.

В статистике рассматривают простые и сложные параметрические гипотезы. Простая гипотеза содержит только одно предположение относительно оцениваемого параметра. Сложная гипотеза состоит из нескольких простых гипотез.

Для того чтобы проверить гипотезу, используют статистические критерии, позволяющие выяснить, следует ли принять или опровергнуть нулевую гипотезу. Если расчетное значение критерия не превышает критического, то есть веские основания для принятия прямой (нулевой) гипотезы. В противоположном случае целесообразно предположить справедливость альтернативной гипотезы ( ).

Проверка статистических гипотез всегда допускает определенную вероятность ошибки в выводах:

- вероятность отвергнуть нулевую гипотезу, когда она справедлива;

- вероятность принять нулевую гипотезу, когда она ложна.

В исследованиях обычно используется - вероятность ошибки первого рода. Наиболее распространенными в практике экономического анализа значениями являются: 0,01; 0,05; 0,1.

В многомерном анализе для проверки статистических гипотез используются те же статистические критерии, что и в одномерном, но они изменяются с учетом природы многомерных случайных величин. Чаще всего это критерии для проверки параметрических гипотез: t-Стьюдента, F-Фишера, и проверки непараметрических гипотез - .

В многомерном статистическом анализе проверка гипотезы о равенстве вектора средних значений заданному вектору основывается на тех же подходах, что и для одномерных величин. Но в этом случае имеет место -чисел выборочных средних значений: