Тема «Линейные пространства и их преобразования» Вариант 1.
Найти координаты вектора
в базисе
,
,
,
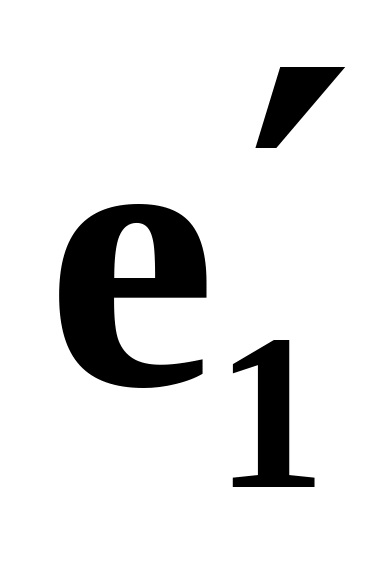если он задан в базисе
,
,
:
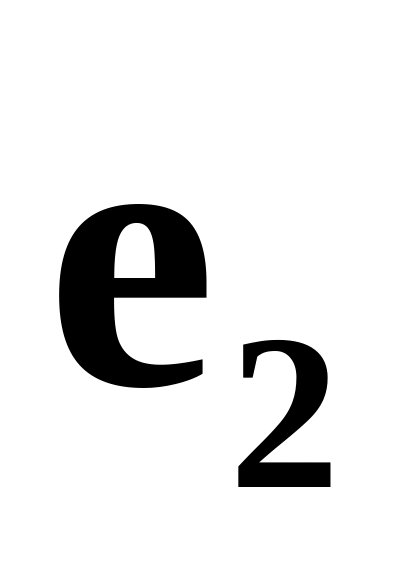и
,
,
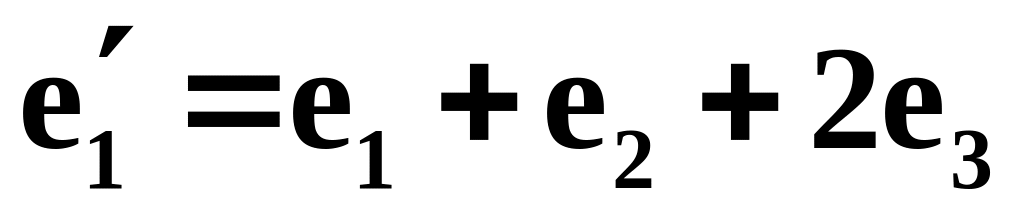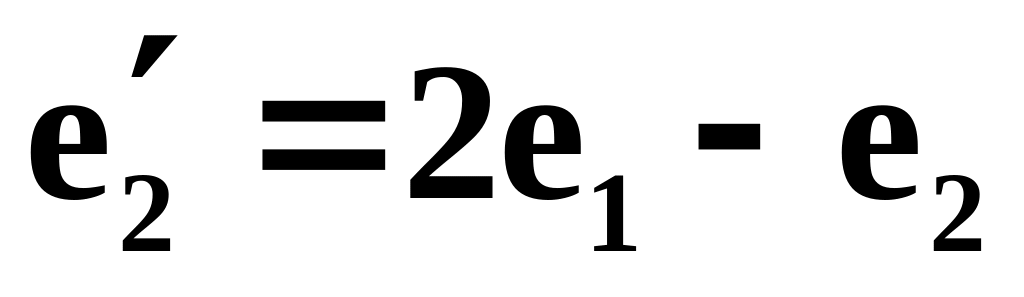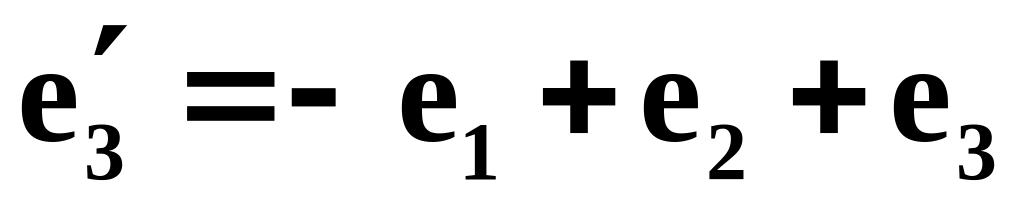.Найти фундаментальную систему решений и общее решение однородной системы линейных уравнений
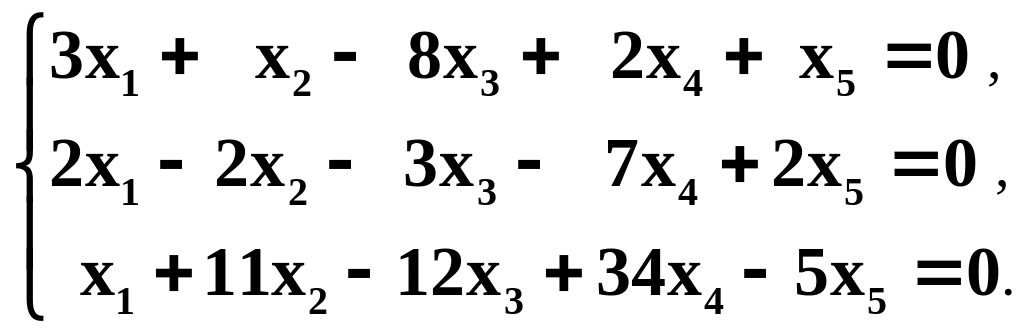
Являются ли линейными преобразованиями отображения
:
Пусть
,
– линейные преобразования пространства
в себя:
где
– произвольный элемент
.
Найти
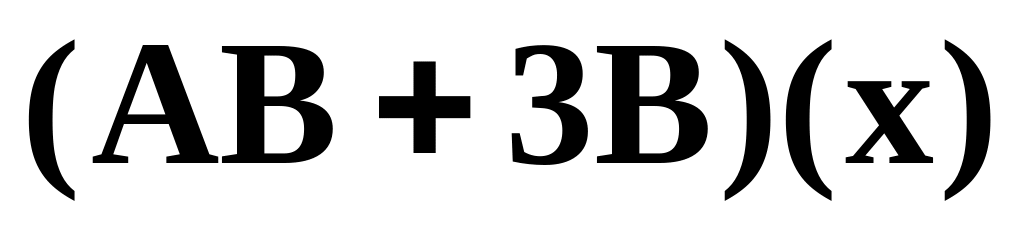.Линейное преобразование в базисе , , задано матрицей
.
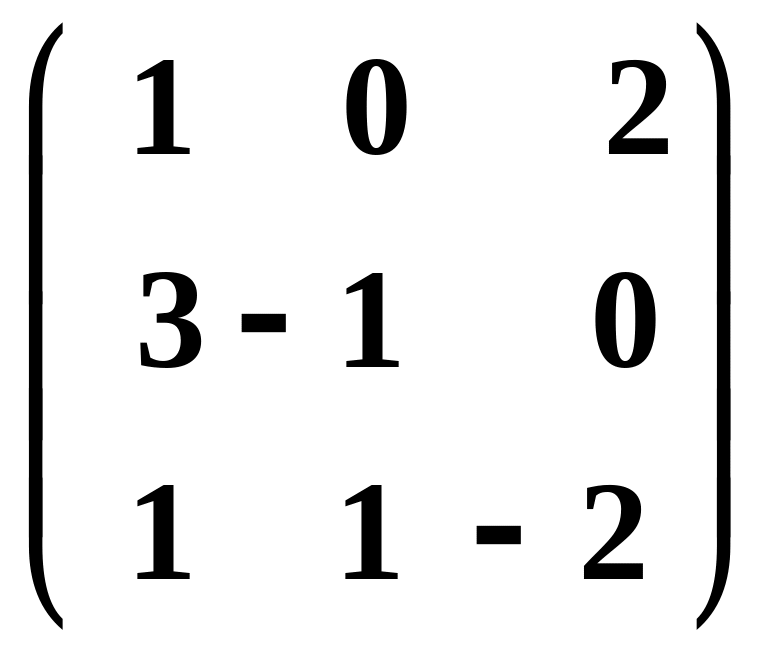Найти его матрицу в базисе
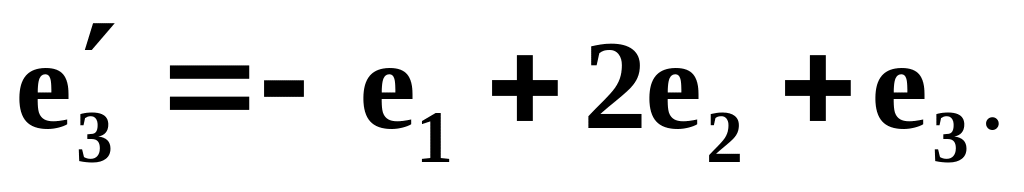
Найти собственные значения и собственные вектора линейного преобразования, заданного в некотором базисе матрицей
.
Тема «Линейные пространства и их преобразования»
Вариант 2.
Найти координаты вектора в базисе , , , если он задан в базисе , , :
и
,
,
.
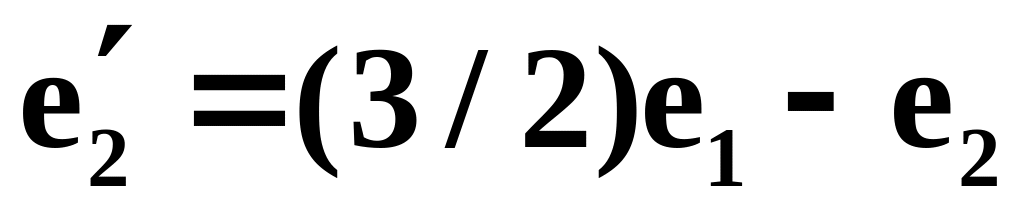Найти фундаментальную систему решений и общее решение однородной системы линейных уравнений
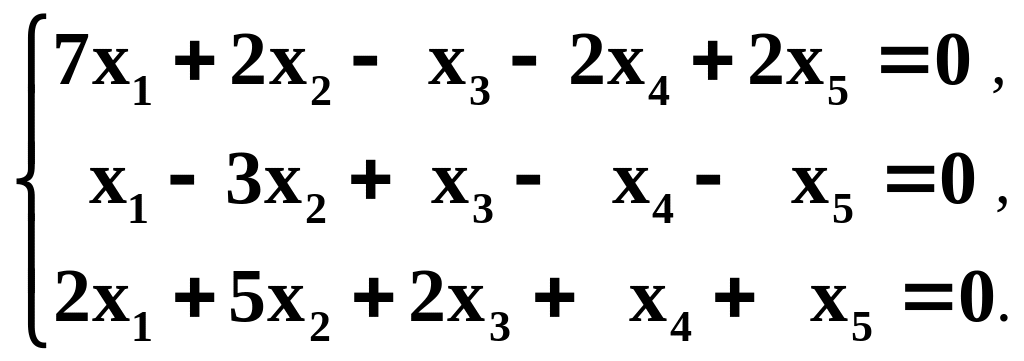
Являются ли линейными преобразованиями отображения :
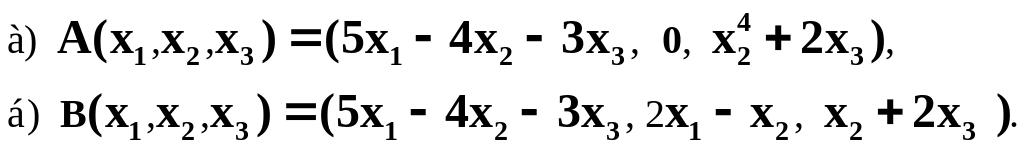
Пусть , – линейные преобразования пространства в себя:
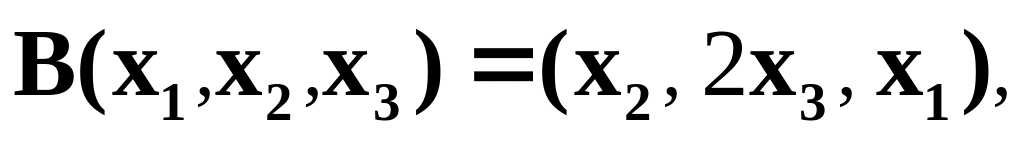где
– произвольный элемент
.
Найти
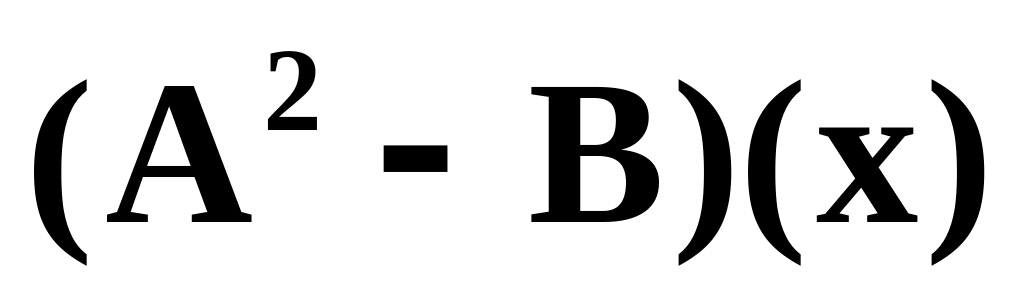.Линейное преобразование в базисе , , задано матрицей
.
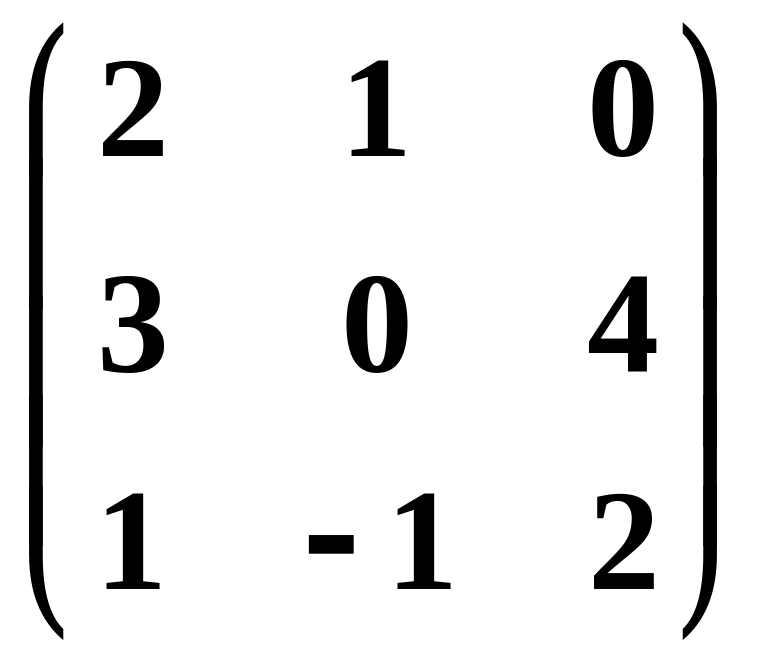Найти его матрицу в базисе
Найти собственные значения и собственные вектора линейного преобразования, заданного в некотором базисе матрицей
.
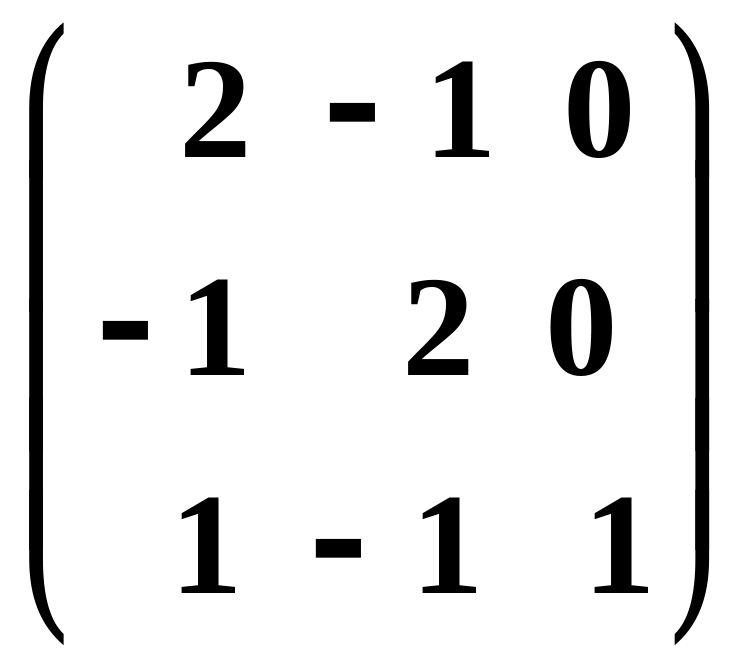Тема «Линейные пространства и их преобразования» Вариант 3.
Найти координаты вектора в базисе , , , если он задан в базисе , , :
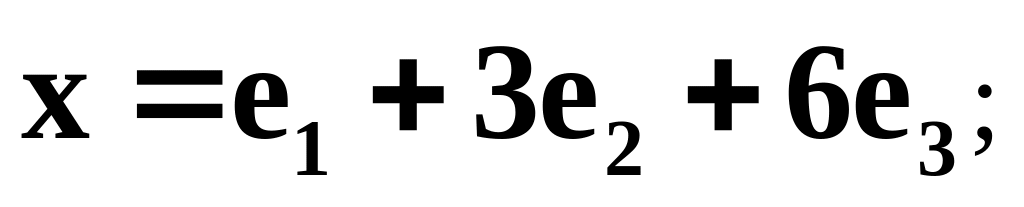
Найти фундаментальную систему решений и общее решение однородной системы линейных уравнений
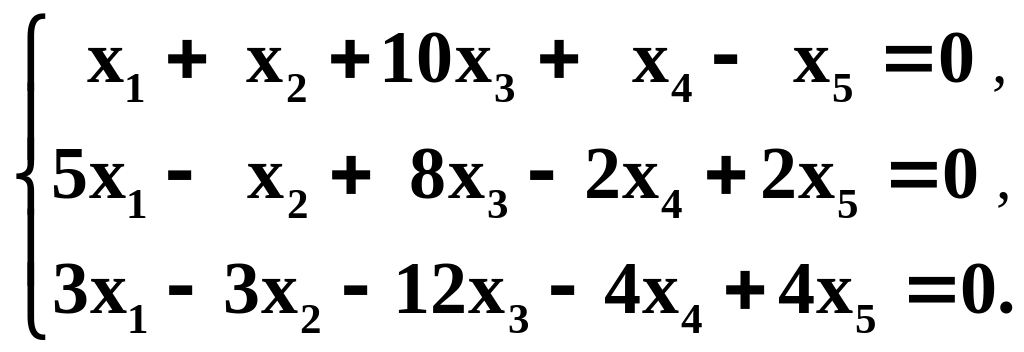
Являются ли линейными преобразования отображения :
Пусть , – линейные преобразования пространства в себя: где – произвольный элемент . Найти
.Линейное преобразование в базисе , , задано матрицей
.
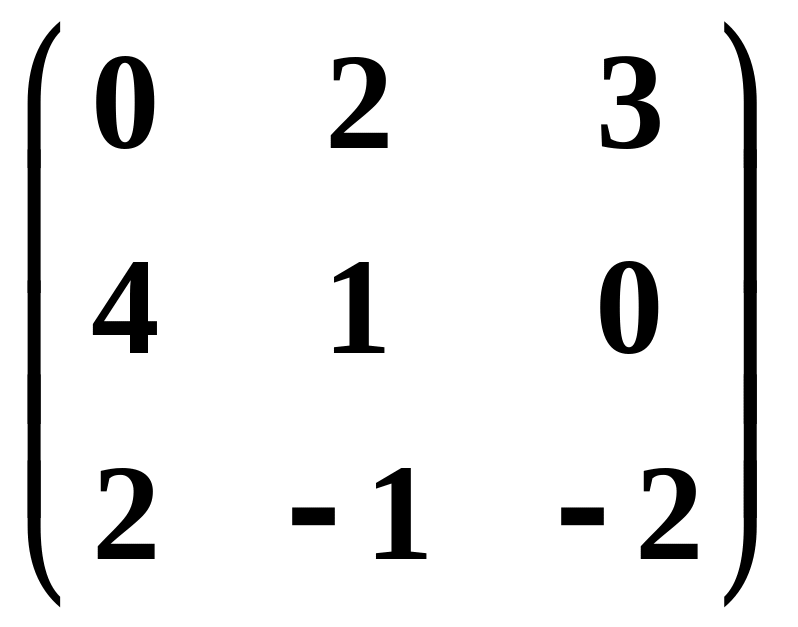Найти его матрицу в базисе
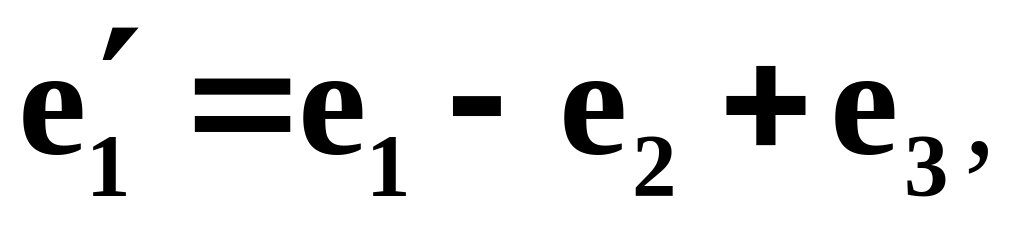
Найти собственные значения и собственные вектора линейного преобразования, заданного в некотором базисе матрицей
.
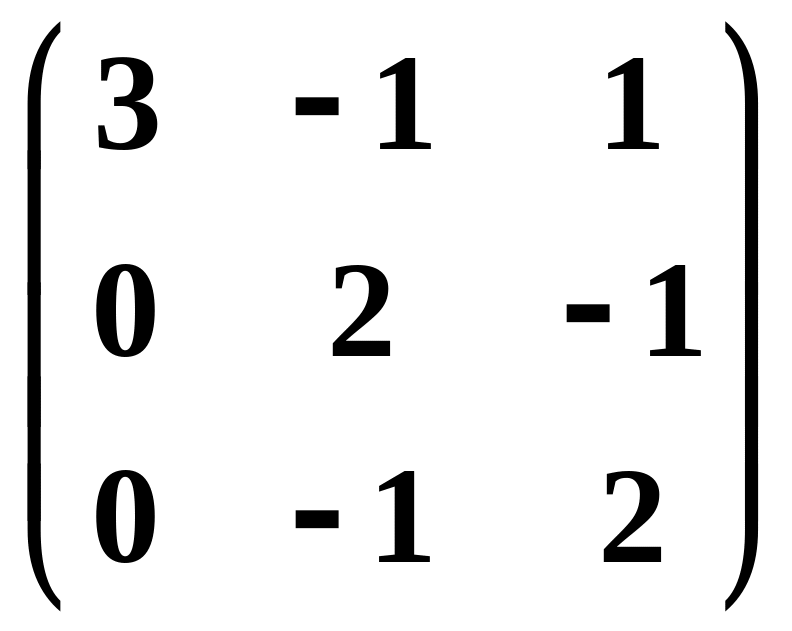Тема «Линейные пространства и их преобразования»
Вариант 4.
Найти координаты вектора в базисе , , , если он задан в базисе , , :
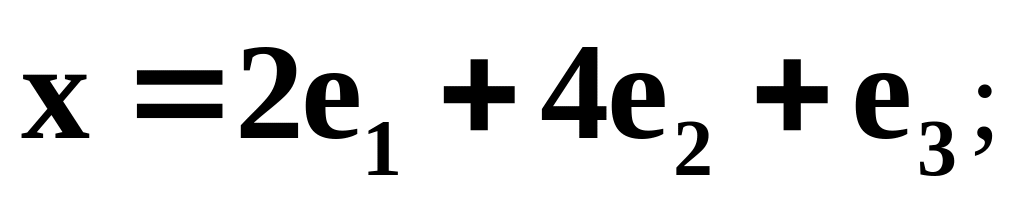
Найти фундаментальную систему решений и общее решение однородной системы линейных уравнений
Являются ли линейными преобразования отображения :
Пусть , – линейные преобразования пространства в себя:
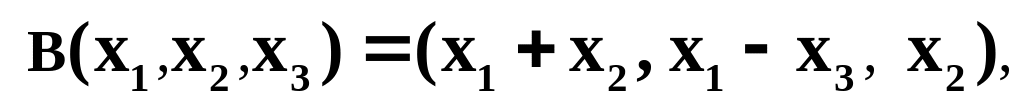где
– произвольный элемент
.
Найти
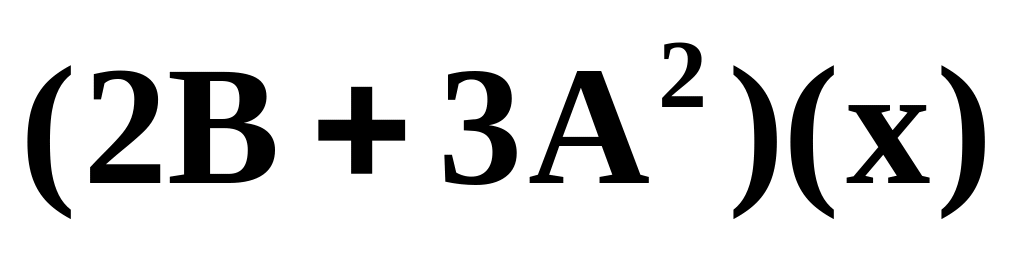.Линейное преобразование в базисе , , задано матрицей
.
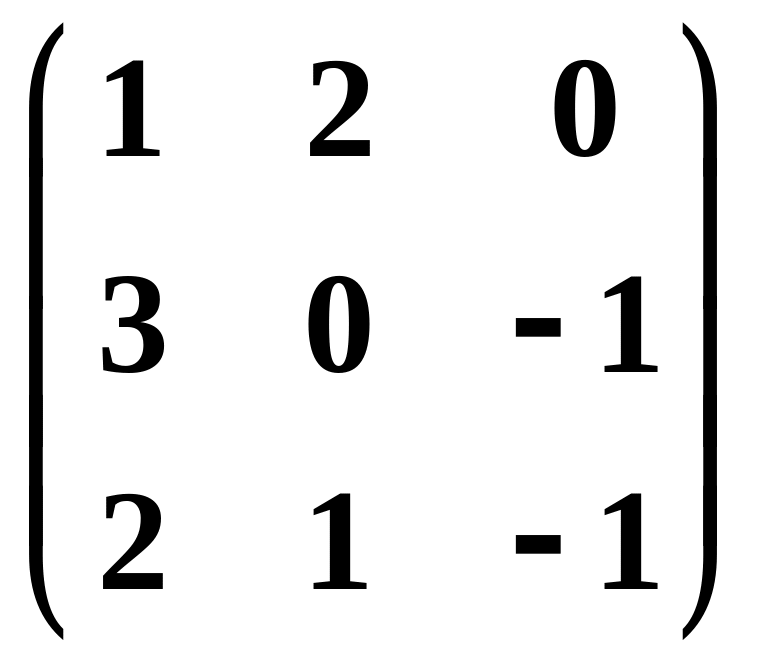Найти его матрицу в базисе
Найти собственные значения и собственные вектора линейного преобразования, заданного в некотором базисе матрицей
.
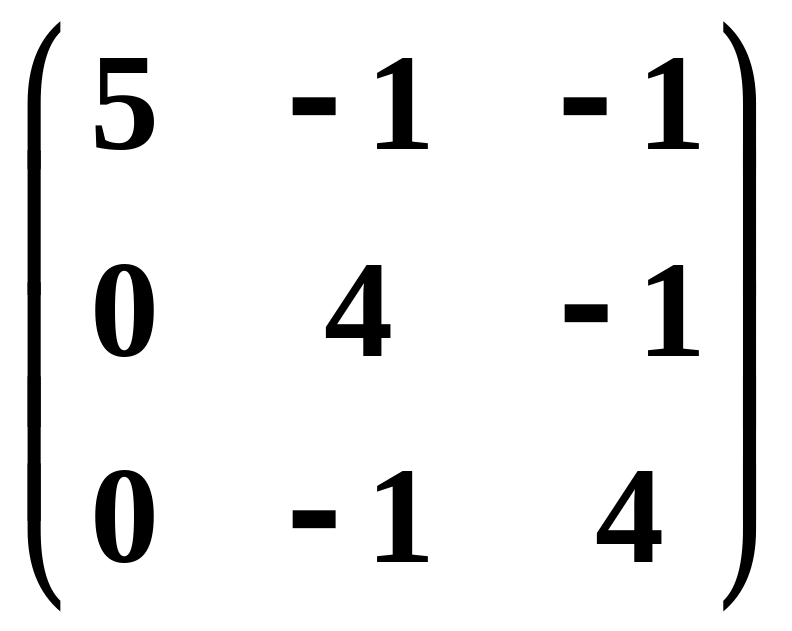Тема «Линейные пространства и их преобразования»
Вариант 5.
Найти координаты вектора в базисе , , , если он задан в базисе , , :
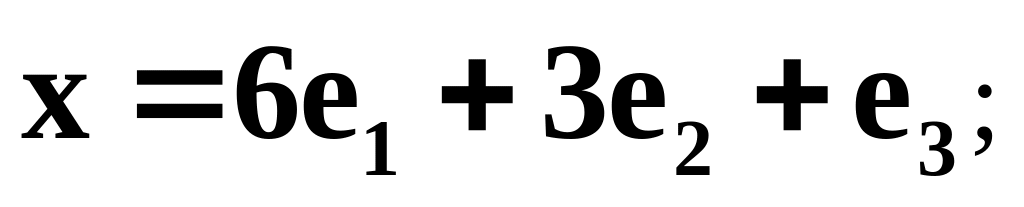
Найти фундаментальную систему решений и общее решение однородной системы линейных уравнений
Являются ли линейными преобразования отображения :
Пусть , – линейные преобразования пространства в себя:
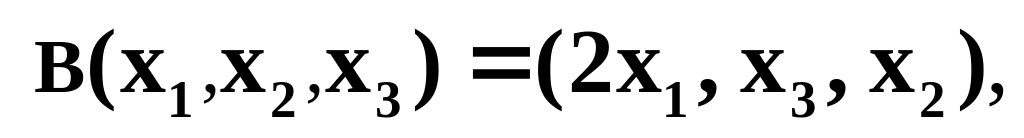где
– произвольный элемент
.
Найти
.Линейное преобразование в базисе , , задано матрицей
.
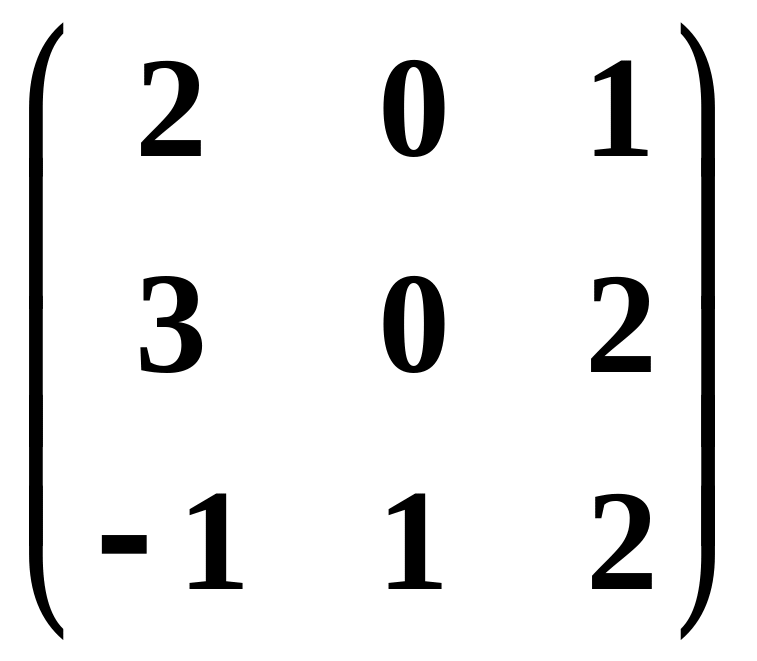Найти его матрицу в базисе
Найти собственные значения и собственные вектора линейного преобразования, заданного в некотором базисе матрицей
.