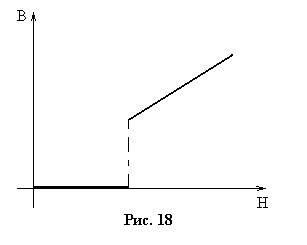
Р ешение: Экспериментально удалось получить зависимость критического поля от температуры – кривую, отделяющую нормальную область от сверхпроводящей:
В
сверхпроводящей фазе всегда
.
Это значит, что сверхпроводник является
диамагнетиком с
.
В свободной энергии необходимо учесть зависимость как от температуры так и от величины намагниченности
Такой термодинамический потенциал
минимален при заданных
и
.
Однако экспериментально контролировать
изменение
трудно, гораздо легче это делать для
внешнего поля
.
Введем термодинамический потенциал,
который минимален при заданных
и
.
.
Тогда
При изменении магнитного поля на величину
источники поля совершают работу над
единицей объема
.
Следовательно, при изменении поля то
до
источник поля совершает работу
.
Эта работа будет запасена в свободной энергии сверхпроводника
.
В точке перехода
,
а
– плотности свободной энергии нормального
металла.
(1)
и, следовательно
(2)
(то же для
)(при
фазовом переходе непрерывны как
так и
).
Последняя формула показывает, что при
данной температуре и
и энергетически выгодно нормальное
состояние, а при
– сверхпроводящее (
).
При
и нормальное состояние будет при любом
поле. Поскольку
,
то
Следовательно, сверхпроводящее состояние
более упорядочено (
).
При
и
.
Это значит, что при переходе при
не выделяется теплоты (фазовый переход
2-го рода). При
и при таком переходе выделяется теплота
(фазовый переход 1-го рода). Найдем эту
теплоту. При переходе из сверхпроводящей
фазы в нормальную
(
)–
теплота поглощается и наоборот - при
обратном переходе теплота выделяется.
В силу непрерывности
вдоль границы сверхпроводник - нормальный
металл в состоянии равновесия
.
Отсюда получаем вышеуказанную кривую фазового равновесия:
Но
,
а
,
поэтому теплота, выделяющаяся при
переходе:
(равно нулю если
).
Наконец, теплоемкость изменяется скачком при любой температуре:
.