Аксиомы вероятности.

Рассмотрим некоторую систему F подмножеств, множества элементарных событий «омега»={w_1, w_2,…,w_n}, элементы которой  ε= ε(w): = случайными событиями.

Множество F, содержащие: 1. множество «омега», - пустое множество; 2. наряду с каждой парой, принадлежащих ему элементов A,B, являющихся подмножествами «омега», также их пересечение, соединение и разность. ( , , A-B) (15)

I= алгеброй множеств (событий).

Аксиома определения вероятности:

1. F – является алгеброй множеств

2. Каждому множеству A F сопоставляется действительно число O(A) ≥0 называемое вероятностью события A.

3. P(«омега») = 1

4. Для всех A,B F, причем 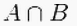= P(A+B)=P(A)+P(B) (16)

Система аксиом Колмогорова непротиворечива и не полна. Неполнота проявляется в том, даже для одного и того же множества элементарных событий «омега» вероятности можно выбрать разными способами. Однако, неполнота системы аксиом объективно обусловлена: в различных задачах встречаются явления , при изучении которых требуется рассматривать одинаковые множества случайных событий, но с различными вероятностями.

Система {«омега», F, D}!= полем вероятности, если F – алгебра множеств.

Аксиома непрерывности, расширенная теорема сложения и теорема о ?покрытиях?

Развитие теории для вероятностей числа событий, истребовала «расширения» как конечного множества элементарных событий «омега» до «омега»={w_1, w_2,…, w_n}, так и алгебра событий F до Борелевской алгебры, а также введение аксиомы непрерывности.

Алгебра F подмножеств множества «омега»: = Борелевской алгеброй. Если все счетные A_k множеств A_k F также принадлежат F.

Замечание: Борелевская алгебра часто: = «сигма»-алгебрами.

Аксиома 5 (непрерывности). Для убываний последовательности из F (A_1 A_2 A_3 …) (17), такой что A_k = (18), имеем P(A_k)=0 (19)

На основе аксиомы непрерывности Колмогоровым доказаны важные теоремы:

1. Расширенная теорема сложения: Если A, A_1, A_2… F и (22) A= A_k (20), то вероятность P(A) P(A_k) (21)

2. Теорема о покрытиях: Если A, A_1, A_2… F и (22) A 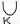A_k, то P(A)= P(A_k) (23)

При определении понятия вероятности следует указывать не только множества элементарных событий «омега», но и множества случайных событий F и определенную на нем функцию P.

Поле вероятностей {«омега», F, P}: = Борелевским комплексом вероятностей, если алгебра F – Борелевская алгебра.

Условная вероятность

Определение условной вероятности и вероятностного пространства. Теорема умножения вероятностей.

В основе определения вероятности события лежит некоторый комплекс условий «сигма»; если при вычислении вероятности события A никакие ограничения кроме комплекса условий «сигма» не налагаются, то такие вероятности: = безусловными. Однако, часто нужно найти вероятности событий при условии, что произошло некоторое вероятностное событие B.

Для любых событий A и B условной вероятностью события A при условии осуществления события B: = величина P(A/B)=P(AB)/P(B) (1)

Замечание: если все элементарные события имеют равные вероятности, то вероятность P(A/B) равна отношению числа N_AB – элементарных событий общих для событий A и B к числу N_B элементарных событий в событии B, то есть P(A/B)=P(A/B)=N_AB/N_B.

Иной вид формулы (1) P(AB)=P(A/B)P(B) (2) обычно: = как теорема умножения вероятностей.

Замечание: основные свойства вероятностей остаются справедливыми и для условных вероятностей.

Формула полной вероятности.

Пусть B_1, B_2,…,B_n полная группа событий, тогда любое событие A может одновременно осуществляться с некоторым B_i или A=AB_1 AB_2 … AB_N (4), так как события AB_i попарно несовместны, то их вероятности складываются.

Применяя к событию A при B=B_i (2?4?), получаем формулу полной вероятности:

P(A)- P(A/B_i)P(B_i) (5) Формула (5) удобна тем, что иногда проще оценить P(A/), чем прямо оценивать P(A).

Формула Байеса для вероятностей гипотез.

Пусть имеется группа взаимоисключающих и исчерпывающих всё пространство событий B_1, B_2,…, то есть таких, что каждое элементарное событие принадлежит одному из событий B_j и нужно оценивать вероятность наступлений события B_j при условии осуществления события A, так как необходимо вероятность P(B_j/A) можно представить в виде:

P(B_j/A)=P(AB_j)/P(A) (6), то подставляя в (6) формулы (2) и (3) получаем:

P(B_j/A)=P(B_j)P(A/B_j) / P(B_j0P(a/B_j) (7)

Если трактовать событие B_j как гипотезу, то есть научно обоснованные предположения, то (7) предоставляет известную формулу Байеса (1763г) для вероятностных гипотез.

Вероятности независимых событий.

Под испытанием будем понимать реализацию комплекса условий «сигма», в результате которого может произойти то или иное элементарное событие пространства «омега».

Испытание Бернулли.

Повторные независимые испытания, каждое из которых имеет два возможных исхода, а вероятности исходов постоянны: = испытаниями Бернулли.

Обычно вероятности двух исходов испытаний Бернулли обозначаются p или q, причем исход с вероятностью P: = «успехом», а с вероятностью Q: = «неудачей». P – У: q –Н.

Ясно, что вероятности p и q должны быть неотрицательны, а их сумма p+q=1 (1)

Таким образом, пространство элементарных событий каждого отдельного испытания Бернулли состоит их двух точек Удачи и Неудачи. Пространство элементарных событий для n испытаний Бернулли содержит уже 2^n точек или из n символов У и Н. каждая точка такого пространства представляет собой одни возможный исход составного испытания. Поскольку испытания независимы, то вероятности последовательных испытаний перемножаются. Другими словами вероятность n испытаний Бернулли – есть произведение полученных при замене результатов испытаний, предоставленных символами У и Н на p и q.

#: P{У, Н, У, У, Н,…}=pqppq…

Наиболее известным примером испытания Бернулли является последовательное бросание симметричной монеты, для которой p=q=1/2, однако, если монета, для несимметрична, то также считаем последовательные испытания независимыми, получаем испытания Бернулли, в котором вероятность успеха может быть произвольной.