
1.3. Пересечение и объединение множеств.
Пересечением множеств А и В называется множество, содержащее те и только те элементы, которые принадлежат множеству А и множеству В.(рис. 4)
![]()
В
А
рис. 4
Пересечение множеств А и В обозначают АВ. Таким образом, по определению пересечения можно записать:
А В == { х | х А и хВ}.
Рассмотрим свойства операции пересечения множеств.
1) А = ;
2) А А = А;
3) А В = В А (коммутативность);
4) А (В С) = (А В) С = А В С (ассоциативность);
5) А В А В = А;
6) А U = А
Объединением множеств А и В называется множество, содержащее те и только те элементы, которые принадлежат множеству А или множеству В. (рис. 5)
В
А
рис. 5
Объединение множеств А и В обозначают АВ. Таким образом, по определению объединения можно записать:
АВ = {х | х А или хВ}.
Рассмотрим свойства операции объединения множеств.
1) А = А;
2) А А = А;
3) А В = В А (коммутативность);
4) А (В С) = (А В) С = А В С (ассоциативность);
5) А В А В = В;
6) А U = U.
Если над множествами производятся операции пересечения и объединения и в записи выражения отсутствуют скобки, то сначала выполняют операцию пересечения, а затем операцию объединения.
Кроме перечисленных выше свойств операции пересечения и объединения, есть свойства, связывающие эти две операции.
Пересечение дистрибутивно относительно объединения, т. е. для любых множеств А, В и С имеем:
А (в с) = (А в) (А с).
Объединение дистрибутивно относительно пересечения, т. е. для любых множеств А, В и С имеем;
А (в с) = (А в) (А с).
Пример. Докажите, что А В А В = А
Решение. В данном примере необходимо доказать два утверждения:
1. если А содержится в В, то А В = А;
2. если А В = А, то А В.
Первое утверждение следует непосредственно из определения.
Докажем второе утверждение. Предположим, что АВ = А Докажем, что А В. Возьмем любой элемент а А и проверим, что а В. Тем самым докажем включение АВ ввиду определения этого отношения.
Итак, пусть а А. Тогда, в силу равенства А В = А получаем, что аА В, а это означает, по определению пересечения, что а В. Утверждение доказано.
1.4 Разность множеств. Дополнение подмножества.
Разностью множеств А и В называется множество, содержащее те и только те элементы, которые принадлежат множеству А и не принадлежат множеству В. (рис. 6)
В
А
рис. 6
Разность множеств А и В обозначают А\В. Таким образом, по определению разности А\В ={х | х А и хВ}.
В том случае, когда В А, разность множеств А и В называют дополнением подмножества В до множества А и обозначают ВА. Если В - подмножество универсального множества, то дополнение подмножества В до универсального множества обозначают В.
Справедливы следующие свойства разности и дополнения.
1) ` U;
2) U`= ;
3) А \ = А;
4) (А`)` = А;
5) А` А = ;
6) А` А = U;
7) А \ (В С) = (А \ В) \ С;
8) А\ (В\С) = (А\В) С, если С А ;
9) (А В) = А В;
10) (А в) = А В;
11) (А\ В) В = А, если В А;
12) А В=(А\ (А В)) В.
Пример. Даны множества А = { m, k, l, n } и В = { m, n, р, t, у }. Найдите множества А В, А В, А\В.
Решение. Множество А В состоит из тех и только тех элементов, которые принадлежат А и В, т.е. из элементов m и n: А В = {m, n}.
В множество А В входят элементы, принадлежащие А или в, т.е. А В = { m, k, l, n, р, t, у }.
Множеству А\В принадлежат те элементы множества А, которых нет в множестве В, т.е. А\В = { l, k }.
Упражнение 3.
1. Р - множество натуральных делителей числа 18. Q - множество натуральных делителей числа 24. Укажите характеристическое свойство элементов пересечения множеств Р и Q и перечислите его элементы.
2. Постройте диаграммы Эйлера для множеств А, В и С и укажите характеристическое свойство элементов множества А В С, если:
а) А - множество правильных треугольников,
В - множество треугольников,
С - множество четырехугольников,
б) А - множество параллелограммов,
В - множество прямоугольников,
С - множество четырехугольников,
в) А - множество прямоугольных треугольников,
В - множество равнобедренных треугольников,
С - множество равносторонних треугольников.
3. А - множество трапеций, В - множество четырехугольников, имеющих прямой угол, С - множество квадратов. Постройте диаграммы Эйлера для данных множеств и отметьте штриховкой области, изображающие множества:
а) А\В С б) (А\В) С в) (А С)\В
4. Известно, что А, В и С - подмножества универсального множества U и АВ С Постройте диаграммы Эйлера для данных множеств и отметьте штриховкой области, изображающие множества:
а) А\В С`, б) (А В)` С, в) (А` В`)\С, г) А` В\С,
д) А В\С, е) (А\В)` С, ж) А`\В`\С, з) (А В)`\С.
5. Докажите, что А\В = А\А В.
6. Докажите, что А\(В С) = (А\В) (А\С).
7. Укажите характеристическое свойство множеств:
а\в с, а` В` с, (А\ В)` \ С, а` в \ с`, а\в` с,
если А = { х | хR, -1 < х < 3}
В
= { х
| хR,
х
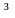 2}
2}
С = { х | хR, 0 < х < 5}
8. Выясните па основании каких законов операций над множествами произведены следующие преобразования:
а) (А В) С = А (В С) = А (С В)
б) (А в) с = А с в с = с А с в
в) А В А` С = А А` В С = (А А`) (В С) =
г) (А В)А = (А` В) А = (А` А) В =
