2.3. Графический метод определения констант дифференциального кинетического уравнения

Определим константы дифференциального кинетического уравнения для следующей реакции:

аА + bB → продукты.

Зависимость скорости от концентраций выражается уравнением (2.3)

.

Прологарифмируем это выражение

.

(2.4)

Так как величины k, n и m для рассматриваемой реакции (при T = const) являются постоянными и не зависят от концентрации реагентов, то для их нахождения достаточно определить зависимость скорости реакции от концентрации одного из реагентов при фиксированной концентрации другого реагента.

Пусть в трех опытах концентрация вещества А будет постоянной и равной [A]₀, тогда в уравнении (2.4) сумма ( ) будет тоже величиной постоянной, обозначим ее

.

Тогда уравнение (2.4) можно переписать как

.

(2.5)

Зависимость (2.5) представляет собой в координатах ln[B] — уравнение прямой линии, тангенс угла наклона которой к оси абсцисс численно равен порядку реакции по веществу В.

По экспериментальным данным строят график зависимости от ln[B] (рис. 3) и находят порядок реакции по веществу B

.

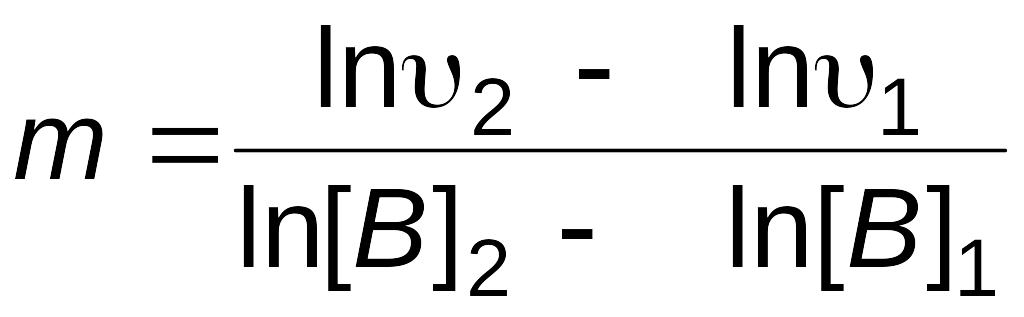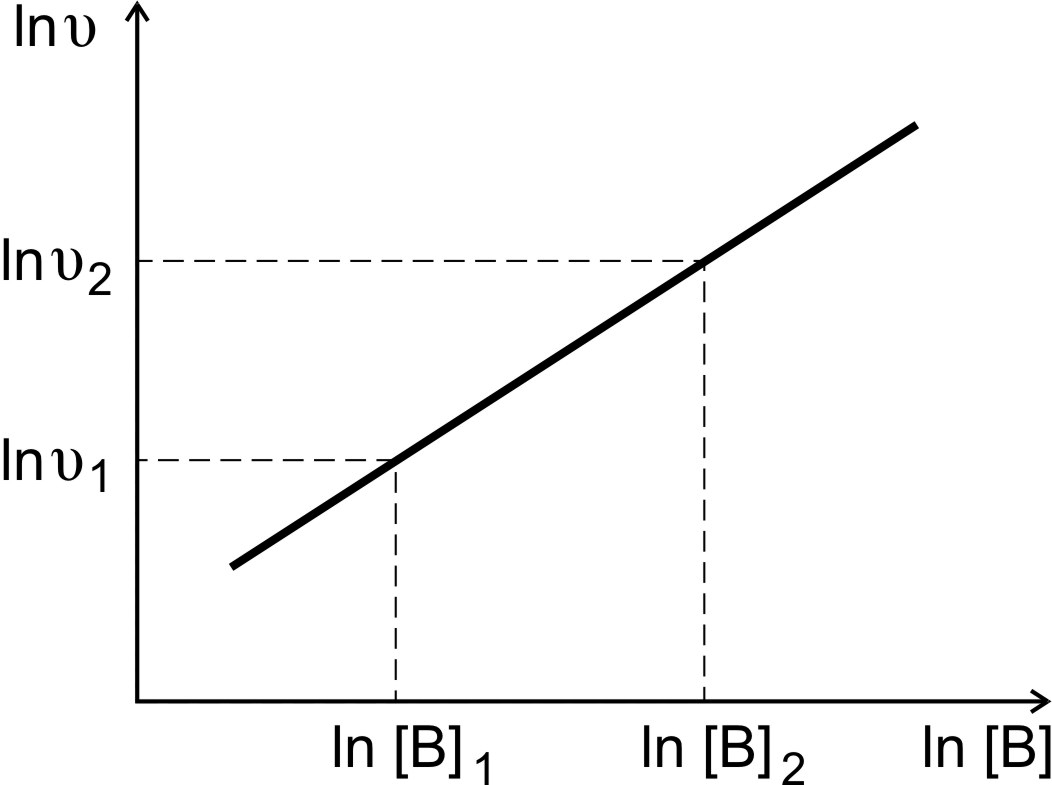
Рис.3. Определение порядка реакции по веществу В

В последующих опытах определяют скорость реакции при различных исходных концентрациях вещества А и постоянной концентрации [B]₀. Находят порядок реакции по веществу А

.

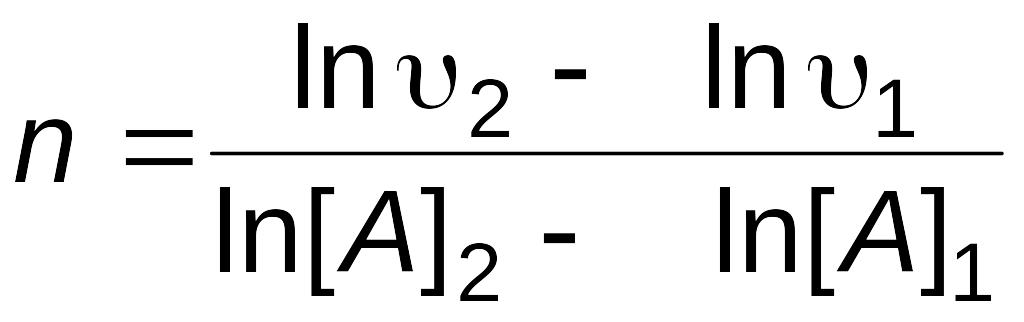Из уравнения (2.3) с учетом найденных порядков реакции по веществам А и В рассчитывают константу скорости

,

где , [A]_i, [B]_i - экспериментальные данные, относящиеся к одному опыту.

2.4. Зависимость концентрации реагирующих веществ от времени для реакции первого порядка. Интегральное кинетическое уравнение

На практике чаще всего интересует не само значение скорости химической реакции, а то, сколько вещества израсходовано или образовалось к определенному моменту времени после начала реакции.

Рассмотрим эту задачу на примере реакции первого порядка

А  продукты.

Скорость такой реакции выражается следующим уравнением:

.

(2.6)

В дифференциальном виде

.

(2.7)

Перепишем это уравнение в следующем виде:

,

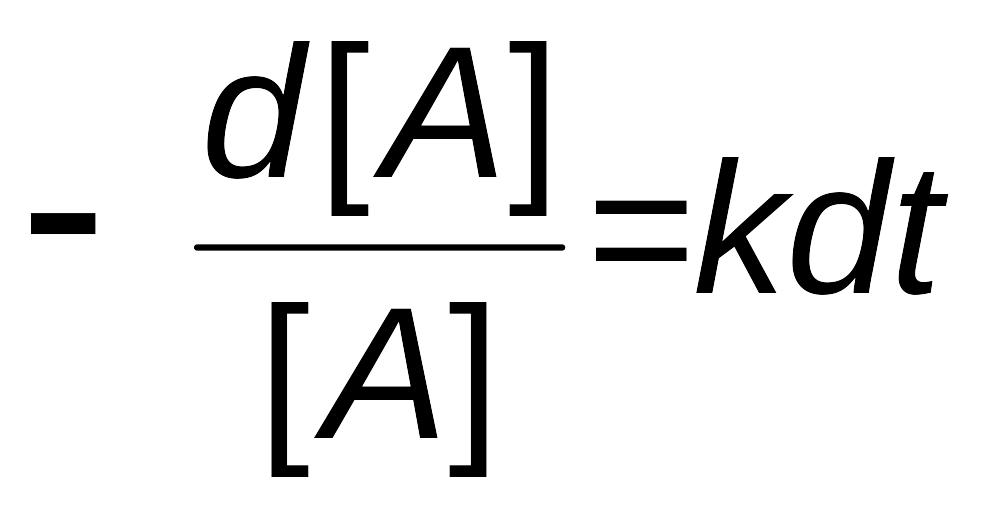и возьмем определенный интеграл от обеих частей уравнения от исходного состояния ([A]₀, t₀ = 0) до текущего момента ([A]_t, t):

.

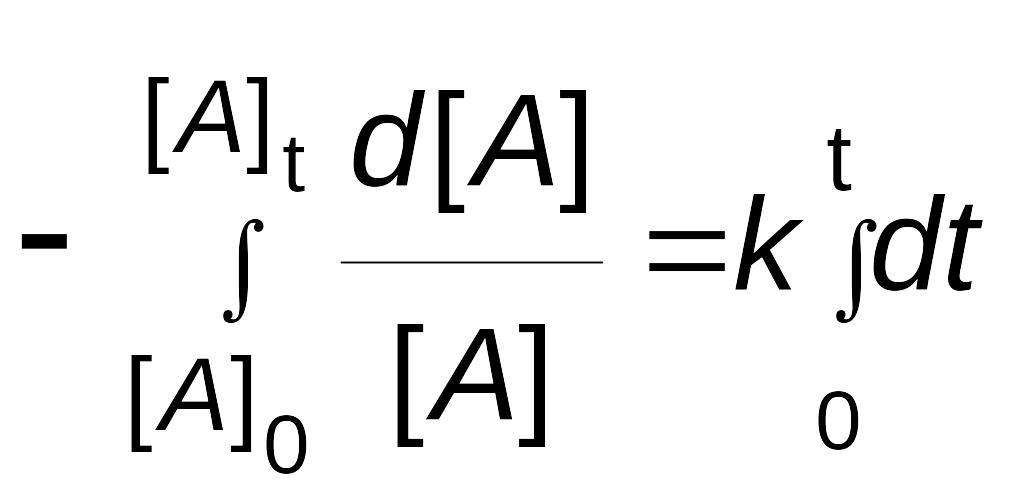Решение этого уравнения приводит к следующей зависимости:

(2.8)

или

.

(2.9)

Соотношения (2.8) и (2.9) являются интегральными кинетическими уравнениями реакции первого порядка.

Зная исходную концентрацию вещества [A]₀ и константу скорости реакции k, можно рассчитать концентрацию [A]_t через любое время t после начала реакции.

Если же известны исходная концентрация [A]₀ и концентрация реагирующего вещества [A]_t через какое-то время t после начала реакции, то можно рассчитать константу скорости этой реакции

.

(2.10)

Часто для характеристики скорости реакции пользуются временем полупревращения t_1/2 (для реакции первого порядка чаще говорят «период полураспада»). t_1/2 - это время, за которое прореагирует половина исходного вещества . Тогда, исходя из уравнения (2.10), получим следующие зависимости:

;	(2.11)
.	(2.12)
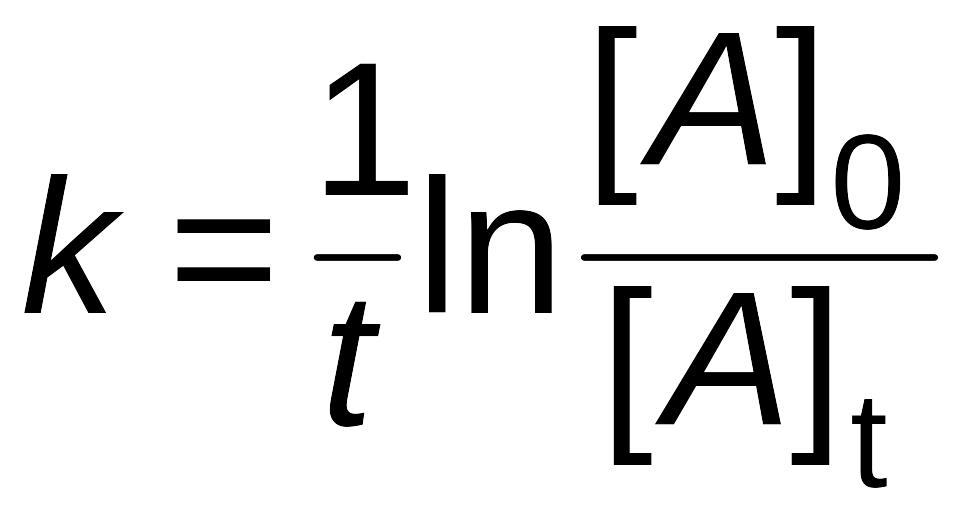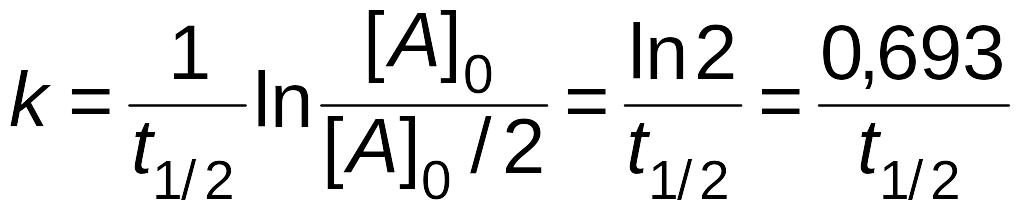