- •Содержание
- •Предисловие
- •1.Основные понятия компьютерной графики
- •2.История компьютерной графики
- •3.Аппаратное обеспечение компьютерной графики
- •3.1.Устройства вывода. Экраны
- •3.2.Устройства вывода твердых копий
- •3.3.Устройства ввода. Сканеры
- •3.4.Устройства ввода. Цифровые фотоаппараты
- •3.5.Устройства координатного ввода
- •4.Свойства растровых изображений
- •4.1.Форматы хранения растровых изображений
- •4.2.Цветовые модели растровых изображений
- •5.Аффинные преобразования на плоскости
- •5.1.Понятие однородных координат
- •5.2.Однородные координаты и преобразования в пространстве
- •6.Моделирование поверхностей
- •7.Основы твердотельного моделирования
- •7.1.Методы построения 3d тел
- •7.2.Анализ твердотельных моделей
- •8.Визуализация 3d моделей
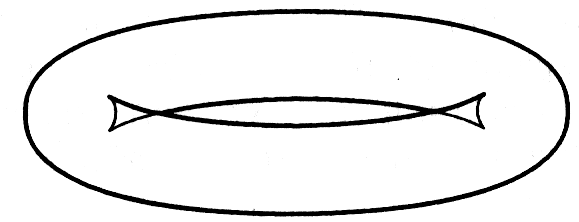
- •7Рис. 8.59 – Тор (а), параллельная (б) и центральная (в) проекции его линий очерка.
- •9.Программные технологии 3d графики
- •9.2.Интерфейс 3d api
- •9.3.Библиотека DirectX
- •9.4.Графический ускоритель
- •9.5.3D акселерация
- •10.Растровые алгоритмы
- •10.1.Удаление скрытых линий
- •11.Рендеринг
- •12.Компьютерная анимация
- •13.Предметный указатель
- •14.Список литературы
8.Визуализация 3d моделей
Созданную 3D модель поверхности или тела необходимо визуализировать – вывести на экран. При визуализации трехмерные объекты проецируются на плоскость, поэтому любая визуализация, в конечном счете, сводится к построению тех или иных проекций.
Все проекции делятся на два вида – центральные и параллельные (Рис. 8 .54).
|
|
|
|
а) |
б) |
Рис. 8.54 – Центральная (а) и параллельная (б) проекции.
У центральных проекций имеется точка наблюдения, в которой сходятся лучи, строящие проекцию. У параллельной проекции точка наблюдения вынесена в бесконечность. При центральной (перспективной) проекции изображение более близко к тому, которое образуется на сетчатке глаза, поэтому оно кажется более реалистичным. Однако центральные проекции искажают размеры объекта, поэтому их применение недопустимо в конструкторской документации.
Параллельные проекции любой точки объемного тела получаются очевидным образом путем построения перпендикуляра к проекционной плоскости, проходящего через заданную точку тела. Центральные проекции точек можно получить матричным методом при помощи перемножения соответствующих матриц преобразования.
Поскольку тела состоят в общем случае из плавных кривых, необходимо иметь способ построения проекций не просто отдельных точек, но и произвольных кривых линий. Для получения проекционного изображения кривой используется понятие полигона кривой – ломаной линии, состоящей из отрезков и аппроксимирующей заданную кривую (Рис. 8 .55).



Рис. 8.55 – Полигон кривой.
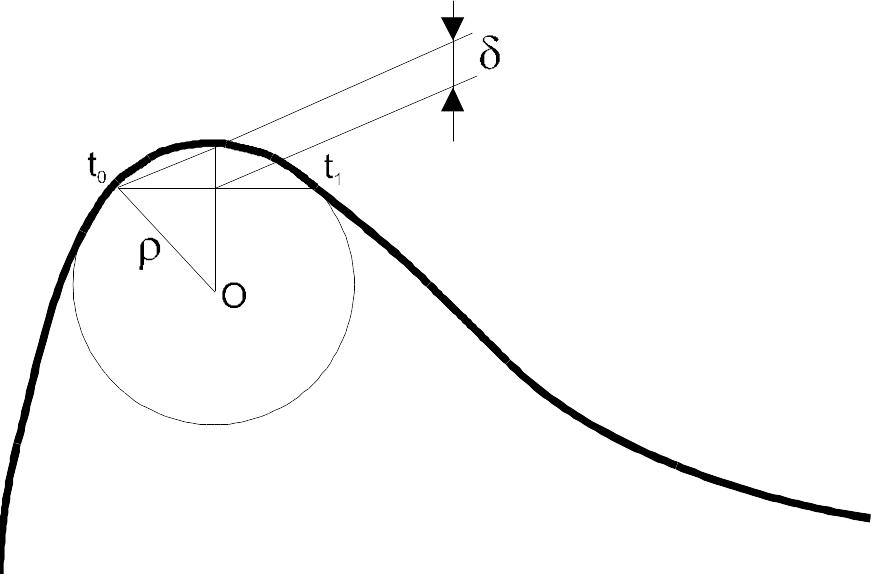
Рис. 8.56 – Определение шага полигона.
Точки на полигоне идут с некоторым шагом, который зависит от принятой точности отображения . Вычислим допустимый шаг точек полигона. Пусть кривая задана уравнением r(t). Точка t0 (Рис. 8 .56) лежит на кривой и является одной из вершин полигона. Нужно найти точку, являющуюся следующей вершиной полигона, причем отклонение полигона от кривой не должно превышать . Кривую в окрестностях точки t0 можно представить как сегмент окружности радиуса :
|
(0)
|
По теореме Пифагора длина хорды h, соединяющей точки t0 и t1, равна
|
(0)
|
Поскольку величина
h мала, можно считать,
что длина хорды примерно равна длине
дуги. Тогда приращение
![]() с учетом (0) равно
с учетом (0) равно
|
(0)
|
Если кривая резко
меняет направление, может потребоваться
заметное уменьшение величины
![]() для
соблюдения заданной точности отображения.
для
соблюдения заданной точности отображения.
Чтобы изобразить проекцию целого тела, а не отдельной кривой, используют наборы полигонов, называемые сетками. Обычно при визуализации строятся полигоны границ тела и нескольких его характерных линий (Рис. 8 .57).
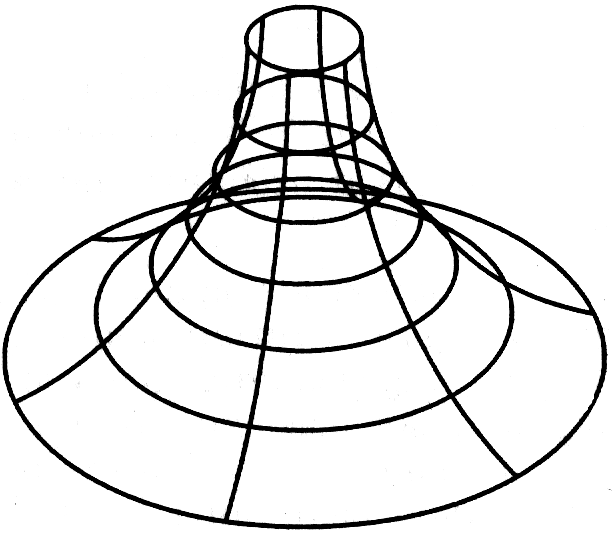

Рис. 8.57 – Сетка визуализации тела.
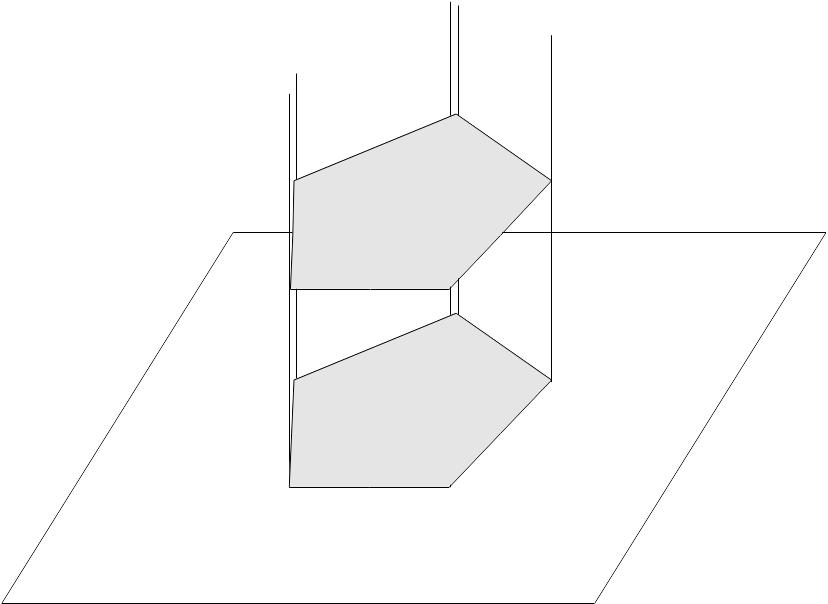
Для повышения информативности и качества визуализации в сетку полигонов добавляют так называемые линии очерка (Рис. 8 .58). Линия очерка отделяет видимую часть поверхности или грани от невидимой (при заданной точке зрения).

Рис. 8.58 – Линии очерка поверхности.
У одной поверхности может быть несколько линий очерка. Каждая линия очерка является либо замкнутой кривой, либо ее концы лежат на краях поверхности. При этом параллельные и центральные проекции линий очерка одного и того же тела могут заметно различаться (7Рис. 8 .59).
|
|
|
а) |
б) |
в) |