Содержание

ЛАБОРАТОРНАЯ РАБОТА № 1. 2

ЛАБОРАТОРНАЯ РАБОТА №3 5

ЛАБОРАТОРНАЯ РАБОТА №4 7

ЛАБОРАТОРНАЯ РАБОТА №5 9

ЛАБОРАТОРНАЯ РАБОТА № 1.

Тема: “Разработка математических моделей

и анализ динамики оптимизируемых систем”

Цель работы: Разработать математическую модель системы и проанализировать колебания оптимизируемой системы.

Задание:

1. Разработать программу и произвести численное интегрирование системы обыкновенных дифференциальных уравнений (1) на интервале времени 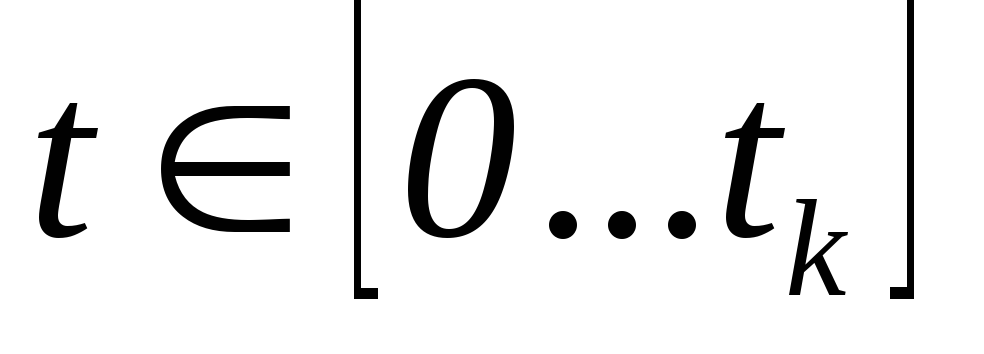при заданных начальных условиях и параметрах системы.

2. Исследовать свободные колебания системы, варьируя параметры 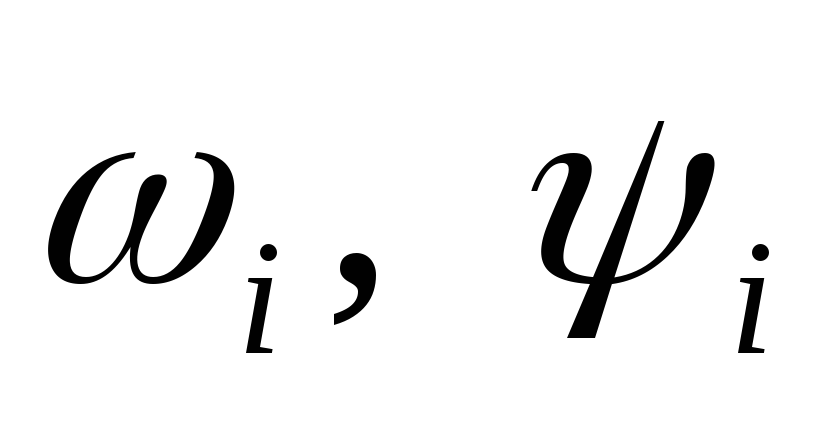(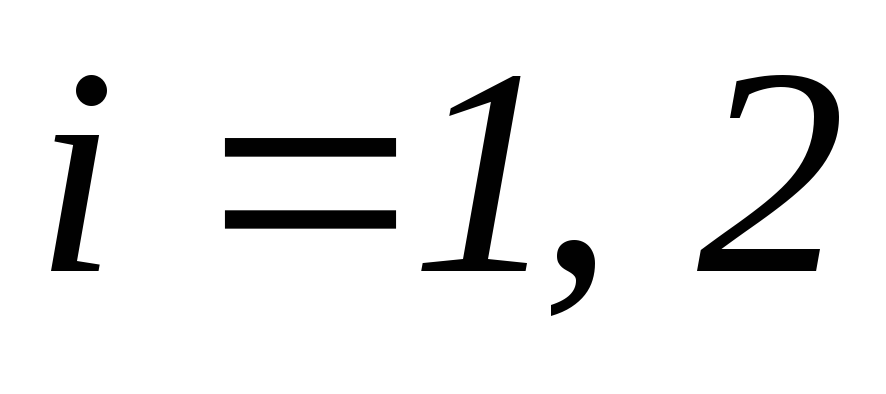) при заданных начальных условиях.

3. Исследовать вынужденные колебания системы, варьируя параметры (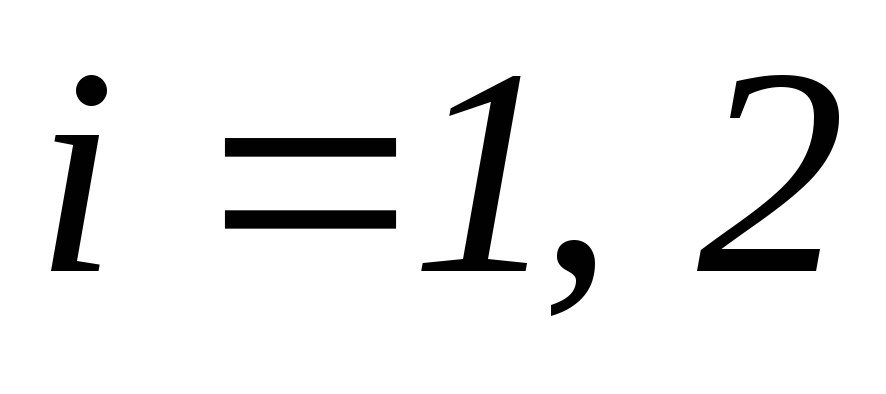) при различных частотах возмущающего воздействия .

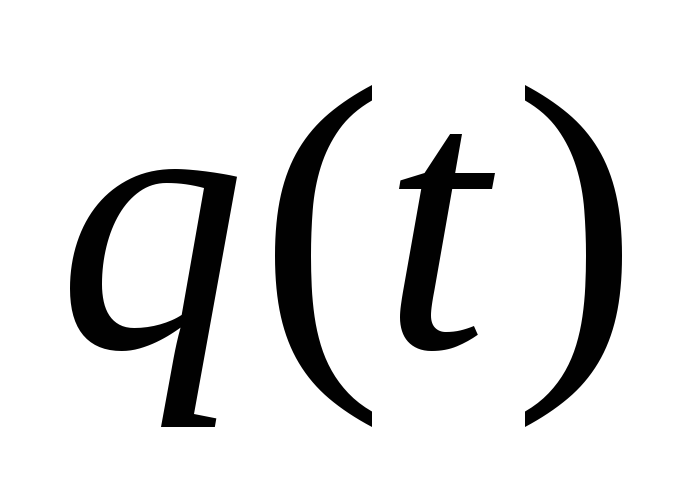Исходные данные

	5000	Kg
	100000	N/m
	50000	N*s/m
	500	Kg
	1000000	N/m
	20000	N*s/m

Исходные данные варьируются в соответствии с номером варианта (бригады) : .

Начальные значения переменных

	0.1	М
	0	М/s
	0	M
	0	M/s

Вычислить параметры, характеризующие колебания масс и , и вывести их на экран монитора в виде:

		1/s
		Безр.
		1/s
		Безр.

Параметры, характеризующие колебания масс и , рассчитываются по формулам:

; . . (3)

Параметры численного интегрирования

	0	S
	50	S
	0.005	S

Параметры гармонического возмущения

	0.1	M
	20	1/s

Вариант 1. Произвести вариацию параметра и оценить его влияние на частотные и диссипативные свойства динамической системы.

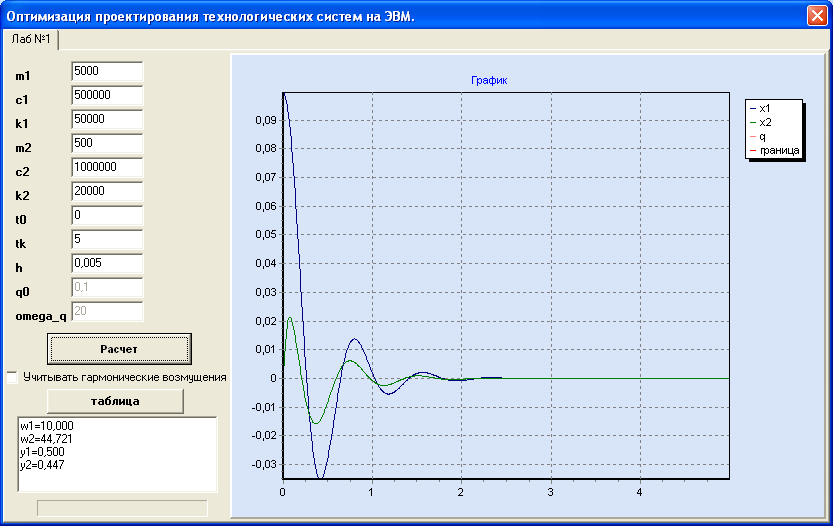
Выводы:

1. Параметр с₁ характеризует жесткость первой пружины.

2. Чем больше значение параметра с_1, тем медленнее система приходит в равновесное состояние.

ЛАБОРАТОРНАЯ РАБОТА № 2.

Тема: “ Моделирование внешней среды ”

Цель работы: Разработать программу для генерации случайного процесса и проанализировать корреляционную функцию и точность моделирования.

Задание:

1. Построить реализацию процесса заданной с корреляционной функцией на интервале времени с шагом и вывести ее график на экран монитора.

2. Вычислить для смоделированной реализации процесса 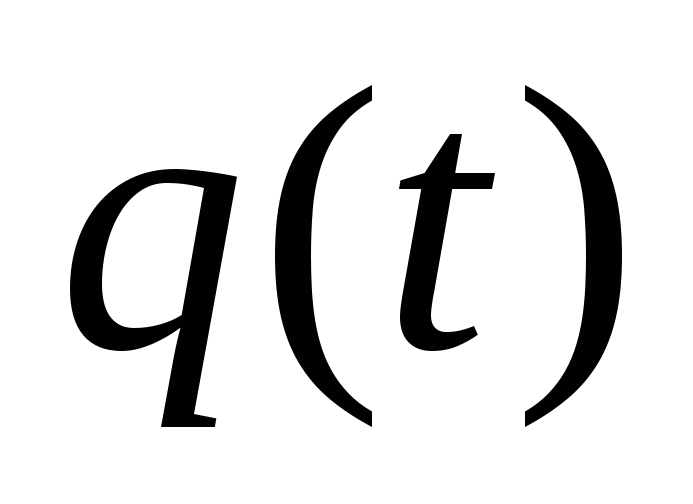оценку корреляционной функции и сравнить ее с исходной (заданной) корреляционной функцией 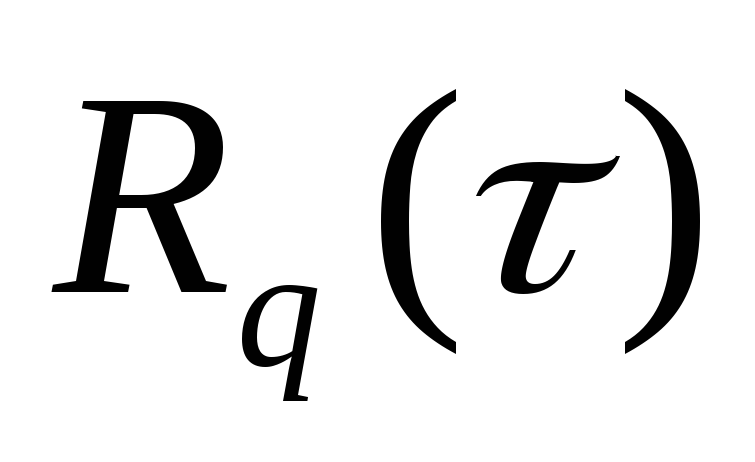. Оценить точность моделирования.

3. Произвести вариацию параметра и оценить его влияние на формируемый процесс.

Вариант 1. Произвести вариацию параметра и оценить его влияние на формируемый процесс.

Исходные данные

	0.05	m
	0.15	1/m
	0.20	1/m
	0.3	1/m
	10.0	m/s
	0.1	Безр.
	50.0	s
	0.001	s
	1.5	s
	0.01	s

Теоретические сведения:

При цифровом моделировании стохастических динамических систем возникает необходимость в формировании реализаций случайных возмущений по заданным статистическим характеристикам. На практике наиболее чаще всего встречаются нормальные случайные процессы. В этом случае корреляционная функция исчерпывающе описывает свойства случайного процесса.

Для формирования реализаций случайных процессов удобно использовать алгоритмы, основанные на линейном преобразовании последовательности [n] независимых чисел, распределенных по нормальному закону распределения, в последовательность q[n], коррелированную по определенному закону. Алгоритмы моделирования рассмотрены в работе [1, с.319-325].

Рассматривается нормально распределенный случайный процесс с корреляционной функцией:

,

где среднеквадратическое значение процесса;

,

где номер варианта;

;

; ; ;

, , и заданные константы.

Так, при алгоритм имеет вид:

q[n]=a₀[n]+b₁q[n-1],

где [n]-реализация независимых нормально распределенных чисел с параметрами m_=0, _=1.

Параметры алгоритма:

где h-заданный шаг дискретности аргумента; , , _E – коэффициенты; среднеквадратичное значение формируемого процесса .

Необходимо вывести на экран монитора рассчитанные на интервале времени значения оценок математического ожидания и среднеквадратичного значения процесса . Сравнить их с заданными значениями и оценить точность.

Результат работы

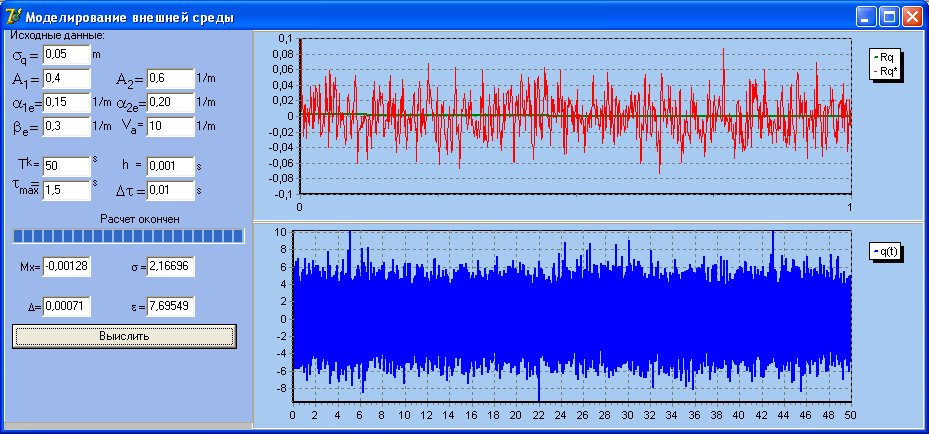
Выводы: параметр с₁ влияет на время кореляции, чем больше сила, тем больше время корелляции.

ЛАБОРАТОРНАЯ РАБОТА №3

Тема: «Статистический анализ систем методом Монте-Карло»

Цель работы: Разработать программу для статического анализа и получения зависимости критерия качества и ограничений.

Задание:

1. Произвести статистический анализ системы, используя разработанные ранее математическую модель системы (работа 1) и модель внешней среды (работа 2), варьируя указанный в задании параметр системы.

2. Построить зависимости критерия качества и ограничений от варьируемых параметров

Вариант 1. Произвести вариацию параметра .

Исходные данные

	-0.1	M
	0.1	M
		M
	0.999	Безр.
	0.999	Безр.

Формулы для вычисления оценки статистического критерия качества и ограничений второго рода

В качестве критерия принять среднеквадратичное значение ускорений массы в .

Ограничения вероятностей и невыбросов (невыходов) процесса , за уровни , а также процесса - за уровень являются ограничениями на функционалы от фазовых переменных системы (ограничения 2-го рода).

Ограничения 2-го рода задаются выражениями:

где заданные вероятности невыбросов;

;

;

заданные константы.

Вероятности невыбросов и вычисляются как математические ожидания соответствующих характеристических функций :

Результат работы

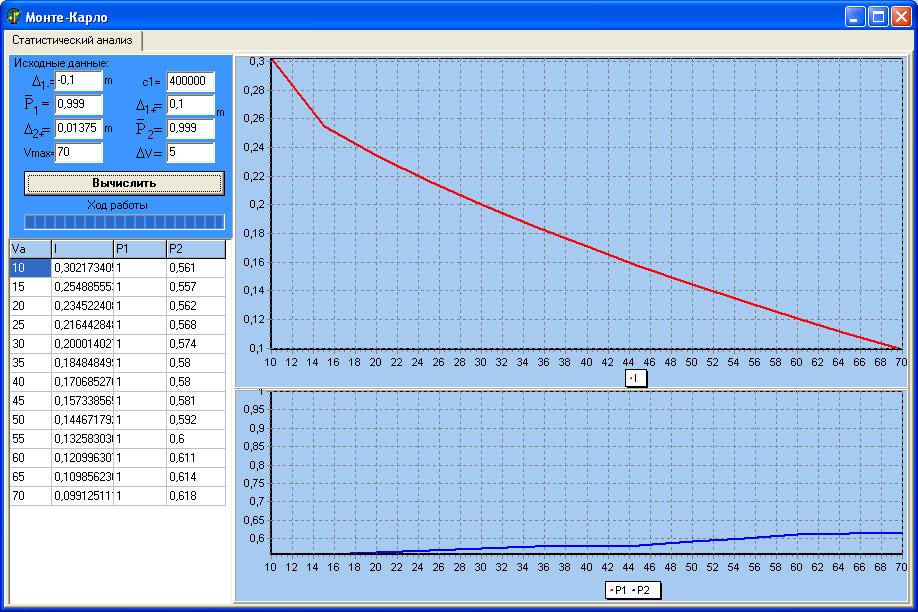
Выводы: параметр с₁ влияет на критерии качества.

ЛАБОРАТОРНАЯ РАБОТА №4

Тема: «Параметрическая оптимизация»

Цель работы: Разработать программу для статического анализа и получения зависимости критерия качества и ограничений.

Задание

1. Для заданного метода минимизации функций многих переменных разработать алгоритм и программу минимизации заданного критерия качества с учетом ограничений первого и второго рода.

1. Протестировать алгоритм и программу на функции Розенброка. Оценить эффективность (скорость сходимости) алгоритма и программы.

2. Используя математическую модель системы (работа 1), модель внешней среды (работа 2), алгоритмы вычисления критерия и ограничений (работа 3) произвести оптимизацию указанных параметров системы (коэффициенты c1, c2, k1, k2) таким образом, чтобы критерий качества принимал наименьшее значение при удовлетворении ограничений первого и второго рода. На экран монитора вывести таблицу рассчитанных величин, отражающих динамику поиска.

3. Оценить влияние на точность оптимизации параметра, определяющего конец поиска (условия прекращения поиска).

4. Осуществить спуск из различных начальных точек. Сравнить результаты и сделать заключение о том, имеет ли задача локальные минимумы.

Замечания

1. Процедуру минимизации оформить в виде отдельного UNIT без использования формы.

2. Недостающие исходные данные принять такими же, как и в предыдущих работах.

В качестве критерия качества системы принять среднее квадратическое значение ускорения выходной переменной (среднеквадратическое значение ускорения массы , выраженное в долях ).

Вариант 1. Произвести оптимизацию по одному параметру , а затем по четырем параметрам:

Результат работы

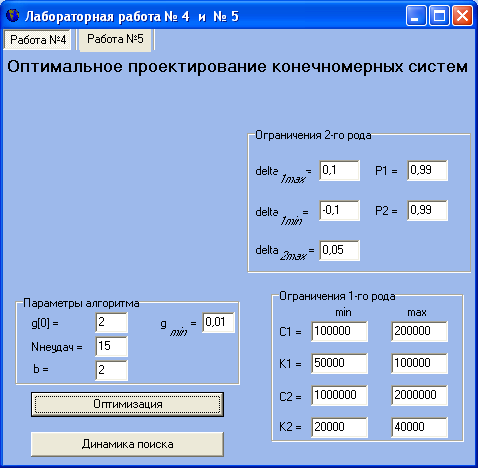
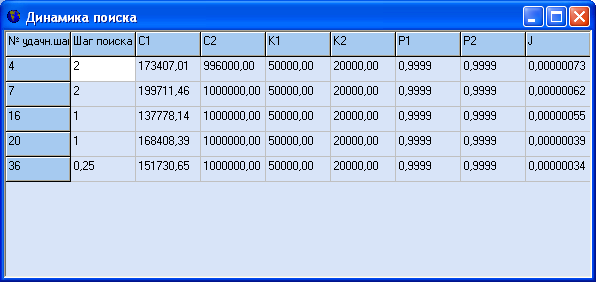
Выводы: провели параметрическую оптимизацию.

ЛАБОРАТОРНАЯ РАБОТА №5

Тема: «Оптимальное проектирование бесконечномерных систем

(систем управления)»

Задание

Уравнения движения системы, линейной относительно управляющей функции, заданы в виде:

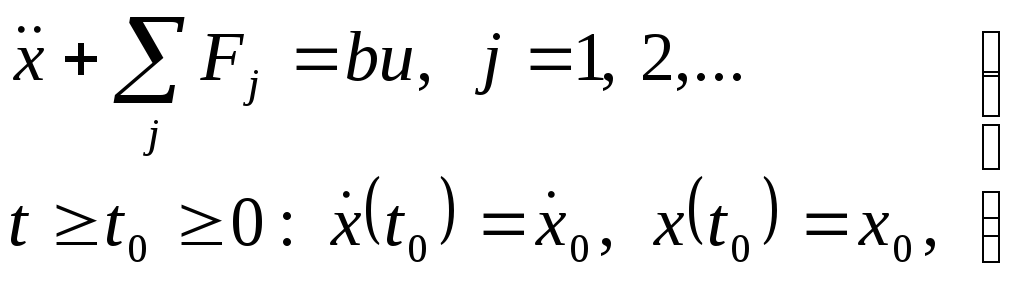
где заданные функции; константа:

Требуется найти управляющую функцию обеспечивающую для выходной переменной заданные желаемые свойства движения и кроме того, условия асимптотической устойчивости: при .

Вариант 1:

.

Результат работы

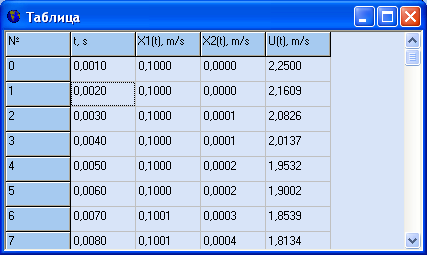
Вывод: провели оптимальное проектирование бесконечномерных систем.