6. Вязкая жидкость. Коэффициент вязкости

 вязкая жидкость- это подчиняющаяся в своём течении закону вязкого трения Ньютона, то есть касательное напряжение и градиент скорости линейно зависимы. Коэффициент пропорциональности между этими величинами известен как вязкость.

Простое уравнение, описывающее силы вязкости, возникающие в ньютоновской жидкости (которые во многом определяют ее поведение), основано на сдвиговом течении:

,

где

 — касательное напряжение, вызываемое жидкостью [Па]

 — динамический коэффициент вязкости — коэффициент пропорциональности [Па·с]

 — производная скорости в направлении, перпендикулярном направлению сдвига [с⁻¹].

7. Движение тела в вязкой жидкости. Формула Стокса для шарика и границы ее

применимости.

На тело, движущееся в жидкости или газе, действуют две силы (равнодействующую их обозначим R), одна из которых (R_x) направлена в сторону, противоположную движению тела (всторону потока), — лобовое сопротивление, а вторая (R_y) перпен­дикулярна этому направлению — подъемная сила 

Формула Стокса — Эйнштейна

Величина подвижности не всегда легко определяется, поэтому если предположить, что числа Рейнольдса малы, то для силы сопротивления, испытываемой макроскопическим шариком (частицей), можно использовать формулу Стокса

где   — вязкость жидкости,   — радиус частицы.

Таким образом, получается выражение:

8. Течение в трубах. Закон Пуазейля и границы его применимости. Гидравлическое сопротивление.

Уравнение или закон Пуазёйля (закон Хагена — Пуазёйля или закон Хагена — Пуазёйля) — закон, определяющий расход жидкости при установившемся течении вязкой несжимаемой жидкости в тонкой цилиндрической трубе круглого сечения.

где

•  — расход жидкости в трубопроводе;

•  — диаметр трубопровода;

Закон Пуазёйля работает только при ламинарном течении и при условии, что длина трубки превышает так называемую длину начального участка, необходимую для развитияламинарного течения в трубке.

 гидравлическое сопротивление — безвозвратные потери удельной энергии (переход её в теплоту) на участках гидравлических систем (системгидропривода, трубопроводах, другом гидрооборудовании), обусловленные наличием вязкого трения

Гидравлические потери принято разделять на два вида:

• потери на трение по длине — возникают при равномерном течении, в чистом виде — в прямых трубах постоянного сечения, они пропорциональны длине трубы;

• местные гидравлические потери — обусловлены т. н. местными гидравлическими сопротивлениями — изменениями формы и размера канала, деформирующими поток. 

9. Ламинарное и турбулентное течение. Число Рейнольдса.

Ламина́рное тече́ние — течение, при котором жидкость или газ перемещается слоями без перемешивания и пульсаций (то есть беспорядочных быстрых изменений скорости и давления).

Турбулентное течение течение жидкости или газа, характеризующееся беспорядочным, нерегулярным перемещением его объёмов и их интенсивным перемешиванием но в целом имеющее плавный, регулярный характер.

Число Рейно́льдса ( ), — безразмерная величина, характеризующая отношение нелинейного и диссипативного членов в уравнении Навье — Стокса^[1]. Число Рейнольдса также считается критерием подобия течения вязкой жидкости.

Число Рейнольдса определяется следующим соотношением:

где

•  — плотность среды, кг/м³;

•  — характерная скорость, м/с;

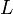•  — характерный размер, м;

•  — динамическая вязкость среды, Н·с/м²;

•  — кинематическая вязкость среды, м²/с( ) ;

•  — объёмная скорость потока;

•  — площадь сечения трубы.