- •Лабораторная работа № 14.
- •Описание конструкции и приборов.
- •Контрольные вопросы
- •Исходные положения
- •Лабораторная работа № 15.
- •Лабораторная работа № №16.
- •Постановка и выполнение опытов
- •Теоретическое определение величин «лишних» неизвестных
- •Сравнение результатов и выводы
- •Контрольные вопросы.
- •Лабораторная работа №17.
- •Лабораторная работа №18.
- •Постановка опыта
- •Порядок проведения опыта и обработка результатов.
- •Теоретическое определение величины и направления прогиба при косом изгибе.
- •Контрольные вопросы.
- •Лабораторная работа № 19.
- •Постановка опыта
- •Порядок проведения опыта и обработка результатов.
- •Теоретическое определение нормальных напряжений
- •Контрольные вопросы.
- •Лабораторная работа №20.
- •Постановка опыта
- •Порядок проведения опыта и обработка результатов.
- •Теоретическое определение напряжений и вертикального перемещения концов бруса.
- •Сравнение результатов и выводы.
- •Контрольные вопросы.
- •Лабораторная работа № 21.
- •Исходные положения
- •Теоретическое определение критической силы и критического напряжения.
- •Сравнение результатов и выводы
- •Контрольные вопросы.
- •Лабораторная работа №22.
- •Постановка испытания
- •Методика проведения опыта
- •Сравнение результатов опыта и выводы
- •Контрольные вопросы.
- •Лабораторная работа № 23
- •Постановка опыта.
- •Методика проведения опытов и их результаты
- •Теоретические расчеты
- •Сравнение результатов и выводы.
- •Контрольные вопросы:
- •Лабораторная работа № 24.
- •Контрольные вопросы.
Лабораторная работа №18.
КОСОЙ ИЗГИБ КОНСОЛЬНОЙ БАЛКИ
Цель работы: проверка правильности теоретических формул для определения величины и направления прогиба при косом изгибе.
Постановка опыта
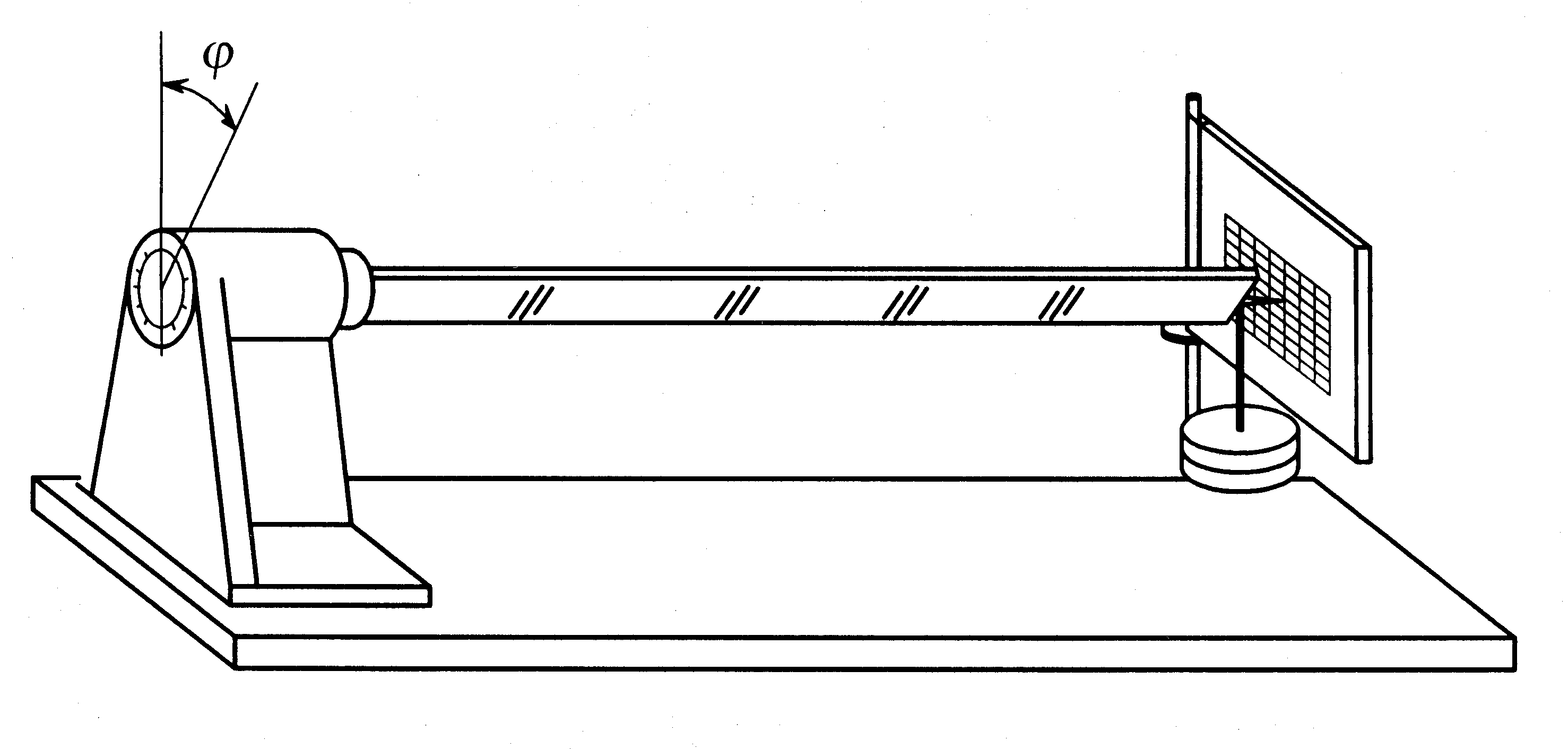
Изучить явление косого изгиба можно на модели консольной балки прямоугольного поперечного сечения. Схема установки показана на рис.18.1.
|
Рис. 18.1 |
Один
конец испытываемой балки, повернутой
в плоскости поперечного сечения под
заданным углом
![]() к вертикали, защемлен. Свободный конец
балки снабжен крюком для подвешивания
груза и острием, которое служит для
отметок прогибов. Отметки в виде точек
получаются путем прижатия экрана с
укрепленной на нем миллиметровкой к
острию штифта на каждой ступени
нагружения.
к вертикали, защемлен. Свободный конец
балки снабжен крюком для подвешивания
груза и острием, которое служит для
отметок прогибов. Отметки в виде точек
получаются путем прижатия экрана с
укрепленной на нем миллиметровкой к
острию штифта на каждой ступени
нагружения.
Порядок проведения опыта и обработка результатов.
Балка поворачивается в плоскости поперечного сечения на заданный угол , закрепляется в таком положении.
На экране крепится листок миллиметровки, его вертикальность выверяется по отвесу. Острым концом штифта делается начальная отметка при F=0.
Нагрузка увеличивается равными ступенями. На каждой последующей ступени загружения делается накол точки на миллиметровке.
С помощью опытных точек определяются основные результаты эксперимента:
а)
величина полного перемещения
![]() от одной ступени нагрузки
от одной ступени нагрузки
![]() ;
;
б)
угол
![]() наклона плоскости прогиба к вертикали
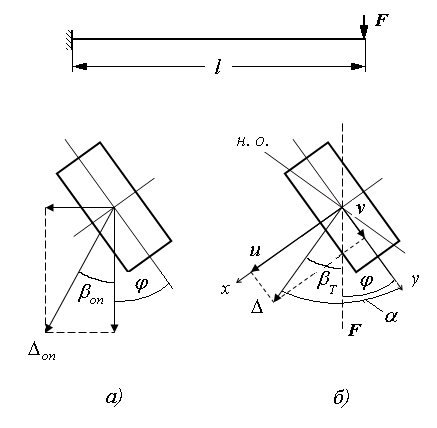
(рис.18.2,а).
наклона плоскости прогиба к вертикали
(рис.18.2,а).
Теоретическое определение величины и направления прогиба при косом изгибе.
Согласно принципу независимости действия сил величина полного перемещения (рис.18.2, б) свободного конца балки может быть вычислена как геометрическая сумма двух плоских прогибов по формуле
![]() ,
(18.1)
,
(18.1)
где
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
|
Рис. 18.2 |
Угол наклона линии прогиба к вертикали вычисляется так:
![]() ,
(18.2)
,
(18.2)
где
![]() ;
;
- заданный угол.
В выводах следует отметить, насколько подтверждаются опытом теоретические результаты, полученные по формулам (18.1) – (18.2).
Контрольные вопросы.
Какой изгиб называется косым?
В чем принципиальное различие между плоским и косым изгибом?
В чем заключается общий подход расчета стержней на сложное сопротивление?
Каковы результаты опыта: как ориентирована плоскость изгиба оси балки при косом изгибе?
Как теоретически определяется положение нейтральной линии при косом изгибе, а также величина и направление полного прогиба
 ?
?
Лабораторная работа № 19.
ВНЕЦЕНТРЕННОЕ РАСТЯЖЕНИЕ СТАЛЬНОЙ ПОЛОСЫ
Цель работы: экспериментальное определение нормальных напряжений в случае внецентренного растяжения стержня и сравнение опытных данных с теоретическими.
Постановка опыта
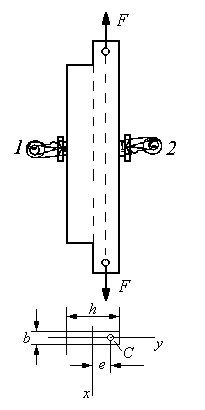
В опыте используется стальной образец прямоугольного поперечного сечения (рис.19.1).
Экспериментальное
определение нормальных напряжений
![]() сводится к измерению относительных
продольных линейных деформаций на
каждой ступени нагружения с последующим
применением закона Гука в форме
сводится к измерению относительных
продольных линейных деформаций на
каждой ступени нагружения с последующим
применением закона Гука в форме
![]() ,
где Е – модуль продольной упругости.
Линейные деформации измеряются на
боковых гранях, перпендикулярных
плоскости изгиба, где влияние
эксцентриситета наиболее сильно
сказывается.
,
где Е – модуль продольной упругости.
Линейные деформации измеряются на
боковых гранях, перпендикулярных
плоскости изгиба, где влияние
эксцентриситета наиболее сильно
сказывается.
|
Рис. 19.1 |
Для измерения линейных деформаций используются рычажные тензометры А1, А2.