Ранг матрицы

Если определитель – числовая характеристика, определяемая только для квадратной матрицы, то для произвольной матрицы можно ввести числовую характеристику, называемую рангом матрицы. Рассмотрим для некоторой матрицы A размера всевозможные квадратные матрицы, полученные из A вычеркиванием строк и столбцов. Пусть существует такая квадратная матрица, размера ( ), определитель которой отличен от нуля, в то время как все квадратные матрицы большего размера имеют нулевые определители. Тогда говорят, что матрица A имеет ранг, равный p ( ).

Для вычисления ранга матрицы с помощью пакета программ MAXIMA используют команду rank:

matr.wxm

Справедлива следующая теорема: система

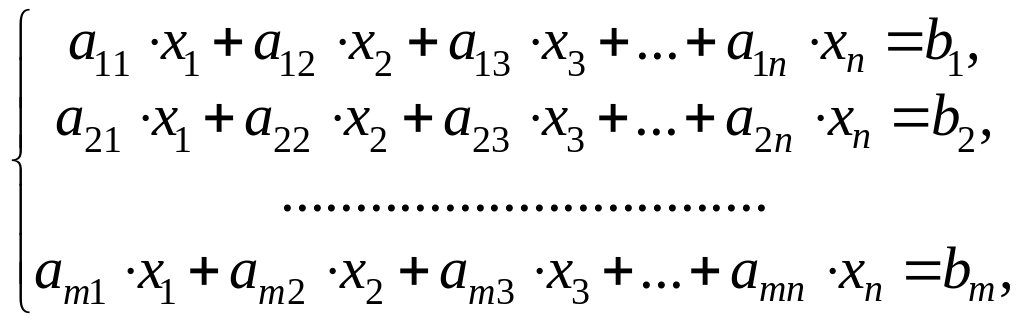
совместна (то есть имеет решения) тогда и только тогда, когда ранги главной матрицы системы

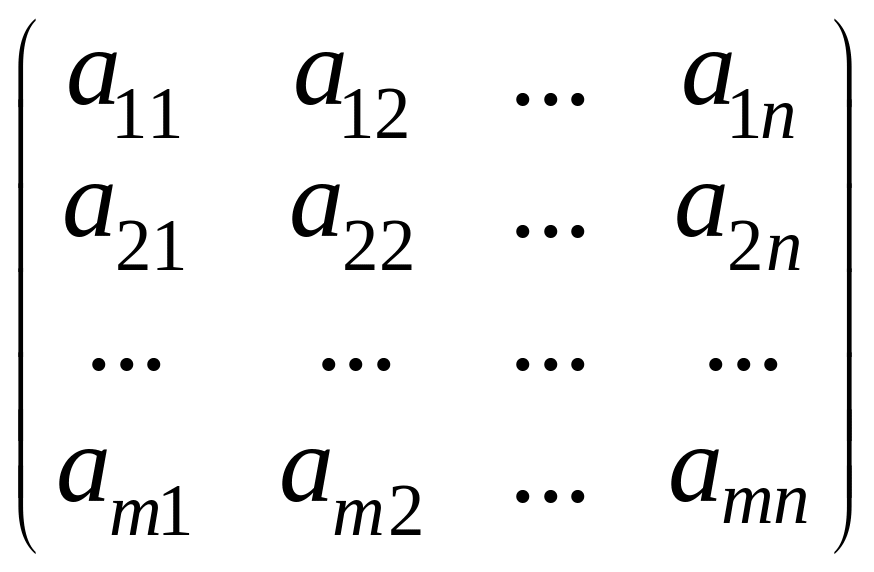
и расширенной матрицы системы

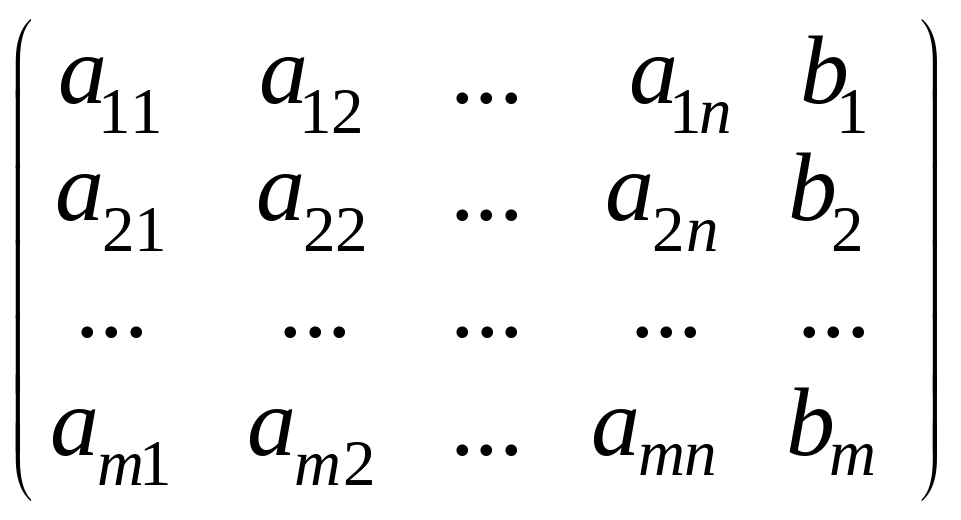
совпадают.

Прямые на плоскости и плоскости в пространстве

Продемонстрируем, как теория линейных систем иллюстрируется геометрическими примерами.

Рассмотрим множество точек плоскости XOY. Как известно, каждая точка на плоскости может быть задана с помощью двух декартовых координат и , которые являются координатами проекций точки на координатные оси.

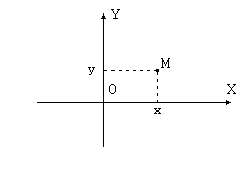
Простейшей плоской кривой является прямая – геометрическое место точек, соединив любые две из которых, мы получим отрезок, параллельный заданному вектору.

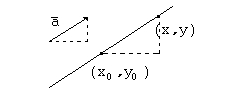
Рассмотрим прямую в плоскости XOY. Фиксировать прямую, параллельную данному вектору с координатами мы сможем, задав одну точку с координатами , через которую прямая проходит. Выберем на прямой произвольную точку с координатами . Тогда из подобия соответствующих треугольников имеем

. (1)

Вводя угловой коэффициент прямой (тангенс угла, образуемого прямой с положительным направлением ), мы получим из (1) уравнение прямой с угловым коэффициентом: .

Приравнивая нулю координаты направляющего вектора и , получим прямые, параллельные координатным осям: и .

Прямая на плоскости может задаваться не только точкой и направляющим вектором, но и двумя различными точками.

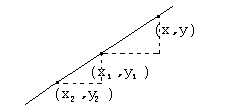
Составляя пропорции сторон подобных треугольников, получим соотношение . Это линейное соотношение представляет собой уравнение прямой, проходящей через две различные точки.

Любая прямая на плоскости xoy представляется линейным уравнением вида . И наоборот, любое линейное уравнение вида описывает прямую на плоскости xoy.

Взаимное расположение двух прямых на плоскости. Рассмотрим две прямые, задаваемы уравнениями и .

Возможны следующие случаи взаимного расположения этих прямых: 1) прямые совпадают, 2) прямые параллельны, 3) прямые пересекаются в одной точке. Исследуем соотношение между коэффициентами уравнений прямых в каждом из перечисленных случаев.

В случае 1) оба уравнения, описывающие одну и ту же прямую, должны совпадать или отличаться коэффициентом, на который можно сократить.

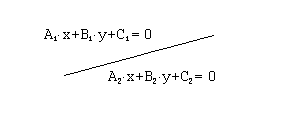
Таким образом, в данном случае .

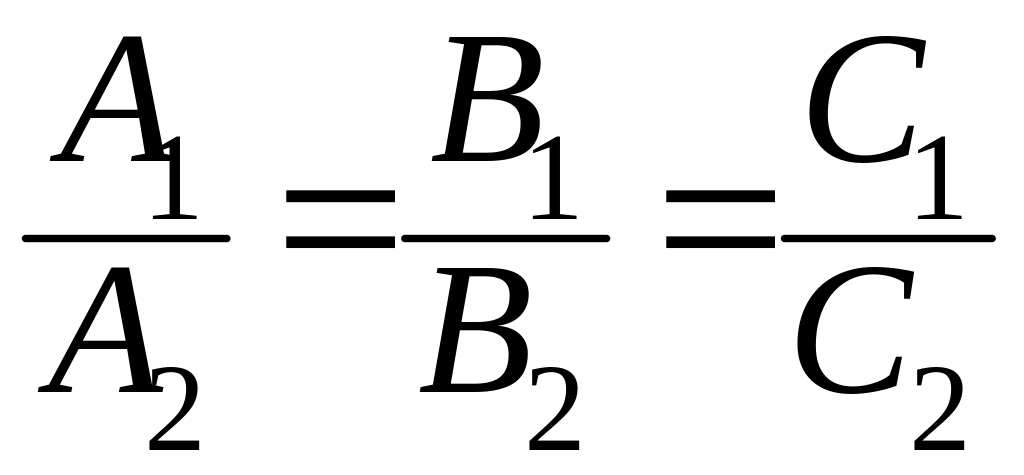В случае 2) угловые коэффициенты обеих прямых одинаковы. То есть,

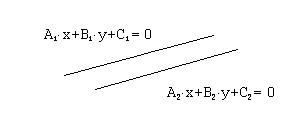
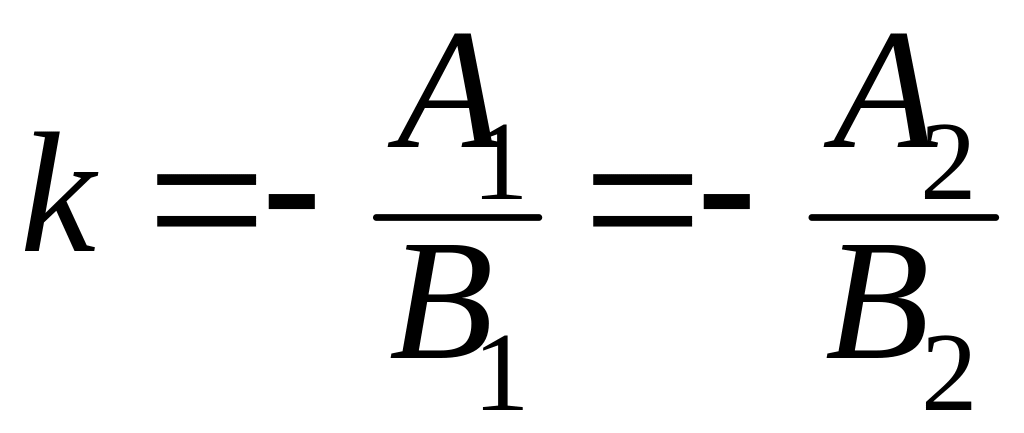. Отсюда получим условие параллельности: .

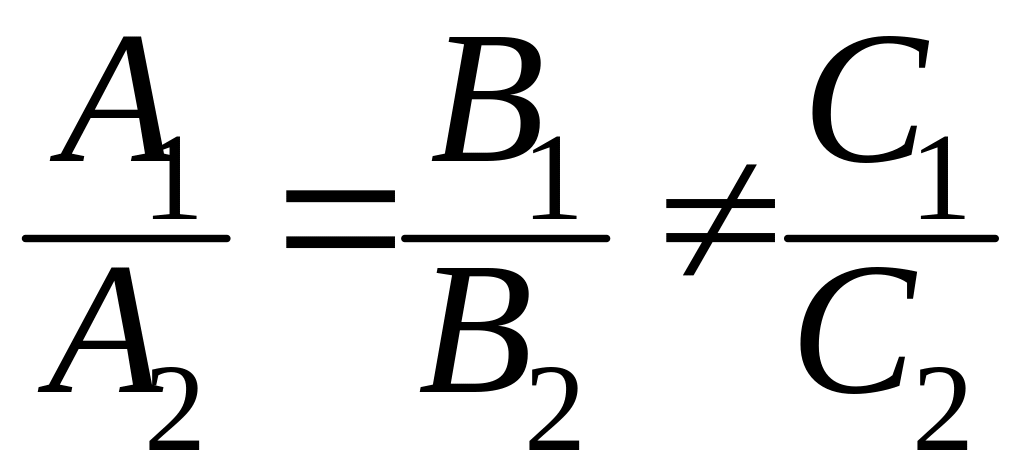В случае 3) угловые коэффициенты прямых разные, то есть, 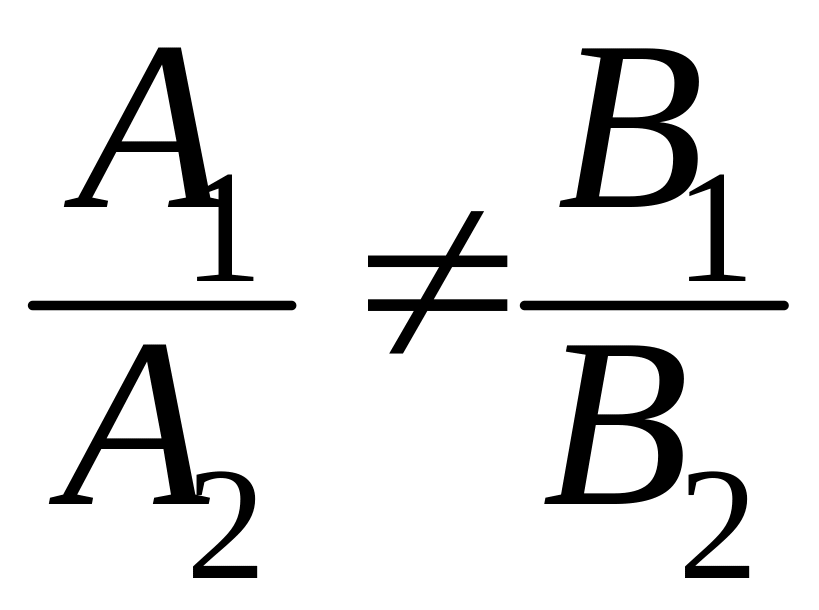, и

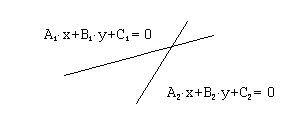
следовательно, прямые пересекаются в одной точке.

Найти точку пересечения двух прямых и – это значит, найти решение системы

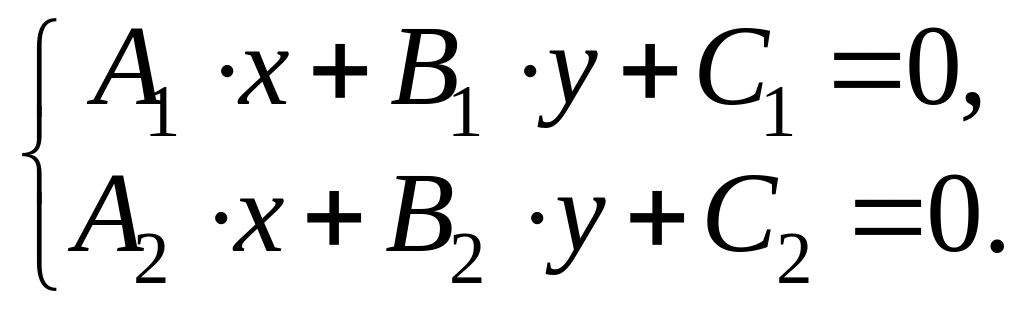
Случай означает, что и главная матрица системы, и расширенная матрица системы имеют одинаковый ранг 1. Поэтому, хотя главный определитель системы равен нулю, система разрешима и имеет бесконечное множество решений.

Случай означает, что главный определитель системы равен нулю, при этом главная матрица системы имеет ранг 1, а расширенная матрица системы имеет ранг 2, поэтому система не имеет решений.

Случай означает, что главный определитель системы отличен от нуля, и следовательно, единственное решение системы можно найти, например, с помощью правила Крамера.

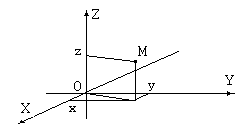
Точка в пространстве XYZ задается уже тремя декартовыми координатами , которые являются проекциями точки на соответствующие оси координат.

Простейшей из пространственных поверхностей является плоскость – геометрическое место таких точек, что отрезок, соединяющий любые две из них, перпендикулярен данному вектору, называемому нормалью к плоскости.

Зададим плоскость с данной нормалью с помощью точки с координатами , лежащей в этой плоскости.

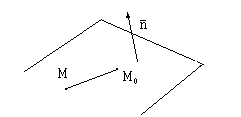
Если взять произвольную, отличную от , точку M с координатами в данной плоскости, то согласно определению и условию взаимной перпендикулярности двух векторов (скалярное произведение этих векторов равно нулю) имеем . Используя координаты этих векторов получим условие взаимной перпендикулярности в виде .

Последнее уравнение и есть уравнение плоскости, проходящей через данную точку. В частности, уравнения плоскостей, параллельных координатным плоскостям, имеют вид , или .