- •Пермь 2012
- •Глава I. Определение геометрических параметров ла 8
- •Глава 2. Динамический анализ ла 16
- •Глава 3. Расчет основных узлов летательного аппарата 18
- •Введение
- •Исходные данные
- •Основные используемые формулы
- •Глава I. Определение геометрических параметров ла
- •1.1 Определение параметров и масс элементов блока I ступени
- •1.2 Определение длины гч и по
- •1.3 Характеристики жрд I ступени
- •Глава 2. Динамический анализ ла
- •Глава 3. Расчет основных узлов летательного аппарата
- •3.1 Расчёт бака окислителя блока 1-й ступени
- •3.2 Расчёт шпангоута подкрепления
- •3.3 Расчёт переходной фермы
- •3.4 Расчет болтового соединения
- •3.5 Расчёт смесительной головки жрд первой ступени
- •3.5.1 Расчёт форсуночного блока
- •3.5.2 Расчёт огневой стенки на срез по контуру
- •3.5.3 Расчёт наружного днища
- •3.6 Расчёт передаточной функции по тангажу
- •Заключение
- •Список литературы
Глава 2. Динамический анализ ла
Исходные данные:
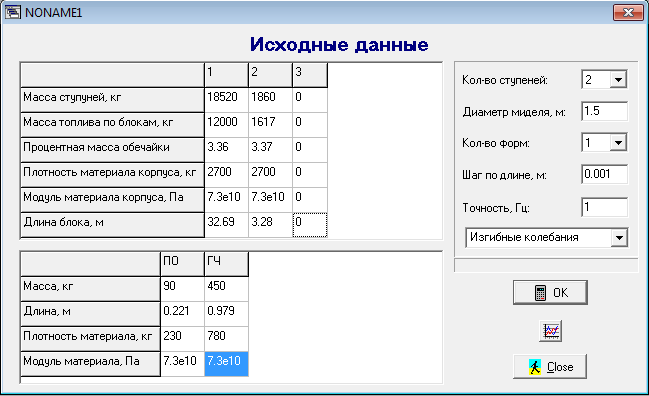
рис. 3
В результате работы программы получили следующие данные:
Изгибные колебания
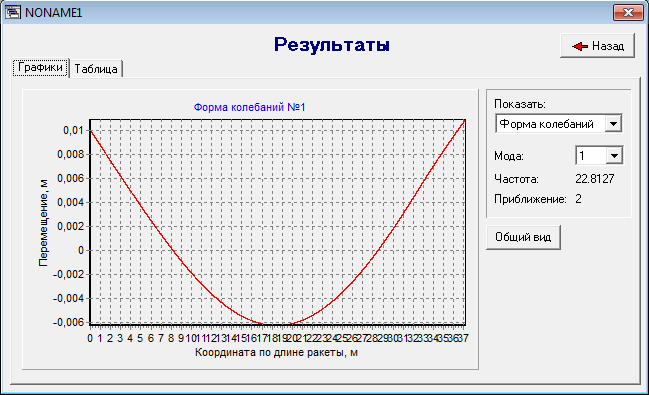
рис. 4
Продольные колебания
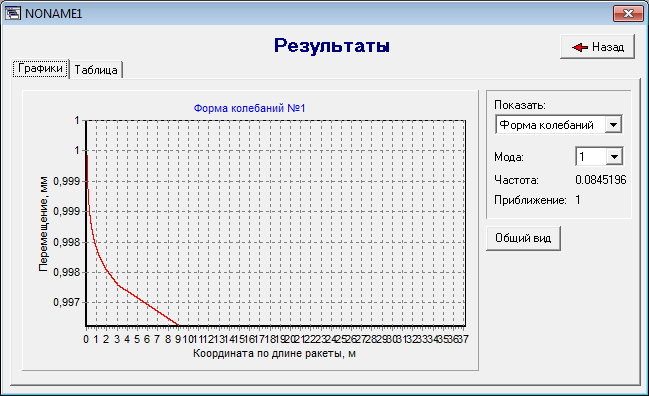
рис. 5
Крутильные колебания
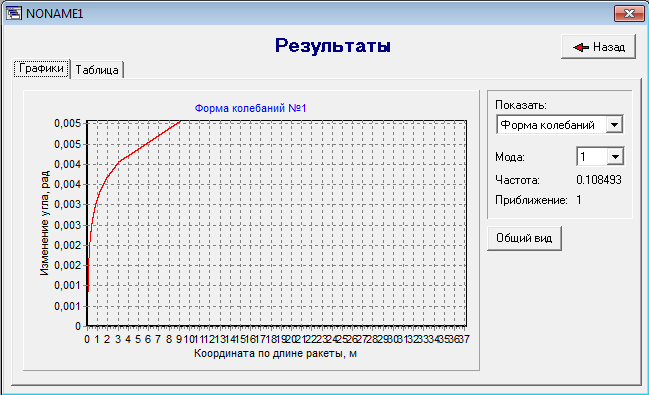
рис. 6
Глава 3. Расчет основных узлов летательного аппарата
3.1 Расчёт бака окислителя блока 1-й ступени
Расчёт бака на устойчивость
Целью расчёта является определение давления наддува p0, которое бы уравновешивало осевые напряжения в обечайке от действия сжимающей силы N и момента M. Расчетная схема представлена на рис. 7
С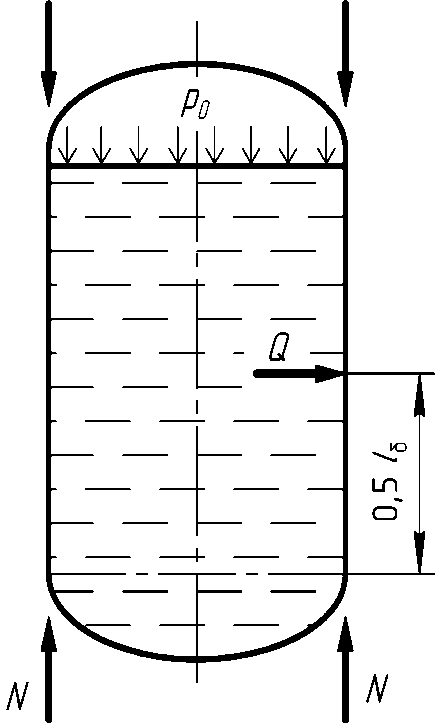 жимающая
сила N:
жимающая
сила N:
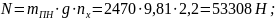
.
Момент M определяется по формуле:
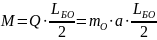
,
где a — наибольшее ускорение жидкости при изгибных колебаниях ЛА
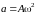
Из расчёта изгибных колебаний
известно, что их частота равна
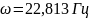 и амплитуда перемещений точки,
соответствующей центру объёма жидкости,
равна
и амплитуда перемещений точки,
соответствующей центру объёма жидкости,
равна
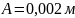 .
Следовательно рис. 7
.
Следовательно рис. 7
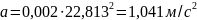
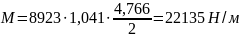
Максимальное значение напряжений сжатия по формуле (13)
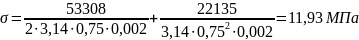
По формуле (15) найдём необходимое давление наддува
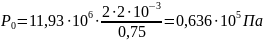
.
3.2 Расчёт шпангоута подкрепления
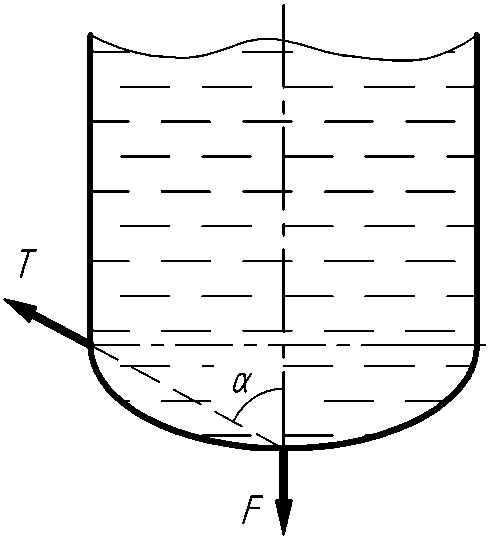
Расчетная схема представлена на рис. 8.
Сила, действующая на днище бака по формуле (16)
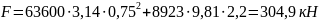
Сила Т будет равна
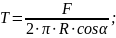 (17)
(17)
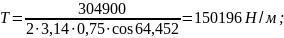
рис. 8
Ш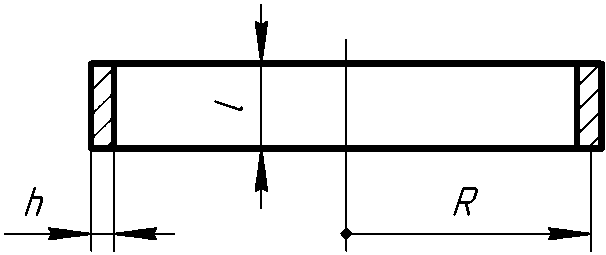 пангоут
подкрепления представляет собой тонкую
цилиндрическую оболочку. геометрические
харакетеристики шпангоута показаны на
рис. 9. Уравнение Лапласа для такой
оболочки имеет вид
пангоут
подкрепления представляет собой тонкую
цилиндрическую оболочку. геометрические
харакетеристики шпангоута показаны на
рис. 9. Уравнение Лапласа для такой
оболочки имеет вид
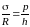 , (18)
, (18)
где:
— внутренние окружные напряжения; рис. 9
h —
толщина оболочки (шпангоута); p —
внешнее давление,
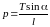 ,
l — высота шпангоута.;
,
l — высота шпангоута.;
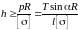 (19)
(19)
Если принять, что высота
шпангоута
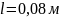 ,
допускаемые напряжения
,
допускаемые напряжения
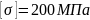 ,
то толщина шпангоута должна быть не
менее:
,
то толщина шпангоута должна быть не
менее:
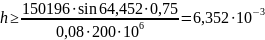
Примем
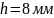 ;
;
.
3.3 Расчёт переходной фермы
С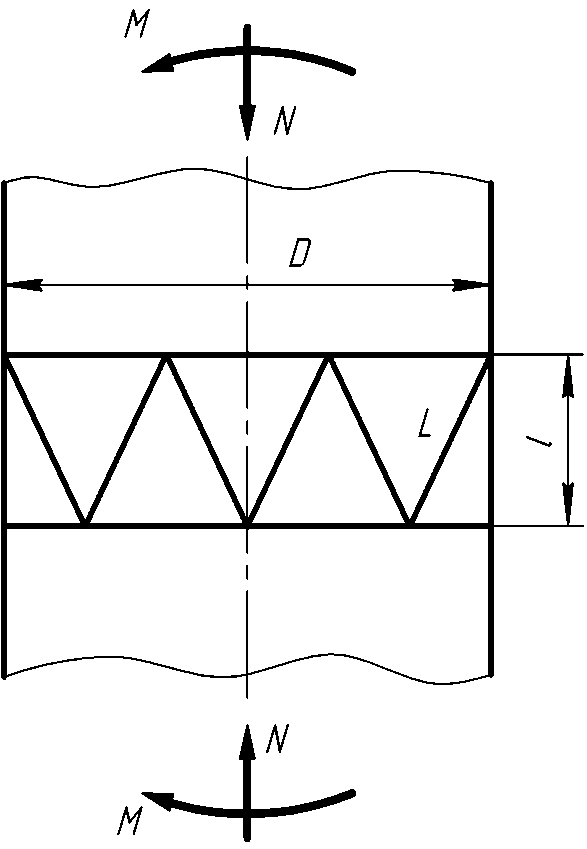 хема
стержневой фермы, соединяющей блоки
1-й и 2-й ступеней, изображена на рисунке
10.
хема
стержневой фермы, соединяющей блоки
1-й и 2-й ступеней, изображена на рисунке
10.
Сжимающая сила N:
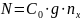 (20)
(20)
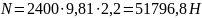
.
Изгибающий момент M определяется по формуле:
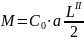 (21)
(21)
наибольшее ускорение при изгибных колебаниях ЛА:
(22)
Из расчёта изгибных колебаний известно, что их частота равна и амплитуда перемещений точки, соответствую-
щей центру масс 2-й ступени,
равна
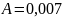 . рис.
10
. рис.
10
Следовательно
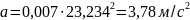
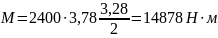
.
Кроме N и M на ферму действует скручивающий момент Mкр, возникающий вследствие крутильных колебаний ЛА:
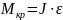 (23)
(23)
где:
J —
момент инерции, для однородного цилиндра
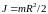 ;
;
 — ускорение вращения,
— ускорение вращения,
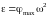
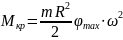 (24)
(24)
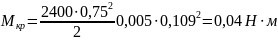
Эквивалентная сила сжатия, возникающая в сечении фермы:
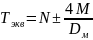 (25)
(25)
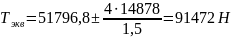
.
Усилие сжатия в стержнях будет равным
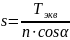 (26)
(26)
,
где:
n — число стержней,
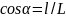 – косинус угла между осью
фермы и осью стержня.
– косинус угла между осью
фермы и осью стержня.
Принимаем
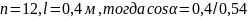
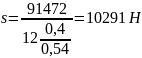
.
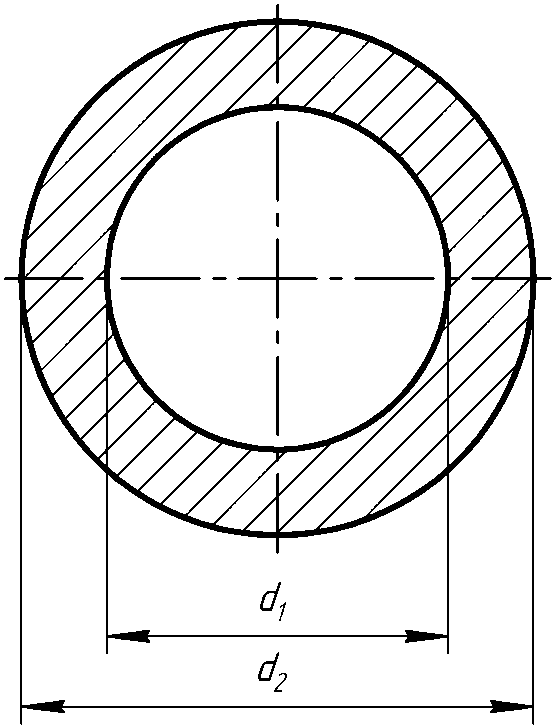
Сечение стержней фермы —
кольцевое (труба, см. рис. 11). Внутренний
и наружный диаметр принимаем равными
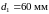 ,
,
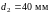 .
Напряжения сжатия в стержнях:
.
Напряжения сжатия в стержнях:
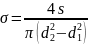 (27)
(27)
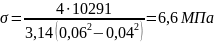
.
Напряжения от действия скручивающего момента: рис. 11
 (28)
(28)
где
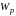 — полярный момент сопротивления сечения
— полярный момент сопротивления сечения
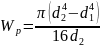 (29)
(29)
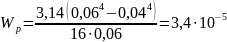
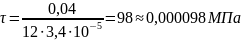
.
Допускаемые напряжения
принимаем равными
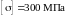 .
.
Эквивалентные напряжения (по IV-й теории прочности):
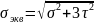 (30)
(30)