Переходные характеристики

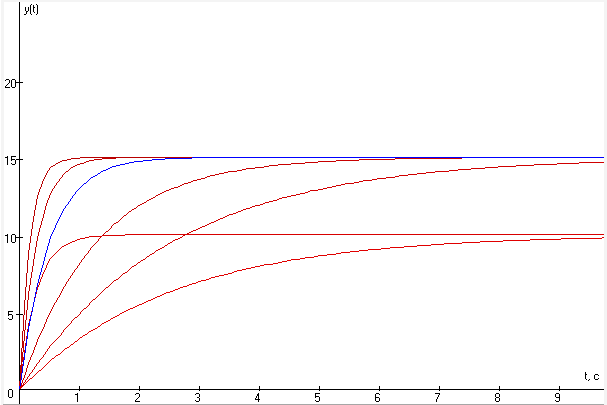
Для каждого графика оцените следующие характеристики:

• установившееся значение выходного сигнала звена и его связь с коэффициентом усиления звена;

1. - y_max(t)=k=10

- t=7.57 с.

- t=2.43 с.

2. - y_max(t)=k=10

- t=0.78 с.

- t=0.23 с.

3. - y_max(t)=k=15

- t=7.57 с.

- t=2.43 с.

4. - y_max(t)=k=15

- t=3.75 с.

- t=1.23 с.

5. - y_max(t)=k=15

- t=0.79 с.

- t=0.23 с.

6. - y_max(t)=k=15

- t=0.5 с.

- t=0.17 с.

7. - y_max(t)=k=15

- t=1.43 с.

- t=0.47 с.

• время, через которое сигнал на выходе звена достигнет 95% от установившегося значения (длительность переходного процесса), связь этого времени с постоянной времени звена;

• При 0.95* ymax(t) t=0.75*T

• время, через которое сигнал на входе звена достигнет 63% от установившегося значения, связь этого времени с постоянной времени инерционного звена.

• При 0.63* ymax(t) t=0.75*T

По результатам исследования переходных характеристик ответьте на следующие вопросы:

• как влияют параметры инерционного звена на характеристики переходного процесса?

• чем больше значение k, тем больше и установившееся значение y(t)

• какова связь между частотными характеристиками инерционного звена и переходными процессами в звене?

• чем меньше значение Т, тем быстрее у(t) достигает установившегося значения.

2. Задание 2. Рассмотрим колебательное звено.

Описание колебательного типового звена

Типовое колебательное звено описывается дифференциальным уравнением второго порядка

((T₁p)² + T₂p + 1)y(t) = kx(t),

где T1,T2 – постоянные времени колебательного звена,

k – коэффициент усиления звена.

Передаточная функция колебательного звена

k

W(p) = ––––––––––––––– ,

(T₁p)² + T₂p + 1

частотная передаточная функция

W(jw) = A(w)e ^jф(w) ,

где k

A(w) = ––––––––––––––––––––––,

((1 - (wT₁)²)² + (wT₂)²)

wT2

ф(w) = - arctg –––––––––– .

1 - (wT₁)²

Особенностью колебательного звена является наличие максимума у зависимости A(w), что свидетельствует о резонансных свойствах звена. Этот максимум зависит от коэффициента демпфирования звена, который определяется соотношением постоянных времени звена

= T₂/2T₁.

С учетом коэффициента демпфирования уравнение звена может быть записано в следующем виде

((T₂p)² + 2Tp + 1)y(t) = kx(t) ,

где T = T₁ – постоянная времени колебательного звена.

Чем меньше коэффициент демпфирования, тем больше максимум усиления звена. При  = 0 колебательное звено превращается в консервативное звено с незатухающими колебаниями. Фазовый угол колебательного звена изменяется в пределах от 0 до -180 при изменении частоты входного сигнала от нуля до бесконечности.

1. Афчх колебательного звена.

Для выполнения исследований частотных характеристик колебательного звена введите его коэффициент усиления k и постоянные времени T₁ и T₂.

Постройте АФЧХ колебательного звена при следующих его параметрах:

Вариант	1	2	3	4	5	6
k	10	10	10	15	15	15
Т1	1.0	1.0	0.1	0.1	1.0	1.0
Т2	1.0	0.5	1	1	0.8	1.0

АФЧХ

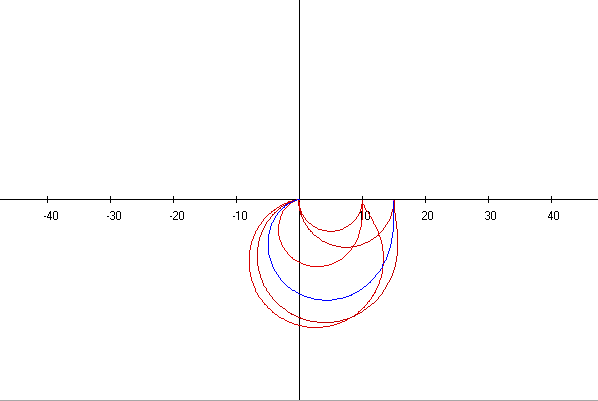
Для каждого графика определите следующие характеристики:

• модуль и фазовый угол АФЧХ на нулевой частоте;

1. При w=0, A=10 φ=0⁰

2. При w=0, A=10 φ=0⁰

3. При w=0, A=10 φ=0⁰

4. При w=0, A=15 φ=0⁰

5. При w=0, A=15 φ=0⁰

6. При w=0, A=15 φ=0⁰

• модуль и фазовый угол на частотах w = 1/T₁ и w = 2/T₁;

1. При w=1/T1=1, A=10 φ=-90⁰

2. При w=1/T1=1, A=20 φ=-90⁰

3. При w=1/T1=10, A=1 φ=-90⁰

4. При w=1/T1=10, A=1,5 φ=-90⁰

5. При w=1/T1=1, A=18,8 φ=-90⁰

6. При w=1/T1=1, A=15 φ=-90 ⁰

1. При w=2/T1=2, A=2.8 φ=-146.3⁰

2. При w=2/T1=2, A=3.2 φ=-161.6⁰

3. При w=2/T1=20, A=0.5 φ=-98.5⁰

4. При w=2/T1=20, A=0.7 φ=-98.5⁰

5. При w=2/T1=2, A=4.4 φ=-151.9⁰

6. При w=2/T1=2, A=4.2 φ=-146.3⁰

• наибольшее значение модуля АФЧХ и частоту, на которой этот максимум наблюдается;

1. kmax=11.5 при w=0.7

2. kmax=20.5 при w=0.9

3. kmax=10.0 при w=0.0

4. kmax=15.0 при w=0.0

5. kmax=20.4 при w=0.8

6. kmax=15.0 при w=0.0

• коэффициент демпфирования звена.

1. ε = T2/2T1

2. ε=0.5

3. ε=0.25

4. ε=5

5. ε=5

6. ε=0.4

7. ε=0.5

По результатам исследования АФЧХ колебательного звена ответьте на следующие вопросы:

• в чем выражается влияние на АФЧХ коэффициента усиления звена k;

• чем больше коэффициент k, тем больше значение амплитуды

• как влияет на АФЧХ постоянная времени T₁ звена;

• значение амплитуды зависит от коэффициента демпфирования. ( x= T2/2T1). Чем больше значение коэффициента, тем меньше амплитуда, и наоборот.

• в чем выражается влияние коэффициента демпфирования;

• Чем больше коэффициент демпфирование, тем более правильной формы петля.

• как зависят усиление звена и его фазовый сдвиг от частоты сигнала.

• Чем меньше Т1 (при неизменном Т)