Государственное общеобразовательное учреждение

Высшего профессионального образования

Омский Государственный Технический Университет

Кафедра автоматизации и робототехники

Отчёт по лабораторной работе № 1

по дисциплине «Теория автоматизированного управления».

Исследование типовых структурных звеньев.

Выполнил: студент гр. А-319

Черещук Екатерина Васильевна

_________________

Проверил: ст. преподаватель каф. АРТ

Лазаренко Ирина Валерьевна

________________

Омск 2011

Лабораторная работа N 1 предусматривает изучение частотных характеристик типовых структурных звеньев и взаимосвязи между видом частотных характеристик и переходными процессами в звеньях. В ходе выполнения лабораторных работ исследуются амплитудно-фазовые частотные характеристики (АФЧХ), логарифмические частотные характеристики (ЛХ) и переходные процессы типовых структурных звеньев. Определяется вид этих характеристик и их взаимная связь.

1. Задание 1. Рассмотрим инерционное звено.

Описание инерционного звена.

Инерционное звено описывается дифференциальным уравнением первого порядка следующего вида

(Tp+1)y(t)=kx(t),

где T – постоянная времени звена,

k – коэффициент преобразования звена,

x, y – входной и выходной сигналы звена,

p – оператор дифференцирования.

Передаточная функция инерционного звена

k

W(p) = –––––– ,

Tp + 1

частотная передаточная функция

W(jw) = A(w)e ^jф(w),

где k

A(w) = ––––––––––––

(1 + (wT)²)

ф(w) = -arctg(wT) .

Годограф W(jw) на комплексной плоскости является амплитудно-фазочастотной характеристикой (АФЧХ) инерционного звена. АФЧХ описывает зависимость коэффициента усиления A(w) звена и угла ф(w) фазового сдвига выходного сигнала звена по отношению ко входному сигналу в случае гармонического входного сигнала.

Частотные свойства инерционного звена можно описать также логарифмической амплитудной характеристикой (ЛАХ)

L(w) = 20lg(A(w))

и логарифмической фазовой характеристикой (ЛФХ)

ф(w) = -arktg(wT).

При построении логарифмических характеристик для оси частот используется логарифмический масштаб, при этом ось частот разбивается на декады – участки, соответствующие десятикратному увеличению частоты. При построении ЛАХ коэффициент преобразования звена выражается в децибелах. Фазовый угол при построении ЛФХ может выражаться как в градусах, так и в радианах. Фазовый угол инерционного звена изменяется в пределах от 0 до -90 при изменении частоты от нуля до бесконечности.

1. Афчх инерционного звена

Введите значение коэффициента усиления k звена и его постоянную времени T₁.

После ввода этих значений выберите в меню График пункт АФЧХ. На экране будет построена АФЧХ инерционного звена. Построения можно повторить при других параметрах инерционного звена, выбрав в меню пункт Параметры. Сравнивая полученные графики можно оценить влияние параметров звена на вид АФЧХ.

Постройте АФЧХ инерционного звена при следующих значениях его параметров:

–

 Вариант  1  2  3  4  5  6 

–

 k  10  50  100  100  100  100 

–

 T₁  1.0  1.0  1.0  0.5  0.1 0.01 

–

АФЧХ

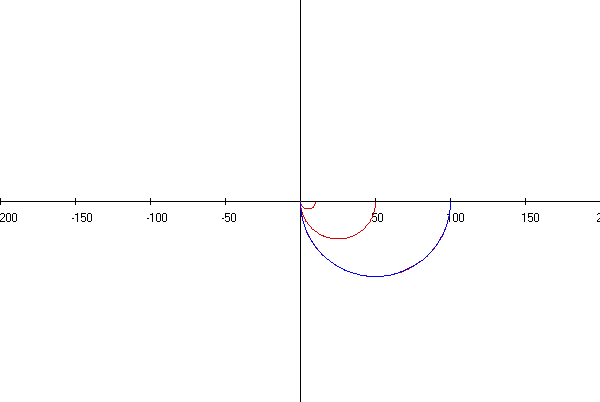
Исследуя построенные графики ответьте на следующие вопросы:

• на какой частоте фазовый сдвиг составляет -45 град. и как эта частота связана с постоянной времени инерционного звена?

1. при φ=-45⁰ и Т=1.0 - ω=1.0.

2. при φ=-45⁰ и Т=0.5 - ω=2.0.

3. при φ=-45⁰ и Т=0.1 - ω=10.0.

4. при φ=-45⁰ и Т=0.01 - ω=100.0.

ω и Т сопряжены (обратно пропорциональная зависимость)

• каков коэффициент усиления звена на частоте фазового сдвига -45 град. и его доля от начального коэффициента усиления?

1. при φ=-45⁰ и k₀=100, k_φ=70

2. при φ=-45⁰ и k₀=50, k_φ=35.4

3. при φ=-45⁰ и k₀=10, k_φ=7.1,

• каков коэффициент усиления звена и его фазовый сдвиг на частоте в пять раз превышающей частоту фазового сдвига -45 град.?

1. ω=5, при этом А=2 , φ=-78.7⁰ (при k=10)

2. ω=5, при этом А=9.8 , φ=-78.7⁰ (при k=50)

3. ω=5, при этом А=19.6 , φ=-78.7⁰ (при k=100

• что происходит с коэффициентом усиления звена и углом фазового сдвига при росте частоты сигнала?

• При росте ω, k уменьшается, а угол растет

(изменяется от 0⁰ до - 90⁰)

2. Логарифмические характеристики инерционного звена.

Если при очередном запросе программы о повторении построений АФЧХ дать отрицательный ответ (нажатием клавиши Enter), то программа перейдет к построению логарифмических характеристик звена. Для первого построения будут использованы параметры звена, заданные при последнем вводе данных (k=100, T=0.01).

ЛАХ и ЛФХ строятся на одном графике, при этом график ЛФХ располагается

под графиком ЛАХ. Отрицательные значения фазовых углов откладываются вверх по

вертикальной оси, при этом угол -180 град соответствует горизонтальной оси графиков.

Постройте логарифмические характеристики инерционного звена при следующих параметрах:

Вариант	1	2	3	4	5	6
k	100	100	100	100	50	10
Т	0.005	0.01	0.1	1.0	0.1	0.1

ЛАХ

Для каждого графика определите коэффициент усиления и фазовый

сдвиг на частоте сигнала w1 = 1/T, а также на частотах 10w1 и 0,1w1. Определите частоту среза wс (частота среза - частота сигнала, на которой коэффициент усиления равен единице). Определите фазовый сдвиг на частоте среза.

		k	φ
0.1w	20	40	-5.8
w	200	36.9	-45.4
10w	2000	19.8	-84.4
wc	17920	1

		k	ф
0.1w	10	40	-5.7
w	100	37	-45.0
10w	1000	20	-84.3
wc	8844	1

		k	φ
0.1w	1	40	-5.7
w	10	37	-45.0
10w	100	20	-84.3
wc	884	1

		k	φ
0.1w	0.1	40	-5.7
w	1	37	-45.0
10w	10	20	-84.3
wc	88.4	1

		k	φ
0.1w	1	33.9	-5.7
w	10	31	-45.0
10w	100	13.9	-84.3
wc	450	1

		k	φ
0.1w	1	20	-5.7
w	10	17	-45.0
10w	100	0	-84.3
wc	88.4	1

По результатам исследования логарифмических характеристик:

• ответьте на вопросы, поставленные в предыдущем исследовании.

1. при φ=-45⁰ и Т=0,005 - ω=200,0.

2. при φ=-45⁰ и Т=0,01 - ω=100,0.

3. при φ=-45⁰ и Т=0,1 - ω=10,0.

4. при φ=-45⁰ и Т=1,0 - ω=1,0.

ω и Т сопряжены (обратно пропорциональная зависимость)

• при φ=-45⁰ и k₀=100, L(w)=37 A(w)=70.79

при φ=-45⁰ и k₀=50, L(w)=31 A(w)=70.79

• ω=5, при этом А=9.77 , φ=-78.7⁰ (при k=50)

ω=5, при этом А=19.72 , φ=-78.7⁰ (при k=100)

• При росте ω, k уменьшается, а угол растет

(изменяется от 0⁰ до - 90⁰)

• определите как влияют параметры звена на частоту среза его частотной характеристики?

• при изменении k изменяется и значение амплитуды (прямая зависимость). k определяет максимальное значение амплитуды A(w) и следовательно L(w).

• определите связь АФЧХ с логарифмическими частотными характеристиками.

• при изменении постоянной времени Т изменяется значение частоты (обратная зависимость) Чем больше Т, тем больше и частота среза wc .

3. Переходные характеристики инерционного звена.

Постройте переходные характеристики звена при следующих его параметрах:

Вариант	1	2	3	4	5	6	7
k	10	10	15	15	15	15	15
Т	1.0	0.1	1.0	0.5	0.1	0.005	0.011