1) Совместными 2) зависимыми

3) Независимыми 4) несовместными

Р Е Ш Е Н И Е

Ясно, что эти события совместны и независимы.

О Т В Е Т: 1, 3.

30 Если случайные события А и В независимы, то р(АВ)=р(А)р(В) (вероятность произведения равна произведению вероятностей); если А и В – зависимые, то р(АВ)=р(А)∙р(В/А), где р(В/А) – условная вероятность (вероятность появления события В при условии, что событие А наступило)

ЗАДАНИЕ №30 (выберите один вариант ответа)

По оценкам экспертов вероятности банкротства для двух предприятий, производящих разнотипную продукцию 0,2 и 0,35. Тогда вероятность банкротства обоих предприятий равна...

ВАРИАНТЫ ОТВЕТОВ:

1) 0,07 2) 0,55

3) 0,7 4) 0,52

Р Е Ш Е Н И Е

Здесь надо найти вероятность произведения (совместного осуществления) двух независимых событий = р(АВ)=р(А)р(В)=0,2∙0,35=0,07.

О Т В Е Т: 1.

31 Если событие А может наступить при условии одного из нескольких событий, образующих полную группу событий, то вероятность р(А) вычисляется по формуле полной вероятности как сумма произведений вероятностей событий, образующих полную группу событий, на условные вероятности появления события А при осуществлении соответствующего события.

Так, например, если событие А может наступить при условии появления трех событий Н₁, Н₂, Н₃, образующих полную группу событий, то р(А)=р(Н₁)∙р(А/Н₁)+р(Н₂)∙р(А/Н₂)+р(Н₃)∙р(А/Н₂).

Если в аналогичных предположениях А наступает при появлении двух событий Н₁, Н₂, то р(А)=р(Н₁)∙р(А/Н₁)+р(Н₂)∙р(А∙Н₂).

ЗАДАНИЕ №31 (выберите один вариант ответа)

Событие А может наступить лишь при условии появления одного из двух несовместных событий В₁ и В₂, образующих полную группу событий.

Известны вероятность Р(В₁)= и условные вероятности Р(А/В₁)= , Р(А/В₂)= .

Тогда вероятность Р(А) равна...

ВАРИАНТЫ ОТВЕТОВ:

1) 2)

3) 4)

Р Е Ш Е Н И Е

В данном случае В₁ и В₂ – противоположные события. Поэтому р(В₂)=1-р(В₁)=1- .

Применим формулу полной вероятности:

р(А)=р(В₁)∙р(А/В₁)+р(В₂)∙р(А/В₂)= ∙

О Т В Е Т: 3.

32 Если у=f(x) является плотностью распределения случайной величины, то . Геометрический смысл этого условия состоит в следующем: площадь, лежащая под графиком функции y=f(x), равна 1.

ЗАДАНИЕ №32 (выберите один вариант ответа)

График плотности распределения вероятностей f(x) случайной величины приведен на рисунке

у у=f(x)

а

0 0,5 1 х

Тогда значение a равно...

ВАРИАНТЫ ОТВЕТОВ:

1) 2) 1,2

3) 0,9 4)

Р Е Ш Е Н И Е

Площадь, лежащая под графиком функции у=f(x), равна сумме площадей прямоугольника и треугольника ( ), т.е. S=0,5a+0,25a=1 или 0,75а=1, откуда а= .

ОТВЕТ: 1.

33 Для изучения выборки строят для нее статистический ряд. Это таблица, в первой строке которой перечислены наблюдаемые значения случайной величины, а во второй соответствующие частоты наблюдаемых значений.

x_i x₁ x₂ ….. x_k

n_i n₁ n₂ ….. n_k

Очевидно, что , где n – объем выборки.

ЗАДАНИЕ №33 (выберите один вариант ответа)

Из генеральной совокупности извлечена выборка объема n=50:

xi	1	2	3	4
ni	10	n2	8	7

Тогда n₂ равен...

ВАРИАНТЫ ОТВЕТОВ:

1) 26 2) 25

3) 9 4) 50

Р Е Ш Е Н И Е

Сумма частот 10+n₂+8+7 будет равна n=50 при n₂=25.

О Т В Е Т: 2.

34 Выборочная дисперсия D_B является смещенной оценкой генеральной дисперсии. Исправленная дисперсия S² определяется по формуле , где n-объем выборки.

Оценка S² является несмещенной оценкой для генеральной дисперсии.

ЗАДАНИЕ №34 (выберите один вариант ответа)

Для выборки объема n=10 вычислена выборочная дисперсия D_B=180, исправленная дисперсия S² для этой выборки равна...

ВАРИАНТЫ ОТВЕТОВ:

1) 324 2) 200

3) 162 4) 400

Р Е Ш Е Н И Е

Имеем

О Т В Е Т: 2.

3 5 Выборочный коэффициент корреляции r_B по модулю не превосходит 1, т.е. . Если в уравнении регрессии у=ах+b коэффициент а>0, то r_B>0; если же а<0, то r_B<0.

ЗАДАНИЕ №35 (выберите один вариант ответа)

Выборочное уравнение парной регрессии имеет вид у=4,4-2,2х. Тогда выборочный коэффициент корреляции может быть равен...

ВАРИАНТЫ ОТВЕТОВ:

1) 4,4 2) 0,9

3) -0,9 4) 0,5

Р Е Ш Е Н И Е

Здесь коэффициент при х меньше нуля, поэтому r_B<0.

О Т В Е Т: 3.

Если бы этот коэффициент был больше нуля, то верными были бы ответы 2 и 4 (числа 0,9 и 0,5 меньше 1). Ответ 1 неверный, так как 4,4>1.

3 6 Статистической называют гипотезу о виде неизвестного распределения или о параметрах известных распределений. Выдвинутую гипотезу называют основной (нулевой) и обозначают Н₀. Конкурирующей (альтернативной) называют гипотезу Н₁, которая противоречит нулевой гипотезе H₀. Например: Н₀:а=10, Н₁:а 10.

ЗАДАНИЕ №36 (выберите один вариант ответа)

Если основная гипотеза имеет вид Н₀: а=9, то конкурирующей может быть гипотеза...

ВАРИАНТЫ ОТВЕТОВ:

1) Н₁: а 8 2) Н₁: а 9

3) Н₁: а<9 4) Н₁: а 9

Р Е Ш Е Н И Е

Ясно, что гипотезы ответов 2 и 4 не противоречат Н₀. Гипотеза ответа 1 – просто другая гипотеза, а гипотеза ответа 3 противоречит гипотезе Н₀.

О Т В Е Т: 3.

37 В признаках делимости включают делимость на взаимно простые множители.

ЗАДАНИЕ №37 (выберите один вариант ответа)

Необходимым и достаточным условием делимости натурального числа N на 60 является его делимость...

ВАРИАНТЫ ОТВЕТОВ:

1) на 2, на 10 и на 3 2) на 6 и на 10

3) на 3, на 4 и на 5 4) на 2 и на 30

Р Е Ш Е Н И Е

В ответе 3 множители 3, 4, 5 являются взаимно простыми.

О Т В Е Т: 3.

Например, число 90 делится на 2, 10 и 3 (см. отв.1), но не делится на 60; оно также делится на 6, 10 (см.отв.2), но не делится на 60; это число делится на 2, 30 (см.отв.4), но не делится на 60.

38 -окрестность точки (числа) х=а является интервал . Ясно, что

ЗАДАНИЕ №38 (выберите несколько вариантов ответа)

-окрестность точки (числа) х= -4 может принадлежать множеству...

ВАРИАНТЫ ОТВЕТОВ

1) (-5;-4]U(-4;-3) 2) (-6; -2) \ [-4; 0)

3) (-5; -3) (-4; -2) 4) (-6; -2)\ [-3;-1)

Р Е Ш Е Н И Е

На числовой оси построим множество ответа 2, оно состоит из тех точек интервала (-6; -2), которые не принадлежат интервала [-4; 0), т.е. х=4 множеству ответа 2 не принадлежит.

В ответе 3 надо найти пересечение интервалов (-5; -3) и (-4;-2):

-5 -4 -3 -2 0

Число х = -4 этому множеству не принадлежит. Таким образом ответы 2 и 3 неверны.

Для ответа 1 построим объединение промежутков (-5; -4] и (-4; -3). Здесь (-5; -4] U(-4; -3)=

=(-5; -3). Число х=-4 (-5; -3). Ответ 1 – верный.

Для ответа 4 построим множество (-6;-2)\[-3; -1). Для этого из интервала (-6; -2) выбросим те его точки, которые принадлежат промежутку [-3; -1). Из рисунка видно, что

( -6; -2) \ [-3;-1)=(-6; -3). Число х=-4 (-6;-3). Ответ 4 – верный.

-6 -3 -2 -1

О Т В Е Т: 1,4

3 9 Выборки из данных n элементов по k элементов, отличающиеся друг от друга хотя бы одним элементом, называются сочетаниями. Число таких сочетаний обозначают через C^k_n и вычисляют по формуле

C^k_n= .

Выборки из данных n элементов по k элементов, отличающиеся друг от друга хотя бы одним элементом либо их порядком, называют размещениями. Число таких размещений обозначают через и вычисляют по формуле =n(n-1)(n-2)…..[n-(k-1)].

Размещения из данных n элементов по n элементов называют перестановками (они отличаются лишь порядком элементов). Число перестановок из n элементов обозначают через Р_n. Ясно, что (n-факториал).

ЗАДАНИЕ №39 (выберите один вариант ответа)

Число всевозможных способов, которыми можно извлечь из 6 различных учебников 3, равно...

ВАРИАНТЫ ОТВЕТОВ:

1) 18 2) 20

3) 120 4) 12

Р Е Ш Е Н И Е

Здесь способы отличаются друг от друга только составом выборки, то есть надо подсчитать .

О Т В Е Т: 2.

40 На рисунке изображен граф с вершинами А, В, С, D и Е.

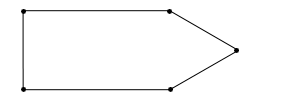
А В Ребрами графа являются пути, которые

Е соединяют вершины графа.

С D Перечислим их: (А,В), (А,С), (В,Е),

(С,D), (D,Е), (Е,Е).

ЗАДАНИЕ №40 (выберите варианты согласно тексту задания)

Неориентированные графы имеют множество вершин {A, B, C, D}. Множества их ребер заданы отношением инцидентности: каждое ребро представлено как пара вершин. Поставьте в соответствии каждому графу его графическое изображение.

1) {(A,C), (B,C), (C,D),(B,D)}

2) {(A,B), (A,C), (B,C), (C,D)}

3) {(A,C), (B,C), (B,D), (B,B)}

ВАРИАНТЫ ОТВЕТОВ:

А В A B

а) b)

С D C D

A B A B

c) d)

C D C D

A B

e)

C D

Р Е Ш Е Н И Е

Сравним перечень ребер с графиками.

1. Ребра (А,С) нет на графе а); оно есть на графе в).

Следующее ребро (В,С) есть на граве в), но на этом графе нет ребра (С,D), т.е. для первого случая ответы а) и b) неверные.

Ответ с) тоже неверен (нет ребра (В,С); ответ е) тоже не соответствует перечню ребер. На рисунке d) представляет граф с ребрами (А,С), (В,С), (С,D),(B,D).

О Т В Е Т: d.

2. В этом случае ребра (А,В) нет на рисунках а,b,c,d. Рисунок е) соответствует этому перечню ребер.

О Т В Е Т: е.

3. Ребро (В,В) имеется на графах в) и е). Сопоставляя эти графы с ребрами (А,С), (В,С) и (В,D) убеждаемся, что верный ответ для этого случае – граф в).

О Т В Е Т: в.

С О Д Е Р Ж А Н И Е

Предисловие...................................................................................3

Задания 1-4 (линейная алгебра)................................................... 6

Задания 5-8 (абстрактная алгебра)............................................ 11

Задания 9-12 (аналитическая геометрия)..................................14

Задания 13-16 (дифференциальная геометрия)........................18

Задания 17-20 (математический анализ)...................................21

Задания 21-24 (комплексный анализ)........................................26

Задания 25-28 (дифференциальные уравнения).......................30

Задания 29-32 (теория вероятностей)........................................35

Задания 33-36 (математическая статистика)............................39

Задания 37-40 (дискретная математика)...................................42

Содержание..................................................................................48