
- •А. М. Капустин, м. В. Кокшаров, а. П. Стариков Гидравлика Омск 2007
- •1.1. Основные теоретические сведения
- •1.2. Жидкостные манометры
- •1.3. Пружинные приборы
- •Лабораторная работа 2
- •2.1. Основные теоретические сведения
- •2.2. Описание лабораторной установки
- •2.3. Порядок проведения опыта и вычислений
- •3.1. Основные теоретические сведения
- •3.2. Описание лабораторной установки
- •3.3. Порядок проведения опыта и вычислений
- •4.1. Основные теоретические сведения
- •4.2. Описание лабораторной установки
- •4.3. Порядок проведения опыта и вычислений
- •5.1. Основные теоретические сведения
- •5.2. Описание лабораторной установки
- •5.3. Порядок проведения опытов и вычислений
- •6.1. Основные теоретические сведения
- •6.2. Описание лабораторной установки
- •6.3. Порядок проведения опытов и вычислений
- •7.1. Основные теоретические сведения
- •7.2. Описание лабораторной установки
- •7.3. Порядок проведения опыта и вычислений
- •8.1. Основные теоретические сведения
- •8.2. Описание лабораторной установки
- •8.3. Порядок проведения опыта и вычислений
- •Учебное издание Капустин Александр Михайлович,
- •Редактор т. С. Паршикова
- •6 44046, Г. Омск, пр. Маркса, 35
5.1. Основные теоретические сведения
При движении жидкости по трубопроводу часть ее энергии тратится на преодоление сопротивления по длине. Потери энергии рассчитываются по формуле:
|
(18) |
где λ – коэффициент сопротивления трения по длине;
l – длина трубопровода, м;
d – диаметр трубопровода, м;
v – средняя скорость жидкости, м/с.
Теоретически коэффициент сопротивления λ можно рассчитать только для ламинарного режима. Для турбулентного режима определяется опытным путем и для его расчета используют экспериментальные данные.
Коэффициент сопротивления λ является безразмерной переменной величиной, зависящей от ряда характеристик: диаметра трубы, шероховатости ее стенок, вязкости и скорости жидкости. Влияние указанных характеристик проявляется по-разному при различных режимах движения жидкости. В одном диапазоне значений числа Re на коэффициент λ влияет в большей степени скорость жидкости, в другом – геометрические характеристики – диаметр и шероховатость трубы. Буквой kэ принято обозначать значение эквивалентной шероховатости. Под эквивалентной шероховатостью понимают такую высоту выс-тупов шероховатости, образованной из песчинок одинаковых размеров (шероховатость Никурадзе), которая дает при расчетах одинаковое с заданной шероховатостью значение коэффициента сопротивления λ. Таким образом, kэ трубопроводов определяется не прямыми измерениями высоты выступов, а с по-мощью гидравлических испытаний.
В зависимости от числа Re коэффициент λр рассчитывается по формулам:
|
Re < 2320, λр = 64 / Re; |
(19) |
|
4,5∙103 < Re < 105, λр = 0,3164 / Re0,25; |
(20) |
|
105 < Re < 3∙106, λр = 0,032 + 0,221 / Re0,237. |
(21) |
При турбулентном режиме для определения коэффициента часто используется универсальная формула (формула Альтшуля):
|
(22) |
5.2. Описание лабораторной установки
Работа выполняется на стенде гидравлическом универсальном ТМЖ-2 с модулем 1. Модуль представляет собой трубу диаметром 0,015 м (рис. 15), на которой выделен участок длиной 0,3 м. Потеря напора на участке определяется по показаниям пьезометров. Расход жидкости измеряется с помощью ротаметра.

Рис. 15. Схема лабораторной установки
5.3. Порядок проведения опытов и вычислений
Подготовить стенд ТМЖ-2 к работе: включить насос и освободить напорный бак от воздуха.
Установить минимальный расход жидкости и измерить его с помощью ротаметра.
Зафиксировать показания пьезометров и записать их в табл. 5.
По результатам измерений рассчитать потерю напора, среднюю скорость, коэффициент сопротивления, число Рейнольдса.
Данные расчетов занести в табл. 5.
Построить график зависимости λэ = λ(Re).
Для получения зависимости λэ = λ(Re) следует выполнить не менее 8 – 10 опытов при разных расходах жидкости.
Построенный график λэ = λ(Re) наложить на график Никурадзе и сделать вывод о зоне сопротивления, в которую попали опытные точки и значение относительной эквивалентной шероховатости kэ.
По полученным числам Re подобрать формулу и определить расчетные значения λр. Сравнить экспериментальные и расчетные значения коэффициентов сопротивления.
Таблица 5
Результаты измерений и расчета значения коэффициента сопротивления прямого участка трубы
Показатель |
Номер опыта |
|||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Пьезометрический
напор в сечении 1
|
|
|
|
|
|
|
|
|
Пьезометрический
напор в сечении 2
|
|
|
|
|
|
|
|
|
Потеря напора (hp = h1 – h2), м |
|
|
|
|
|
|
|
|
Расход жидкости Q, м3/с |
|
|
|
|
|
|
|
|
Средняя скорость жид-кости , м/с |
|
|
|
|
|
|
|
|
Коэффициент
сопротивления
|
|
|
|
|
|
|
|
|
Число Рейнольдса
|
|
|
|
|
|
|
|
|
Температура воды Т, °С |
|
|
|
|
|
|
|
|
Коэффициент кинематической вязкости ν, м2/с |
|
|
|
|
|
|
|
|
Относительная эквивалентная шероховатость kэ/d |
|
|
|
|
|
|
|
|
Расчетное значение λр |
|
|
|
|
|
|
|
|
Лабораторная работа 6
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА МЕСТНОГО
СОПРОТИВЛЕНИЯ ПРИ ВНЕЗАПНОМ РАСШИРЕНИИ ПОТОКА
Цель работы: экспериментальным путем определить значение коэффициента местного сопротивления в.р и найти его зависимость от числа Рейнольдса в потоке.

 ,
, .
.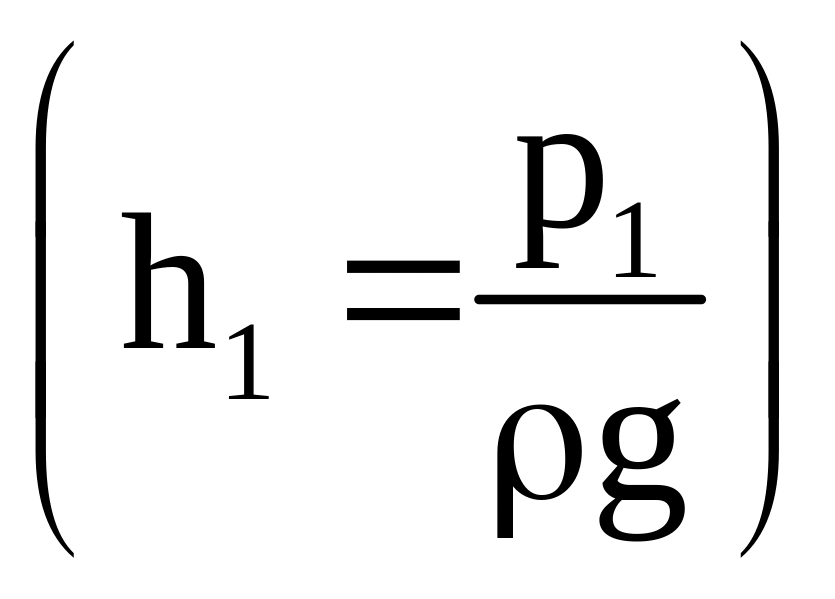 ,
м
,
м ,
м
,
м
